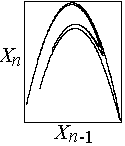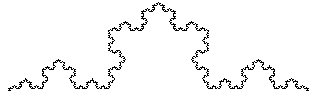Fractals

Comments on Homework #9 (Autocorrelation Function)

• There was a certain confusion about the notation
• The autocorrelation function of Lorenz is ~ 6 x 0.05 = 0.3 seconds

Review (last week) - Nonlinear Prediction and Noise Reduction

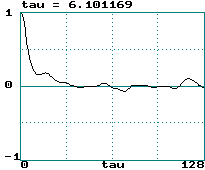
• Autocorrelation Function
• g(n) = S (X_i - X_av)(X_i+n - X_av) / S (X_i - X_av)²
• Correlation time is width of g(n) function (call it tau)
• tau can be taken as the value of n for which g(n) = 1/e = 37%
• 0.5/tau is sometimes called a "poor-man's Lyapunov exponent"
• From the correlation function g(n), the power spectrumP(f) can be found:

P(f) = 2 S g(n) cos(2pfnDt) Dt  (ref: Tsonis)
• Time-Delayed Embeddings
• (Almost) any variable(s) can be analyzed
• Create multi-dimensional data by taking time lags
• May need up to 2m + 1 time lags to avoid intersections

where m is the dimension of solution manifold
• Must choose an appropriate D_E (embedding dimension)
• Increase D_E until topology of attractor (dimension) stops changing
• Or use the method of false nearest neighbors
• Must choose an appropriate Dt for sampling a flow
• Rule of thumb:  Dt ~ tau / D_E
• A better method is to use minimum mutual information (see Abarbanel)
• Summary of Important Dimensions
• Configuration (or state) space (number of independent dynamical variables)
• Solution manifold (the space in which the solution "lives" - an integer)
• Attractor dimension (fractional if it's a strange attractor)
• Kaplan-Yorke (Lyapunov) dimension
• Hausdorff dimension
• Cover dimension
• Similarity dimension (see below)
• Capacity dimension (see below)
• Information dimension
• Correlation dimension (next week)
• ... (infinitely many more)
• Observable (1-D for a univariate (scalar) time series: X_i)
• Reconstructed (time-delayed) state space (can be chosen arbitrarily)
• Time-delayed embedding (the minimum time-delayed state space that preserves the topology of the solution)

Nonlinear Prediction

• There are many forecasting (prediction) methods
• Conventional linear prediction methods apply in the time domain
• Fit the data to some function of time and evaluate it
• The function of time may be nonlinear
• The dynamics are usually assumed to be linear
• Linear equations can have oscillatory or exponential solutions
• Nonlinear methods usually apply in state space
• Example (predicting next term in Hénon map - HW # 11):
• We know X_n+1 = 1 - CX_n² + BX_n-1
• In a 2-D embedding, the next value is unique


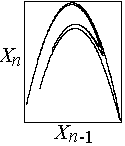
• Find M nearest points in X_n-X_n-1 space
• Calculate their average displacement:  DX = <X_n+1 - X_n>
• Use DX to predict next value in time series
• Repeat as necessary to get future time steps
• Sensitive dependence will eventually spoil the method
• Method does not necessary keep you on the attractor (but could be modified to do so)
• Growth of prediction error crudely gives the Lyapunov exponent
• Example (Hénon map average error):


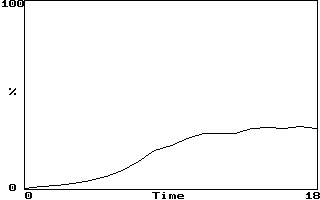
• If LE = 0.604 bits/iterations, error should double every 1.7 iterations
• Saturation occurs after error grows sufficiently
• Prediction methods can also remove some noise
• Predict all points not just next point
• Can be used to produce an arbitrarily long time series
• This is useful for calculating LE, dimension, etc.
• Gives an accurate answer to an approximate model
• Example:  Hénon map with noise, removed using SVD
• Need to choose D_E and M optimally
• Alternate related method is to construct f(X_n, X_n-1, ...)
• This improves noise reduction but is less accurate
• The solution can eventually walk off the attractor
• Best method is to make a local function approximation
• Usually linear or quadratic functions are used
• This offers best of both worlds but is hard to implement and slow
• Case study - 20% drop in S&P500 on 10/19/87 ("Black Monday')
• Could this drop have been predicted?
• Consider 3000 previous trading days (~ 15 years of data)
• Note that the 20% drop was unprecedented
• Three predictors:
• Linear (ARMA)
• Principle component analysis (PCA or SVD)
• Artificial neural net (essentially state-space averaging)
• The method above predicts a slight rise (not shown)
• The stock market has little if any determinism

Lyapunov Exponent of Experimental Data

• We previously calculated largest LE from known equations
• Getting the LE from experimental data is much more difficult (canned routines are recommended - See Wolf)
• Finding a value for LE may not be very useful
• Noise and chaos both have positive LEs (LE = infinity for white noise)
• Quasi-linear dynamics have zero LE, but there are better ways to detect it (look for discrete power spectrum)
• Inpossible to distinguish zero LE from very small positive LE
• The value obtained is usually not very accurate
• Conceptually, it's easy to see what to do:
• Find two nearby points in a suitably chosen embedding D_E
• Follow them a while and calculate <log(rate of separation)>
• Repeat with other nearby points until you get a good average
• There are many practical difficulties:
• How close do the points have to be?
• What if they are spuriously close because of noise?
• What if they are not oriented in the right direction?
• How far can they safely separate?
• What do you do when they get too far apart?
• How many pairs must be followed?
• How do you choose the proper embedding?
• It's especially hard to get exponents other than the largest
• The sum of the positive exponents is called the entropy

Hurst Exponent (skip this if time is short)

• Consider a 1-D random walk
• Start at X₀ = 0
• Repeatedly flip a (2-sided) coin (N times)
• Move 1 step East on heads
• Move 1 step West on tails
• <X> = 0,  <X²> = N after N steps of size 1
• Proof:
• N = 1:  E = 1, W = 1, <X²> = 1
• N = 2:  EE = WW = 2, EW = WE = 0, <X²> = 2
• N = 3:  EEE = WWW = 3, other 6 = 1, <X²> = 3
• etc...  <X²> = N
• Numerically generated random walk (2000 coin flips):


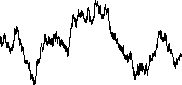
• Extend to 2-D random walk
• Start at R₀ = 0  (X₀ = Y₀ = 0)
• Repeatedly flip a 4-sided coin (N times)
• Move 1 step N, S, E, or W respectively
• <R> = 0,  <R²> = N after N steps of size 1
• Animation shows R_rms = <R²>^1/2 = (DR)t^1/2
• Result is general
• Applies to any dimension
• Applies for any number of directions (if isotropic)
• Applies for any step size (even a distribution of sizes)
• However, coin flips must be uncorrelated ("white")
• H = 1/2 is the Hurst exponent for this uncorrelated random walk
• H > 1/2 means positive correlation of coin flips (persistence)
• H < 1/2 means negative correlation of coin flips (anti-persistence)
• The time series X_n has persistence for H > 0
• Note ambiguity in definition of Hurst exponent
• The steps are uncorrelated (white)
• The path is highly correlated (Brownian motion)
• Can get from one to the other by integrating or differentiating
• I prefer to say Hurst exponent of white noise is zero,

and brown noise (1/f ²) is 0.5, but others disagree
• With this convention, H = a/4 for 1/f ^a noise
• Hurst exponent has same information as power law coefficient
• If power spectrum is not a power law, no unique exponent
• Calculation of Hurst exponent from experimental data is easy
• Choice of embedding not critical  (1-D usually OK)
• Use each point in time series as an initial condition
• Calculate average distance d (= |X - X₀|) versus t
• Plot log(d) versus log(t) and take slope
• Example #1  (Hurst exponent of brown noise):


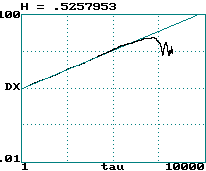
• Example #2  (Hurst exponent of Lorenz x(t) data)

Capacity Dimension

• The most direct indication of chaos is a strange attractor
• Strange attractors will generally have a low, non-integer dimension
• There are many ways to define and calculate the dimension
• We already encountered the Kaplan-Yorke dimension, but it requires knowledge of all the Lyapunov exponents
• Most calculations depend on the fact that amount of "stuff" M scales as d^D where d is the linear size of a "box"
• Hence D = d log(M) / d log(d)  [i.e., D is the slope of log(M) versus log(d)]
• One example is the capacity dimension (D₀)
• Closely related to the Hausdorff dimension or "cover dimension"
• Consider data representing a line and a surface embedded in 2-D
• The number of squares N of size d required to cover the line (1-D) is proportional to 1/d
• The number of squares N of size d required to cover the surface (2-D) is proportional to 1/d²
• The number of squares N of size d required to cover a fractal (dimension D₀) is proportional to 1/d^D0
• Hence the fractal dimension is given by  D₀ = d log(N) / d log(1/d)
• This is equivalent to  D₀ = -d log(N) / d log(d)
• Plot log(N) versus log(d) and take the (negative) slope to get D₀
• More typically D₀ is calculated using a grid of fixed squares
• Example (2000 data points from Hénon map with D_E = 2)
• This derivative should be taken in the limit d --> 0
• The idea can be generalized to D_E > 2 using (hyper)cubes
• Many data points are required to get a good result
• The number required increases exponentially with D₀
• If 10 points are needed to define a line (1-D),

then 100 points are needed to define a surface (2-D),
and 1000 points are needed to define a volume (3-D), etc.

Examples of Fractals

• There are many other ways to make fractals besides chaotic dynamics
• They are worthy of study in their own right
• They provide a new way of viewing the world
• Fractal slide show (another "lecture within a lecture")
• Nature's Fractals
• Snowflake
• Cantor set
• Cantor curtains
• Devil's staircase
• Hilbert curve
• Von Koch island
• Flat Fournier universe
• Weierstrass function  ( x(t) = S[cos(2ⁿt) / 2^(2-D)n] )
• Fractal word
• Sierpinski triangle
• Sierpinski carpet
• Cantor square
• Cantor maze
• Twin dragon
• Julia dendrite  (Z_n+1 = Z_n² + i)
• Fractal fern
• Maple leaf
• Peitgen tree
• Fractal tree
• Diffusion-limited aggregation
• Iterated function systems
• Cellular automata
• Game of life
• Strange attractors
• Mandelbrot set  (Z_n+1 = Z_n² + C)
• Some of these cases will be studied more later in the semester

Similarity Dimension

• Easy to calculate dimension for exactly self-similar fractals
• Example #1  (Sierpinski carpet):
• 
• Consists of 9 squares in a 3 x 3 array
• Eight squares are self-similar squares and one is empty
• Each time the linear scale is increased 3 x, the "stuff" increases 8 times

Hence, D = log(8) / log(3) = 1.892789261...
• Note: Any base can be used for log since it involves a ratio
• Example #2  (Koch curve):
• 
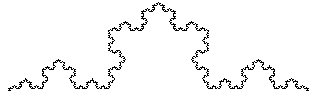
• Consists of 4 line segments:  _/\_
• Each factor of 3 increase in length adds 4 x the "stuff"

Hence, D = log(4) / log(3) = 1.261859507...
• Example #3  (Triadic Cantor set):
• 
• Consists of three line segments  ^{_____ _____ _____}
• Two segments are self similar and one is empty
• Each factor of 3 increase in length adds 2 x the "stuff"
• Hence, D = log(2) / log(3) = 0.630929753