According to the Poincare-Bendixson theorem, chaos cannot occur in 2-dimensional systems of autonomous ordinary differential equations (ODEs) such as
dx/dt = f(x, y)
dy/dt = g(x, y)
However, when such equations are solved numerically, the continuous flows represented by the ODEs are approximated by discrete-time maps. One conceptually simple method for implementing such a solution is the Euler method,
xn+1 = xn + hf(xn,
yn)
yn+1 = yn + hg(xn,
yn)
where h is a small time step. If h is sufficiently small, the solution of the map approximates the solution of the flow with arbitrary accuracy provided cumulative round-off error is kept small by calculating with adequate floating point number precision. However, if h is too large, the numerical solution will deviate significantly from the real solution and will eventually approach a periodic cycle, strange attractor, or will escape to infinity, often with all three behaviors appearing in sequence as h is increased.
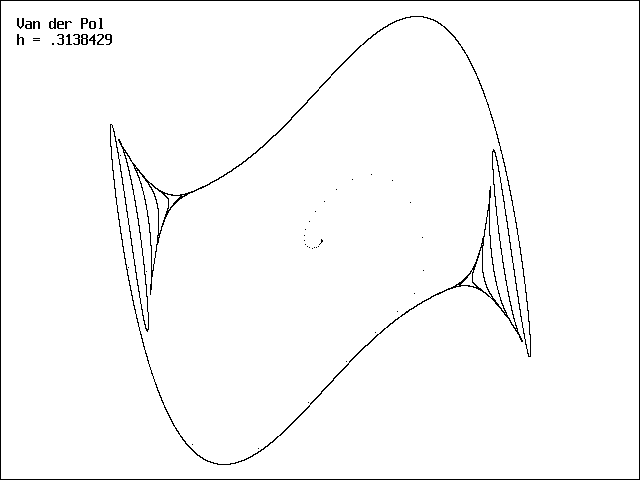
As an example, consider the Van der Pol oscillator, given by
dx/dt = y
dy/dt = b(1 - x2)y -
x
whose solution is a limit cycle. It has been used to model electrical oscillators, heartbeats, and pulsating stars called Cephids. This equation with b = 1 is solved by the Euler method in the DOS-executable program EULERMAP.EXE whose BASIC source code is available as EULERMAP.BAS. For h less than about 0.1 the solution is reasonably accurate, but for larger h, the typical periodic cycle to chaos to unbounded solution is observed. An example of the solution in the chaotic regime for an initial condition of x0 = y0 = 0.01 is shown below:

A similar system with a circular limit-cycle (x2 + y2 = 1) attractor is given by the equations
dx/dt = y
dy/dt = (1 - x2 - y2)y
- x
It's behavior is similar to the Van der Pol equation and with a sufficiently large h produces the strange attractor below:

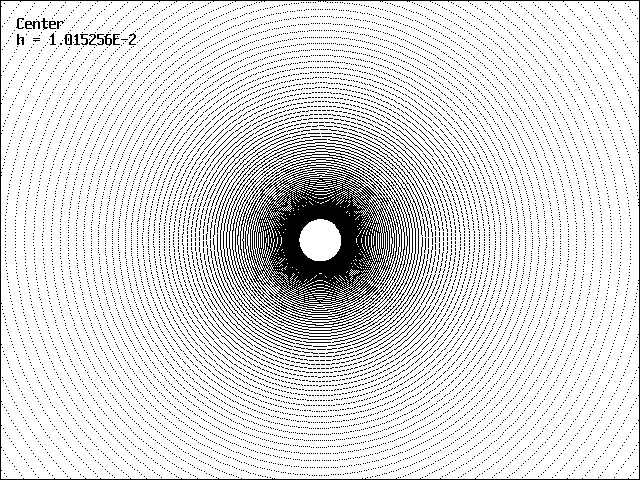
In the absence of dissipation, a Hamiltonian system characteristic of a simple harmonic oscillator is obtained
dx/dt = y
dy/dt = -x
whose phase-space solution is a circular trajectory about a center at x = y = 0. The trajectory should exactly close on itself after one period, independent of the initial condition. When solved with the Euler method, the trajectory does not close on itself for any h but spirals outward. This is because each iteration advances the trajectory along a tangent to the circle at the position of the previous iterate. A typical trajectory is shown below:
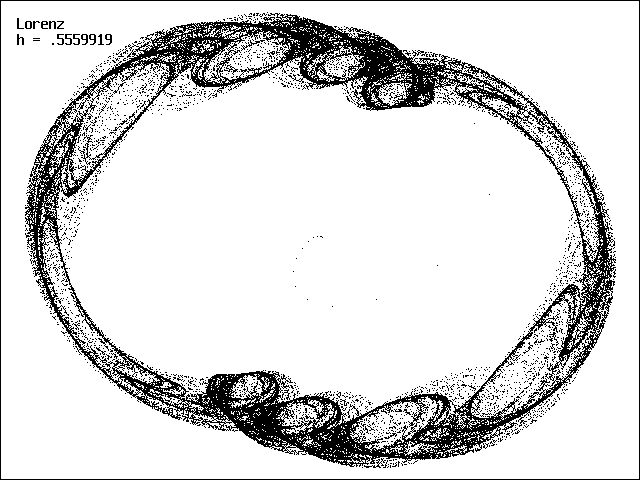
A final example is given by the system suggested by E. N. Lorenz in The Essence of Chaos,
dx/dt = x - y - x3
dy/dt = x - x2y
which also has an approximately circular limit cycle. With a sufficiently large h, this system when solved by the Euler method also gives a strange attractor as shown below:
Although these examples suggest that the Euler method is seriously flawed, most other numerical methods also exhibit the same phenomena if a sufficiently large step size is taken.
Ref: J. C. Sprott, Chaos and Time-Series Analysis (Oxford University Press, 2003), pp.63-65.