Dynamical Models of Love
J. C. Sprott
Department of Physics, University
of
Wisconsin - Madison
ABSTRACT
Following a suggestion of Strogatz, this paper examines a sequence
of dynamical models involving coupled ordinary differential
equations describing the time-variation of the love or hate
displayed by individuals in a romantic relationship. The models
start with a linear system of two individuals and advance to love
triangles and finally to include the effect of nonlinearities, which
are shown to produce chaos.
Ref: J. C. Sprott, Nonlinear
Dynamics, Psychology, and Life Sciences 8, 303-313 (2004).
The complete paper is available in
PDF format.
See the companion paper on Dynamical
Models of Happiness.
A less technical, more personal version of this is in Chapter 18
of my
Memoirs.
Return to Sprott's Books and Publications.
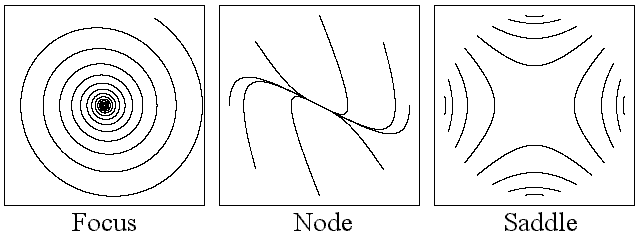
Fig 1. Dynamics in the vicinity of an equilibrium point in two
dimensions from Eq. 1.

Fig. 2. One solution of the linear love triangle in Eq. 3.

Fig. 3. One solution of the nonlinear Romeo-Juliet dynamic in
Eq. 4.
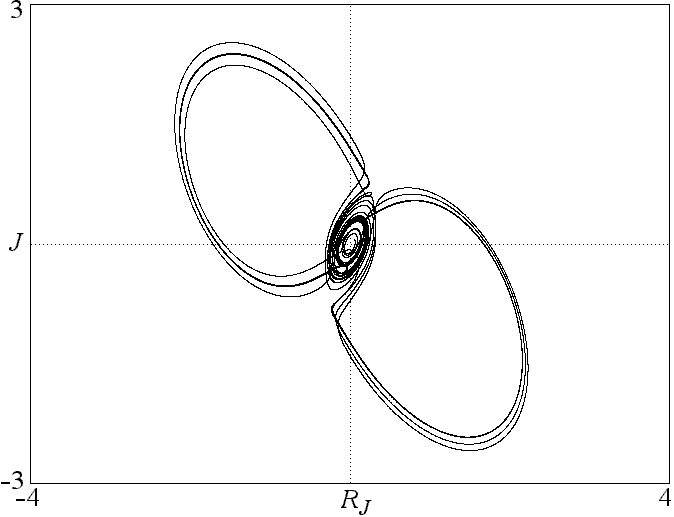
Fig. 4. Strange attractor from the nonlinear love triangle in
Eq. 5.
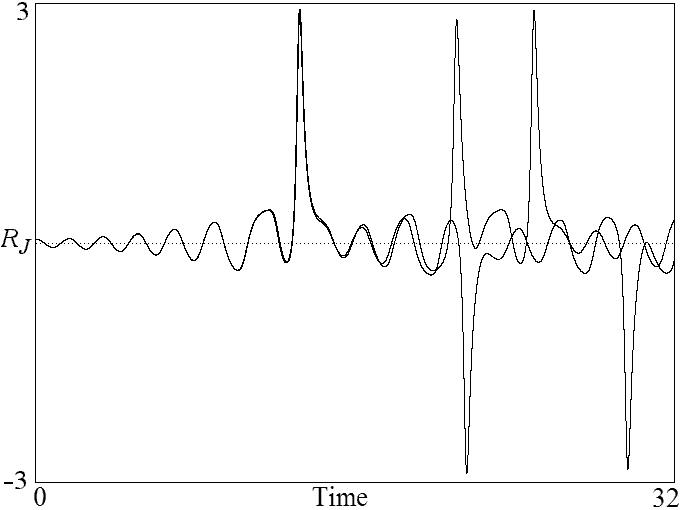
Fig. 5. Chaotic evolution of Romeo's love for Juliet from Eq. 5
showing the effect of changing the initial conditions by 1%.




