SIMPLEST 3D CONTINUOUS-TIME QUADRATIC SYSTEMS AS CANDIDATES FOR GENERATING MULTISCROLL CHAOTIC ATTRACTORS

ZERAOULIA ELHADJ
Department of Mathematics,
University of T´ebessa, 12002, Algeria
zeraoulia@mail.univ-tebessa.dz
zelhadj12@yahoo.fr

J. C. SPROTT
Department of Physics, University of Wisconsin,
Madison, WI 53706, USA
sprott@physics.wisc.edu

Received September 13, 2012; Revised March 19, 2013

ABSTRACT

In this paper, we present a simple approach to produce n-scroll chaotic attractors in 3D quadratic continuous time systems. The method of analysis is based on the number of equilibrium points. Some numerical results are also given and discussed.

Ref: E. Zeraoulia and J. C. Sprott, International Journal of Bifurcation and Chaos 23, 1350120 (2013)

The complete paper is available in PDF format.

Return to Sprott's Books and Publications.


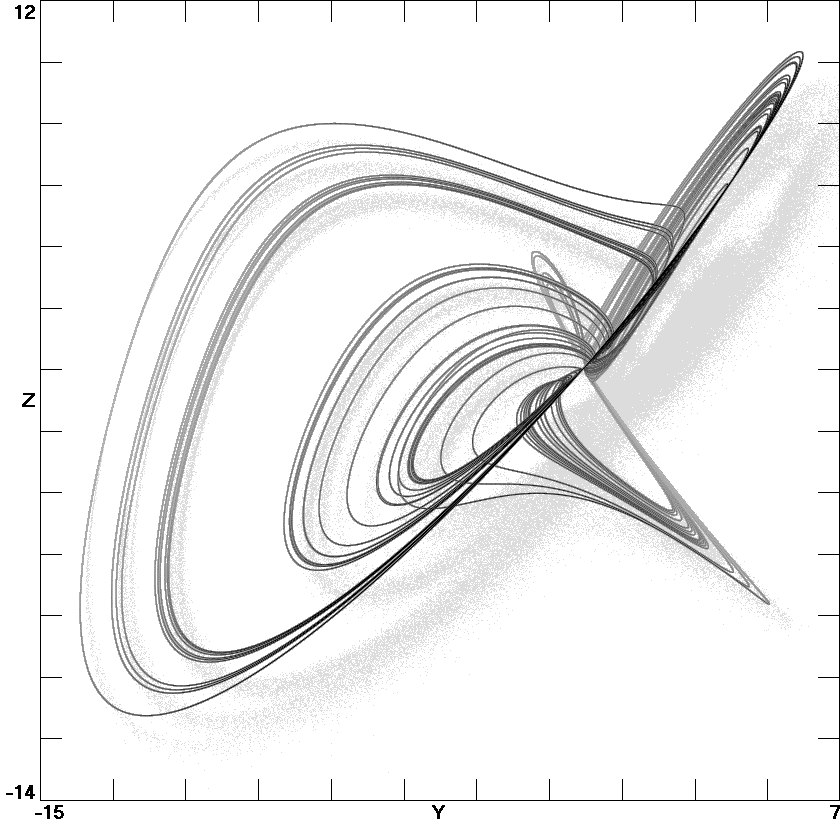
Figure 1
Fig. 1. A three-scroll attractor of system (16) with c8 = 0.23.

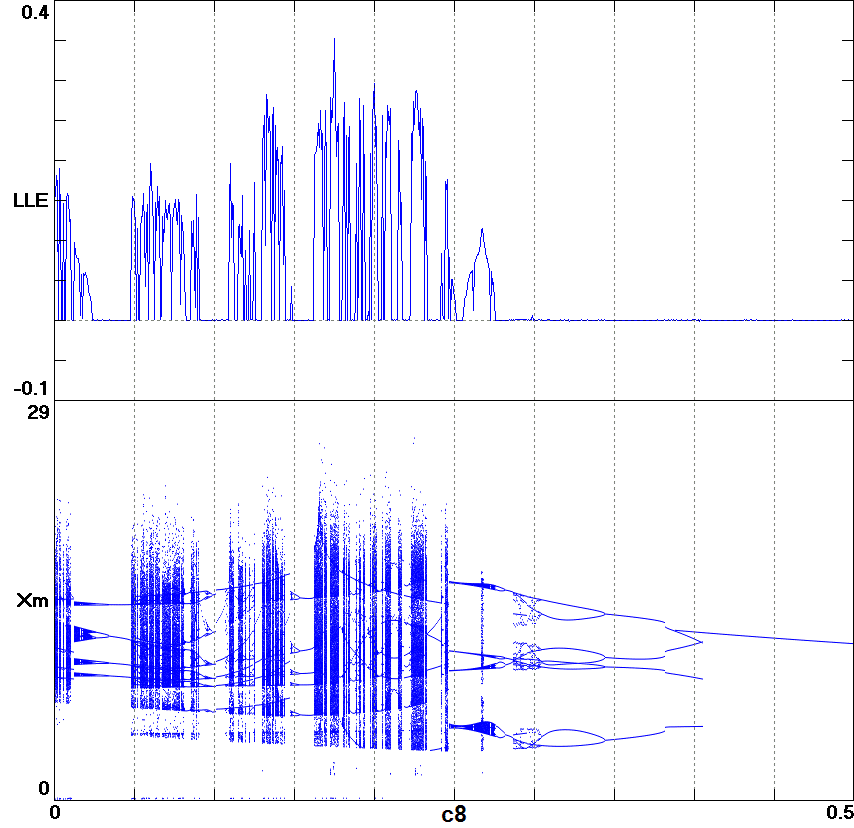
Figure 2
Fig. 2. Bifurcation diagram of system (16) for c8 < 0.5

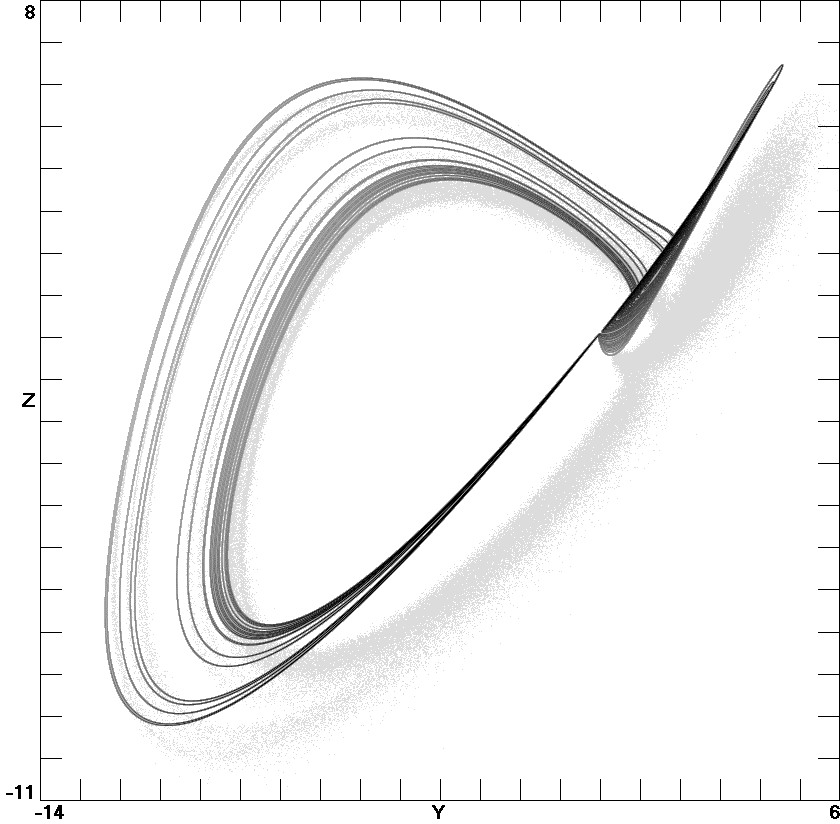
Figure 3
Fig. 3. A three-scroll chaotic attractor of system (16) with c8 = 0.0.

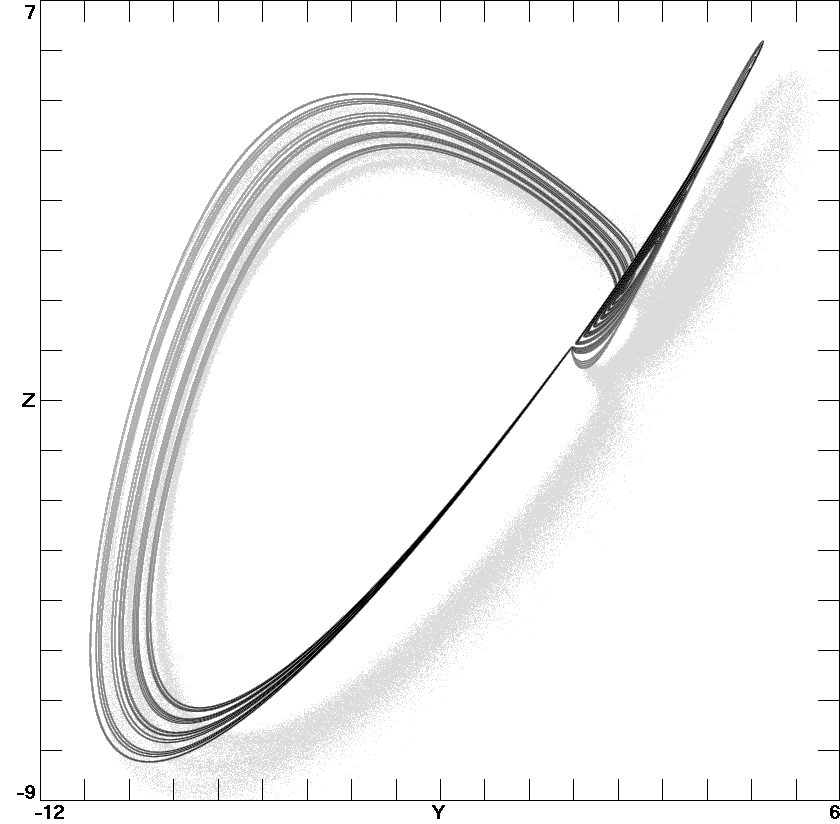
Figure 4
Fig 4. A three-scroll chaotic attractor of system (16) with c8 = 0.07.

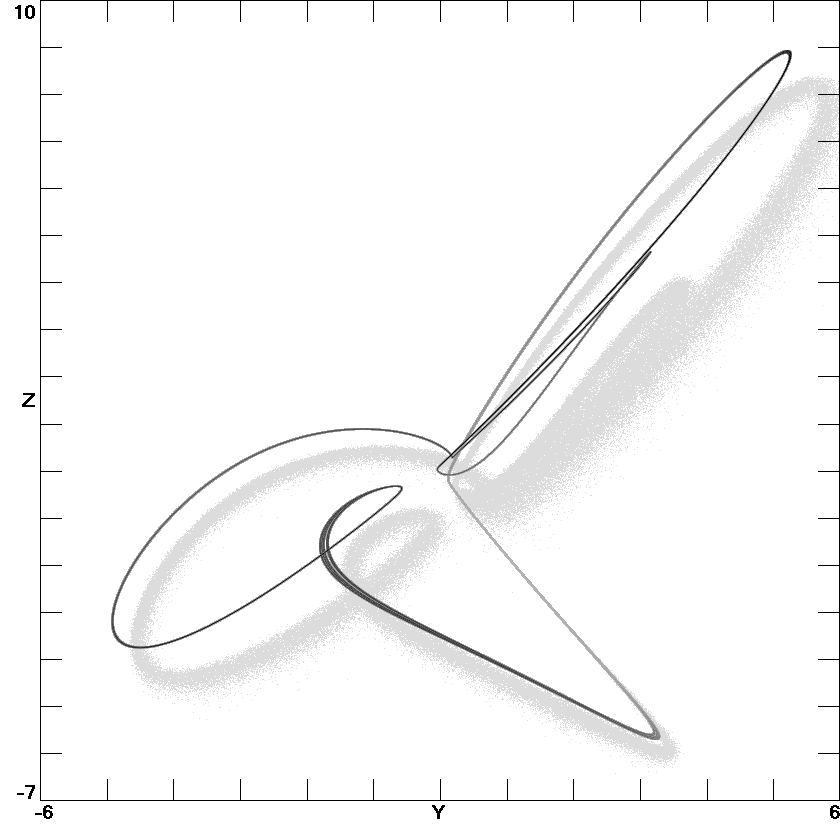
Figure 5
Fig. 5. A three-scroll attractor of system (16) with c8 = 0.25.

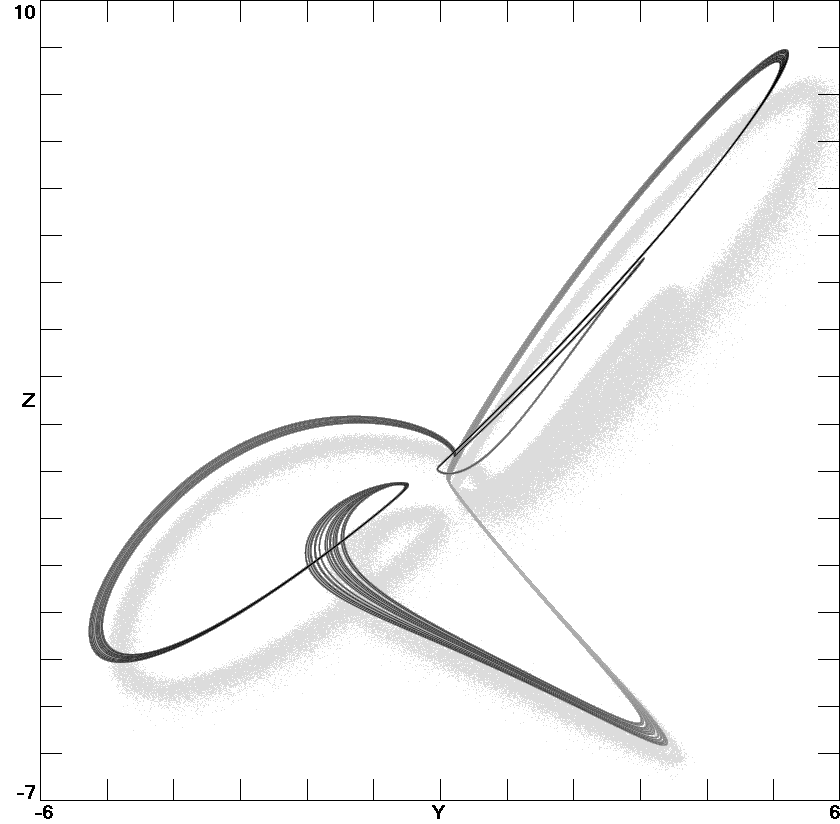
Figure 6
Fig. 6. A three-scroll chaotic attractor of system (16) with c8 = 0.27.