Other Fractal Sets

Comments on Homework #12 (Correlation Dimension)

• This was one of the harder assignments but most useful
• Most people got a reasonable value of D₂ = 1.21 ± 0.1
• A few people got D₂ < 1 (perhaps embedded in 1D ?)
• Your Hénon C(r) should look like this with 1000 data points
• The D₂ versus log r plot should approach this with many data points
• See also a detailed discussion of this problem

Review (last week) - Multifractals

• Tips for speeding up D₂ calculation
• Number of data points needed is N ~ 10 ^{2 + 0.4D}2  (Tsonis criterion)
• Round-off errors descretize the state space and narrow scaling region
• Superimposed noise makes dimension high at small r
• Colored noise may be impossible to distinguish from chaos (conjecture)
• Kolmogorov-Sinai (K-S) entropy
• Sum of the positive Lyapunov exponents (Pesin Identity)
• It is actually a rate of change of the usual entropy
• Estimate:  K = d log C(r)/dD_E in the limit of infinite D_E
• Multivariate data can be combined with intercalation
• Filtering data should be harmless but often isn't
• Missing data can be reconstructed but should not be ignored
• Nonuniform sampling is OK if nonuniformity it deterministic
• Lack of stationarity
• dx/dt = F(x, y)
• dy/dt = G(x, y, t)
• dz/dt = 1  (non-autonomous slowly growing term)
• Increases system dimension by 1
• Increases attractor dimension by < 1
• If t is periodic, attractor projects onto a torus
• Can try to detrend that data
• This is problematic
• How best to detrend? (polynomial fit, sine wave, etc.)
• What is interesting dynamics and what is uninteresting trend?
• Take log first differences: Y_n = log(X_n) - log(X_n-1) = log(X_n/X_n-1)
• Surrogate data
• Generate data with same power spectrum but no determinism
• This is colored noise
• Take Fourier transform, randomize phases, inverse Fourier transform
• Compare C(r), predictability, etc.
• Many surrogate data sets allow you to specify confidence level

Multifractals

• Most attractors are not uniformly dense
• Orbit visits some portions more often than others
• Local fractal dimension may vary over the attractor
• Capacity dimension (D₀) weights all portions equally
• Correlation dimension (D₂) emphasizes dense regions
• q = 0 and 2 are only two possible weightings
• Let C_q(r) = S [ S q(r - Dr) / (N - D)]^q-1 / (N - D + 1)
• Then D_q = [d log C_q(r)/d log r] / (q - 1)
• Note: for q = 2 this is just the correlation dimension
• q = 0 is the capacity dimension
• q = 1 is the information dimension
• Other values of q don't have names (so far as I know)
• q can be negative (or non-integer)
• There are (multiply) infinitely many dimensions
• q = infinity is dimension of densest part of attractor
• q = -infinity is dimension of sparsest part of attractor
• All dimensions are the same if the attractor is uniformly dense
• Otherwise, we call the object a multifractal
• In general, dD_q/dq < 0:


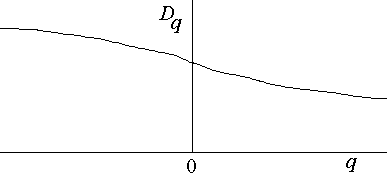
• The K-S entropy can also be generalized

K_q = -log S p_i^q / (q - 1)N

Summary of Time-Series Analysis

• Verify integrity of data
• Graph X(t)
• Correct bad or missing data
• Establish stationarity
• Observe trends in X(t)
• Compare first and second half of data set
• Detrend the data
• Take (log) first differences
• Fit to low-order polynomial
• Fit to superposition of sine waves
• Examine data plots
• X_i versus X_i-1
• Phase space plots (dX/dt versus X)
• Return maps (max X versus previous max X, etc.)
• Poincaré sections
• Determine correlation time or minimum of mutual information
• Look for periodicities (if correlation time decays slowly)
• Use FFT to get power spectrum
• Use Maximum entropy method (MEM) to get dominant frequencies
• Find optimal embedding
• False nearest neighbors
• Saturation in correlation dimension
• Determine correlation dimension
• Make sure log C(r) versus log r has scaling (linear) region
• Make sure result is insensitive to embedding
• Make sure you have sufficient data points (Tsonis)
• Determine largest Lyapunov exponent and entropy (if chaotic)
• Determine growth of unpredictability
• Try to remove noise if dimension is too high
• Integrate data
• Use nonlinear predictor
• Use principal component analysis (PCA)
• Construct model equations
• Make short-term predictions
• Compare with surrogate data sets

Time-Series Analysis Tutorial (using CDA)

• Sine wave
• Two incommensurate sine waves
• Logistic map
• Hénon map
• Lorenz attractor
• White noise
• Mean daily temperatures
• Standard & Poor's Index of 500 common stocks

Iterated Function Systems

• 2-D Linear affine transformation
• X_n+1 = aX_n + bY_n + e
• Y_n+1 = cX_n + dY_n + f
• Area expansion:  A_n+1/A_n = det J = ad - bc
• Contraction:  |ad - bc| < 1
• Translation:  e, f < > 0
• Rotation:  a = d = r cos q, b = -c = -r sin q
• Shear:  bd < > -ac
• Reflection:  ad - bc < 0
• Such transformations can be extended to 3-D and higher
• To make an IFS fractal:
• Specify two or more affine transformations
• Choose a random sequence of the transformations
• Apply the transformations in sequence
• Repeat many times
• Helps to weight the probabilities proportional to |det J|
• Examples of IFS fractals produced this way
• These were produced with two 2-D transformations
• Can also use two 3-D transformations and color the third D
• Aesthetic preferences are for high LE and high D₂
• Note that LE is actually negative (all directions contract)
• Can also colorize by the number of successive applications of each transform
• IFS compression
• With enough transformations, any image can be replicated
• Method pioneered by Barnsley & Hurd
• Barnsley started company, Iterated Systems, to commercialize this
• Used to produce images in Microsoft Encarta (CD-ROM encyclopedia)
• Uses the collage theorem to find optimal transformations
• Compression is lossy and slow (proprietary)
• 10 - 100 x compressions are typical
• Decompression is fast
• Provides unlimited resolution (but fake)
• IFS clumpiness test
• Use time-series data instead of random numbers
• Play the chaos game, for example with a square
• Divide the range of data into 4 quartiles
• Random data (white noise) fills the square uniformly


• Chaotic data (i.e., logistic map) produces a pattern


• The eye is very sensitive to patterns of this sort
• This has been done with the sequence of 4 bases in DNA molecule
• It can also be done with speech or music
• Caution - colored noise (i.e., 1/f) also makes patterns

Mandelbrot and Julia Sets

• Non-Attracting Chaotic Sets
• These sets ARE attracting
• They are generally only transiently chaotic
• Derivation from logistic equation
• Start with logistic equation:  X_n+1 = AX_n(1 - X_n)
• Define a new variable:  Z = A(1/2 - X)
• Solve for X(Z, A) to get:  X = 1/2 - Z/A
• Substitute into logistic equation:  Z_n+1 = Z_n² + c
• Where  c = A/2 - A²/4
• Range (1 < A < 4)  ==>  -2 < c < 1/2
• Z_n+1 = Z_n² + c is equivalent to logistic map
• General the above to complex values of Z and c
• Review of complex numbers
• Z = X + iY, where i = (-1)^1/2
• Z² = X² + 2iXY - Y²
• Separate real and imaginary parts
• X_n+1 = X_n² - Y_n² + a
• Y_n+1 = 2X_nY_n + b
• where a = Re(c) and b = Im(c)
• This is just another 2-D quadratic map
• X, Y, a, and b are real variables
• Orbits are either bounded or unbounded
• Mandelbrot (M) set
• Region of a-b space with bounded orbits with X₀ = Y₀ = 0
• Orbit escapes to infinity if X² + Y² > 4 (circle of radius 2)
• It's sometimes defined as the complement of this
• There is only one Mandelbrot set
• The "buds" in the M-set correspond to different periodicities
• Usually plotted are escape-time contours in colors
• Each point in the M-set has a corresponding Julia set
• The M-set is everywhere connected
• Boundary of M-set is fractal with dimension = 2 (proved)
• Area of set is ~ p/2
• Points along the real axis replicate logistic map and exhibit chaos
• Points just outside the boundary exhibit transient chaos
• The chaotic region appears to be a set of measure zero (not proved)
• Boundary of M-set is a repellor
• With deep zoom, M-set and J-set are identical
• People have zoomed in by factors as large as 10¹⁶⁰⁰
• Miniature M-sets are found at deep zooms
• See the Mandelbrot Java applet written by Andrew R. Cavender
• Julia (J) sets
• Region of X₀-Y₀ space with bounded orbits for given a, b
• Orbit escapes to infinity if X² + Y² > 4 (circle of radius 2)
• This is sometimes called the "filled-in" Julia set
• There are infinitely many J-sets
• Usually plotted are escape-time contours in colors
• The J-sets correspond to points on the Mandelbrot set
• J-sets from inside the M-set are connected
• J-sets from outside the M-set are "dusts"
• Boundary of J-set is a repellor
• With deep zoom, J-set and M-set are identical
• Fixed points of Julia sets
• Z = Z² + c  ==>  Z = 1/2 ± (1 - 4c)^1/2/2
• These fixed points are unstable (repellors)
• They can be found by backward iteration:  Z_n = ± (Z_n+1 - c)^1/2
• There are two roots (pre-images) each with two roots, etc.
• Find them with the random iteration algorithm (cf: IFS)
• The repelling boundary of J-set thus becomes an attractor
• An example is the Julia dendrite  (c = i)
• Generalized Julia sets
• Other complex functions Z_n+1 = F(Z_n) have interesting boundaries
• No good answer to what's special about these functions
• General 2-D quadratic map sometimes have interesting basin boundaries
• Fractal eXtreme has a plug-in for calculating these
• Applications of M-set and J-sets
• None known except computer art
• High traction shoe tread?

J. C. Sprott | Physics 505 Home Page | Previous Lecture | Next Lecture