Simple Chaotic Flows with a Line Equilibrium

Sajad Jafari
Biomedical Engineering Department, Amikabir University of Technology, Tehran 15875-4413, Iran

J. C. Sprott
Department of Physics, University of Wisconsin, Madison, WI 53706, USA

Received 12 June 2013, Accepted 20 August 2013

ABSTRACT

Using a systematic computer search, nine simple chaotic flows with quadratic nonlinearities were found that have the unusual feature of having a line equilibrium. Such systems belong to a newly introduced category of chaotic systems with hidden attractors that are important and potentially problematic in engineering applications.

Ref: S. Jafari and J. C. Sprott, Chaos Solitons & Fractals 57, 79-84 (2013)

The complete paper is available in PDF format. (See also the Erratum)

Return to Sprott's Books and Publications.

Figure 1
Fig. 1. State space plots of the cases in Table 1 projected on the xy-plane.

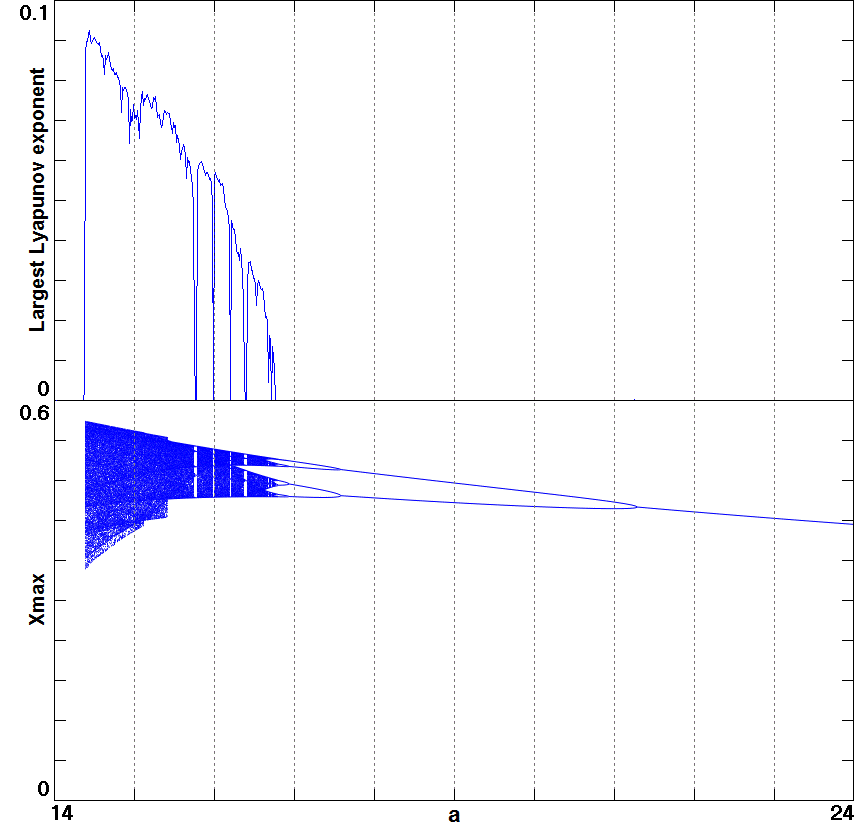
Figure 2
Fig. 2. The largest Lyapunov exponent and bifurcation diagram of case LE1 showing a period-doubling route to chaos.

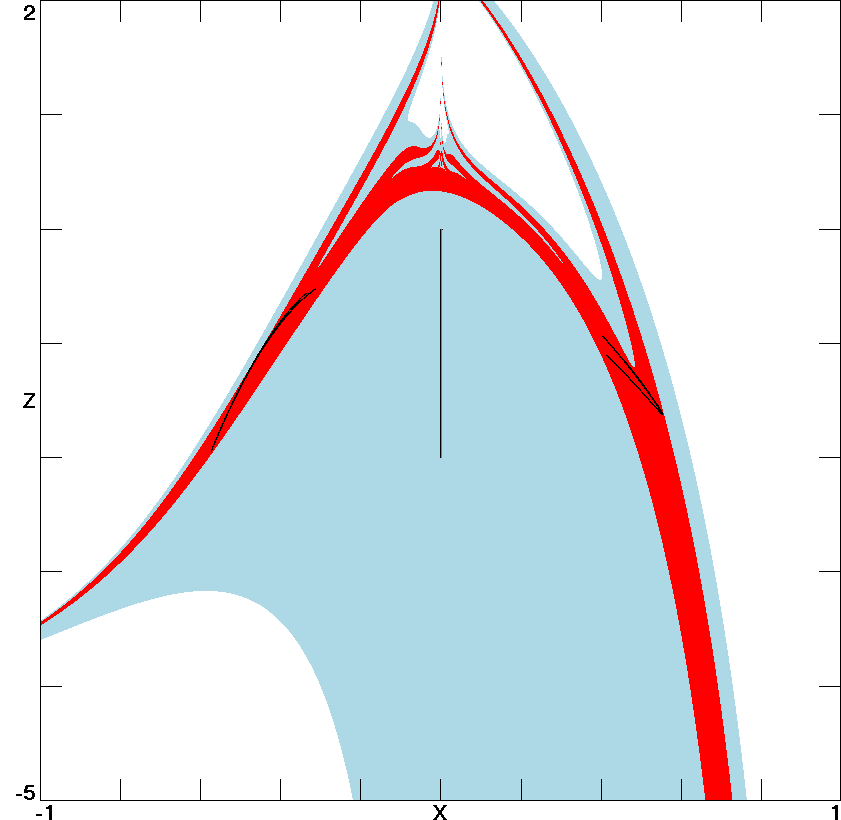
Figure 3
Fig. 3. Cross section of the basins of attraction of the two attractors in the xz-plane at y = 0 for case LE1. Initial conditions in the white region lead to unbounded orbits, those in the red region lead to the strange attractor, and those in the light blue region lead to the line equilibrium.

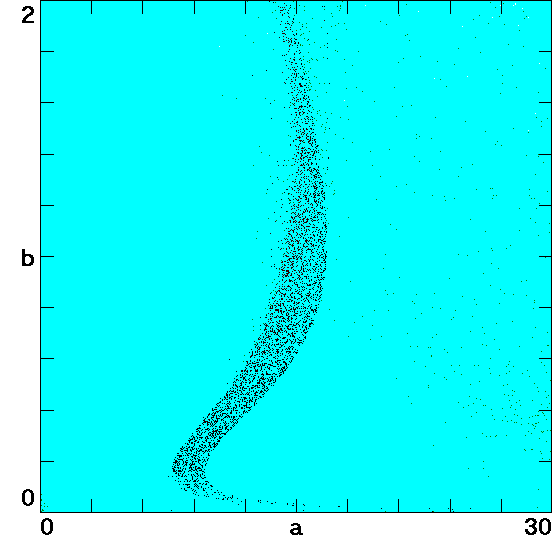
Figure 4
Fig. 4. Regions of different dynamic behavior in parameter space for case LE1. Light blue represents a static equilibrium, and the black dots correspond to regions of chaos. Each pixel uses a different random initial condition thereby indicating the coexistence of static and chaotic attractors.