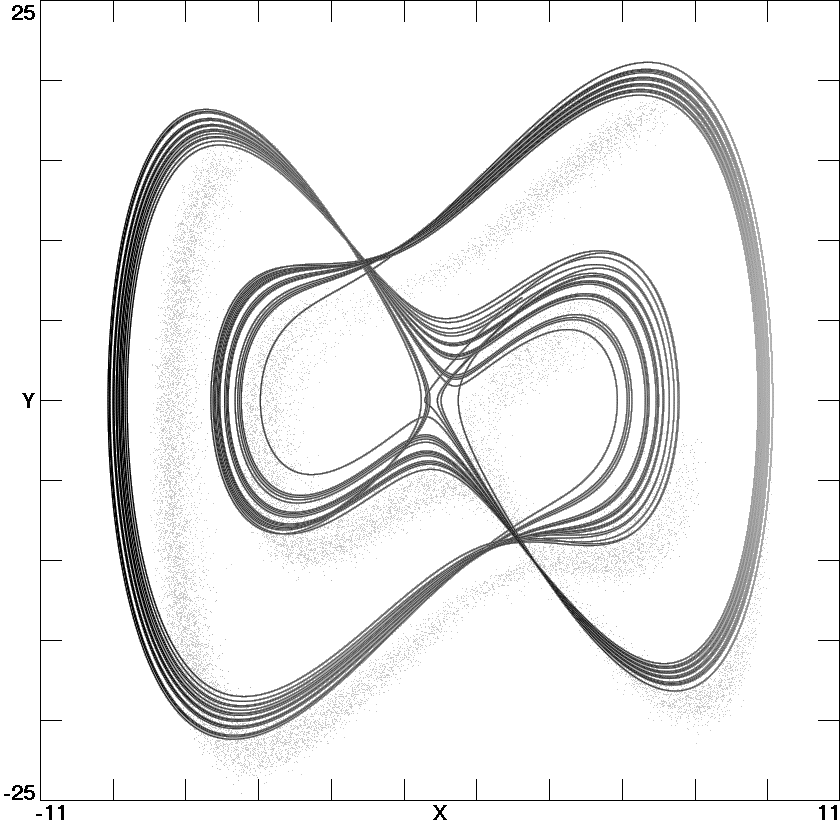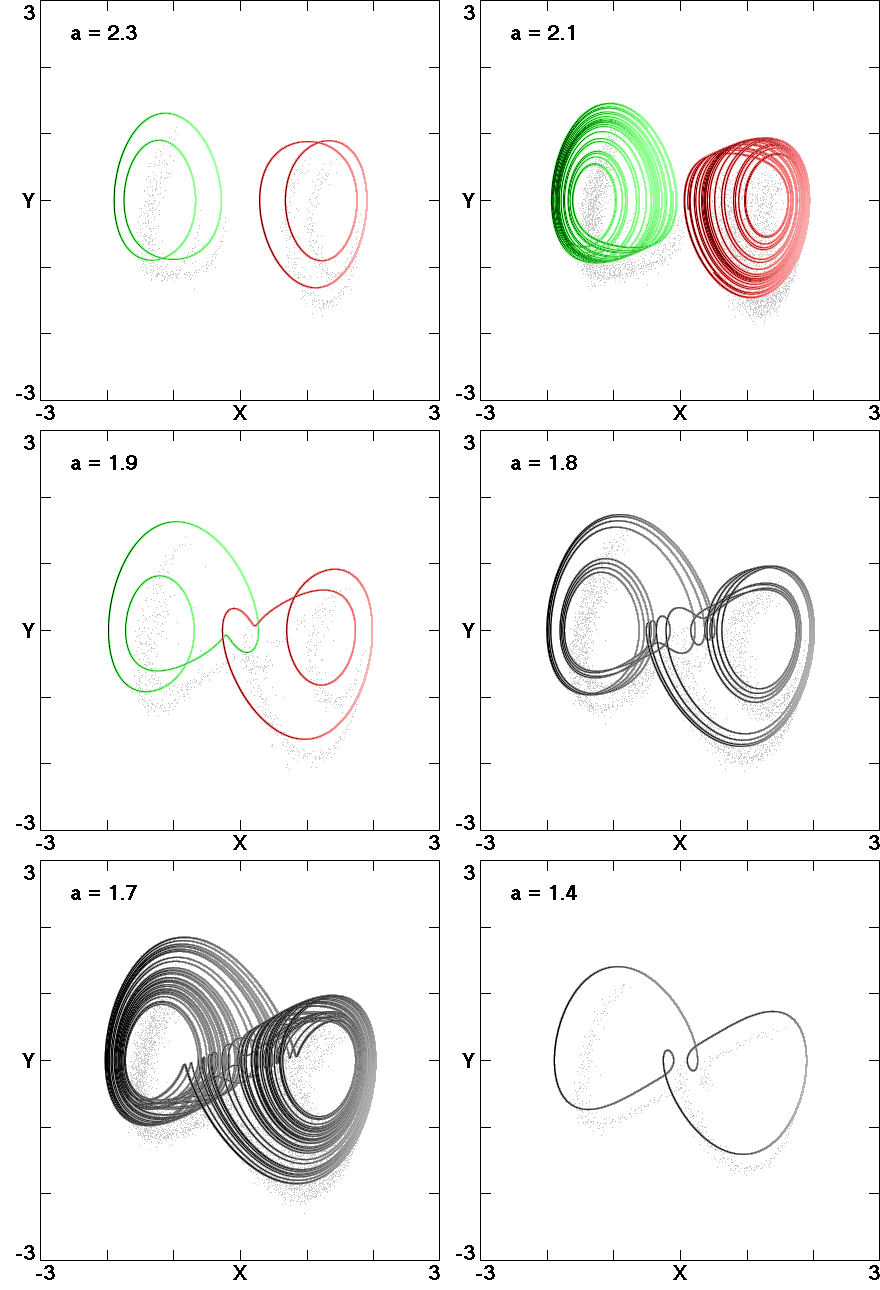Simplest Chaotic Flows with Involutional Symmetries

J. C. Sprott
Department of Physics, University of Wisconsin-Madison,
 Madison, WI 53706, USA
sprott@physics.wisc.edu

Received August 9, 2013

ABSTRACT
A chaotic flow has an involutional symmetry if the form of the dynamical equations remains unchanged when one or more of the variables changes sign. Such systems are of theoretical and practical importance because they can exhibit symmetry breaking in which a symmetric pair of attractors coexist and merge into one symmetric attractor through an attractor-merging bifurcation. This paper describes the simplest chaotic examples of such systems in three dimensions, including several cases not previously known, and illustrates the attractor-merging process.

Ref: J. C. Sprott, International Journal of Bifurcation and Chaos 24, 1450009 (2014)

The complete paper is available in PDF format.

Return to Sprott's Books and Publications.

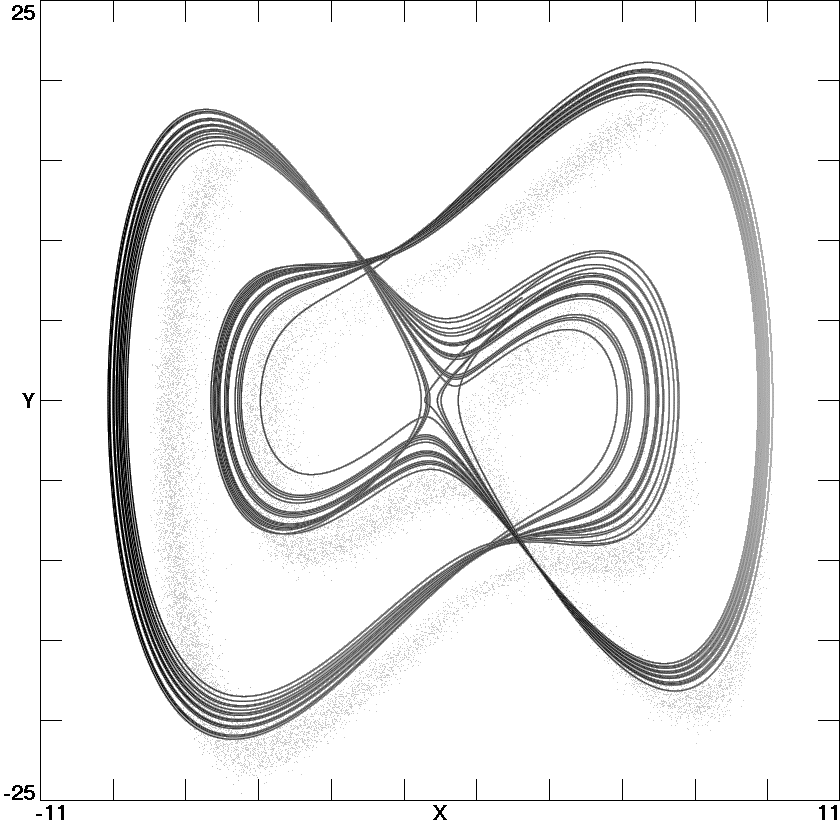
Figure 1
Fig. 1. Moore-Spiegel attractor from Eq. (1) with a = 9 and b = 5.

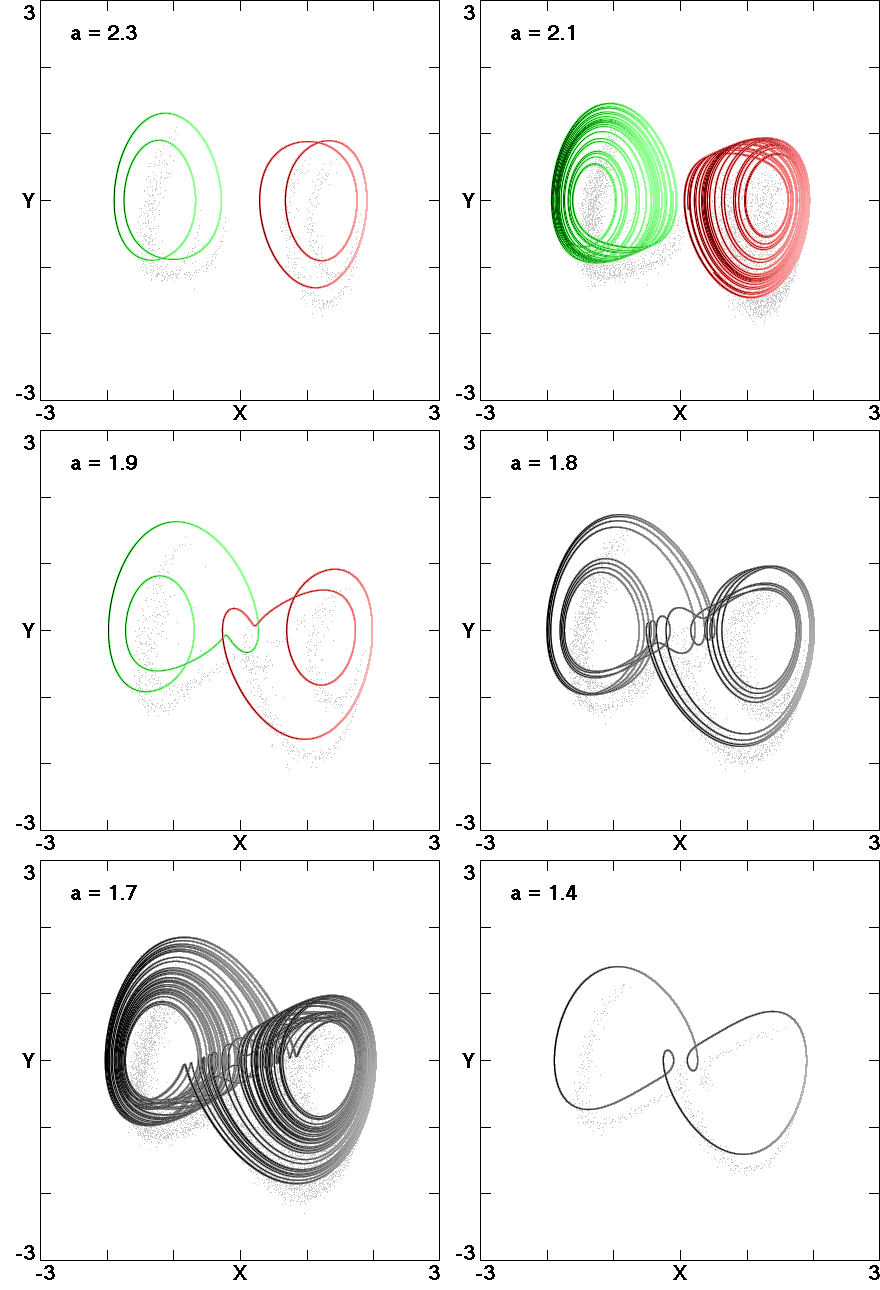
Figure 2
Fig. 2. Attractor merging from Eq. (2) with b = 2.

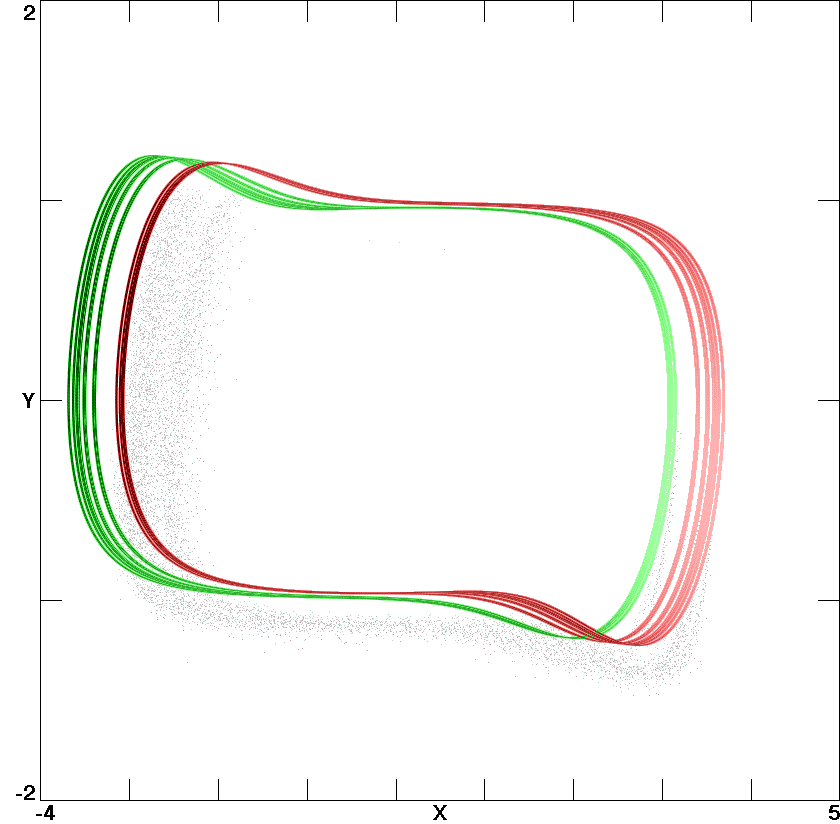
Figure 3
Fig. 3. Coexisting Malasoma strange attractors with a = 2.08.

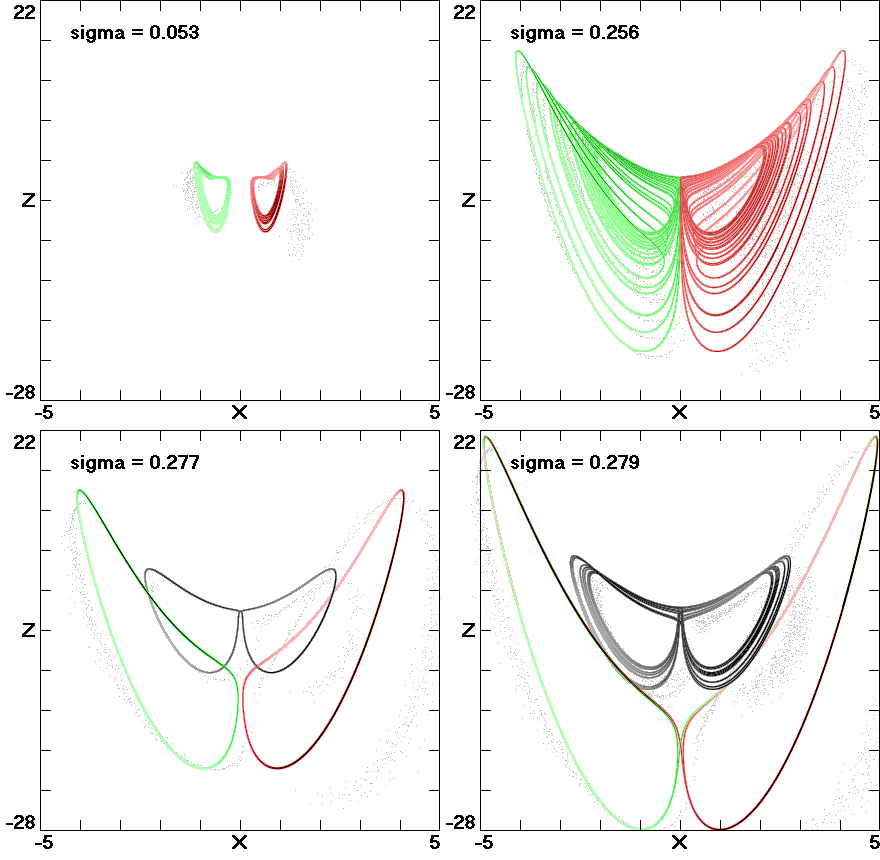
Figure 4
Fig. 4. Coexisting strange attractors in the Lorenz system with r = 0 and b = -0.3.

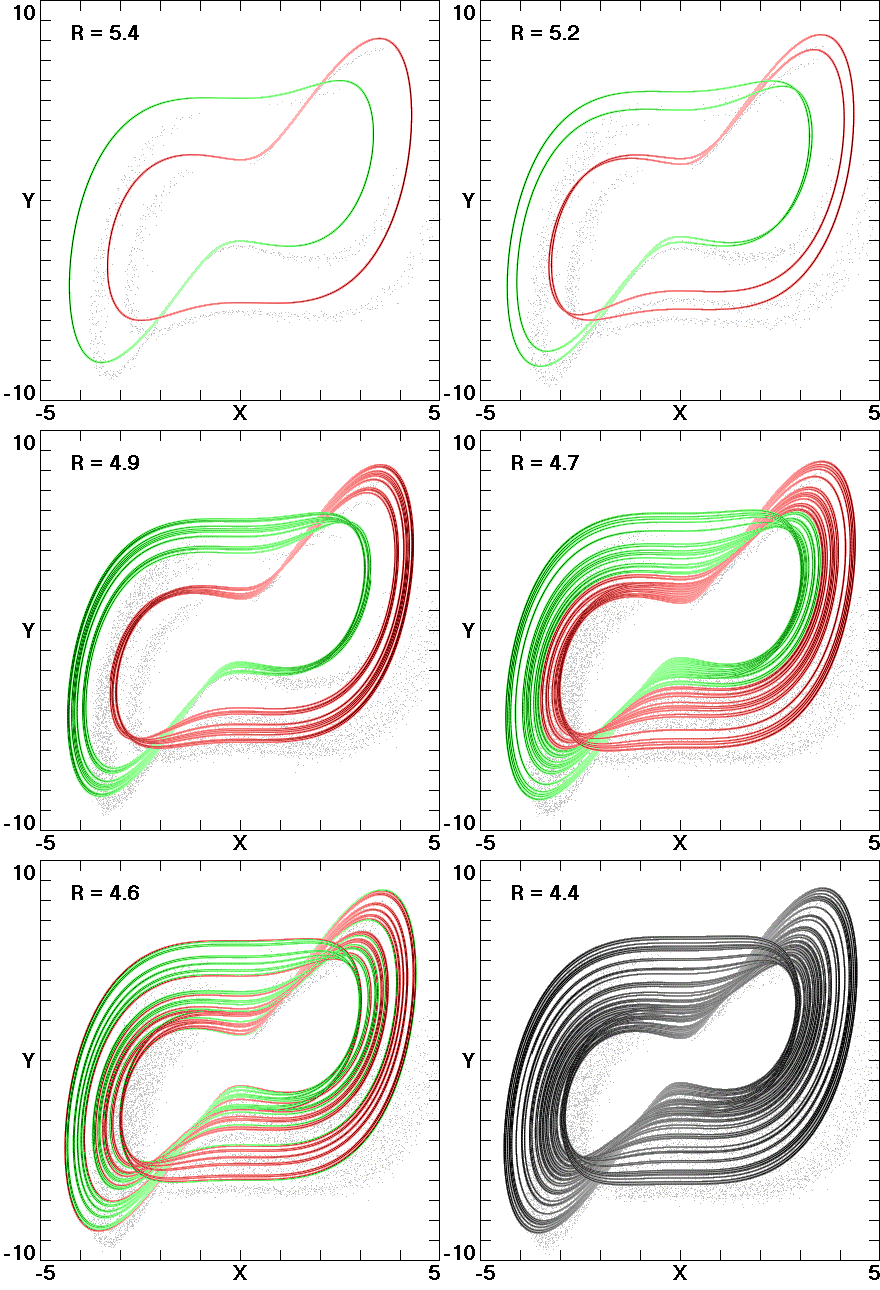
Figure 5
Fig. 5. Attractor merging for Eq. (5).

Figure 6
Fig. 6. Cross-section of the fractal basins of attraction in the z = 0 plane for Eq. (5) with R = 4.7. The black lines are cross-sections of the corresponding strange attractors that nearly touch their basin boundaries.

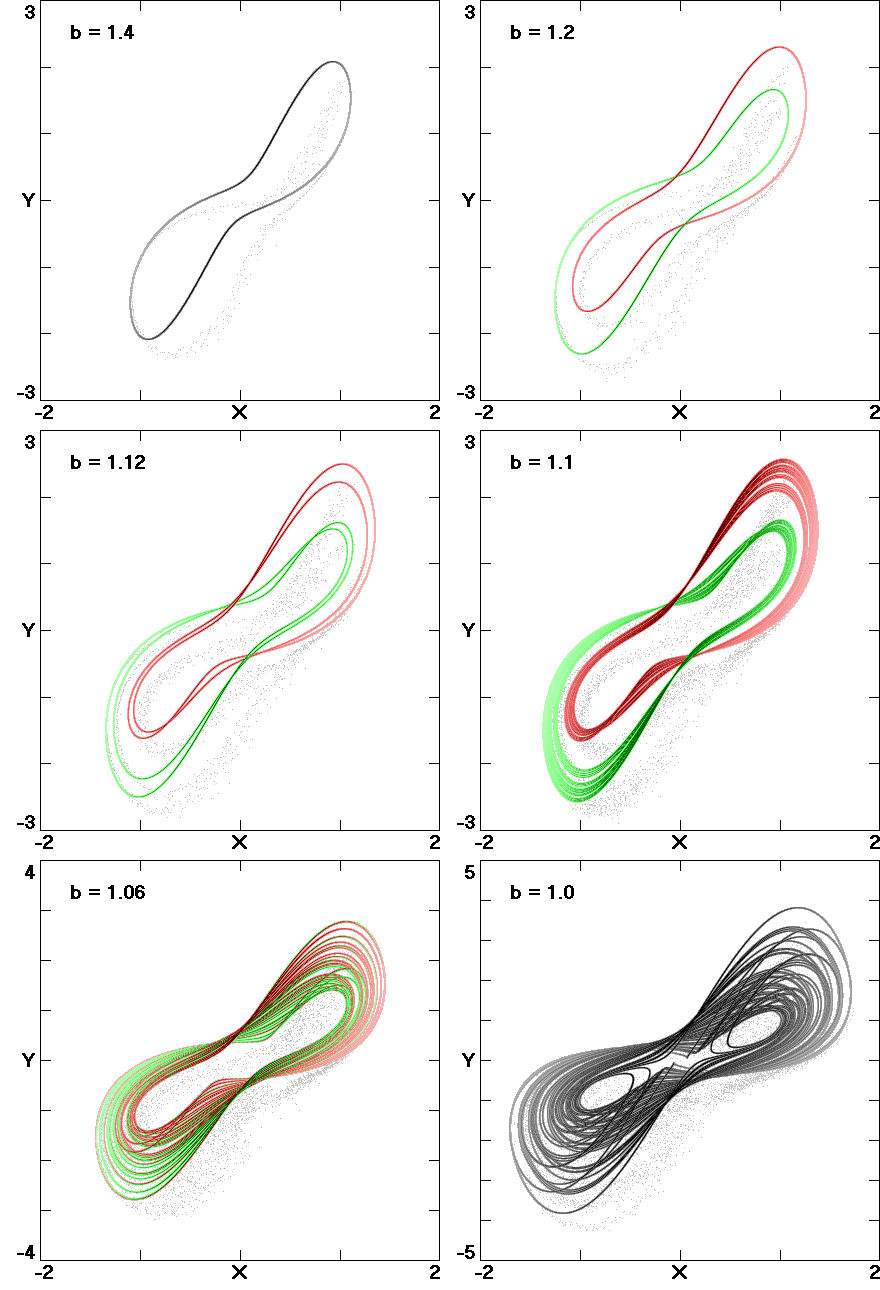
Figure 7
Fig. 7. Attractor merging for Eq. (6) with a = 1.

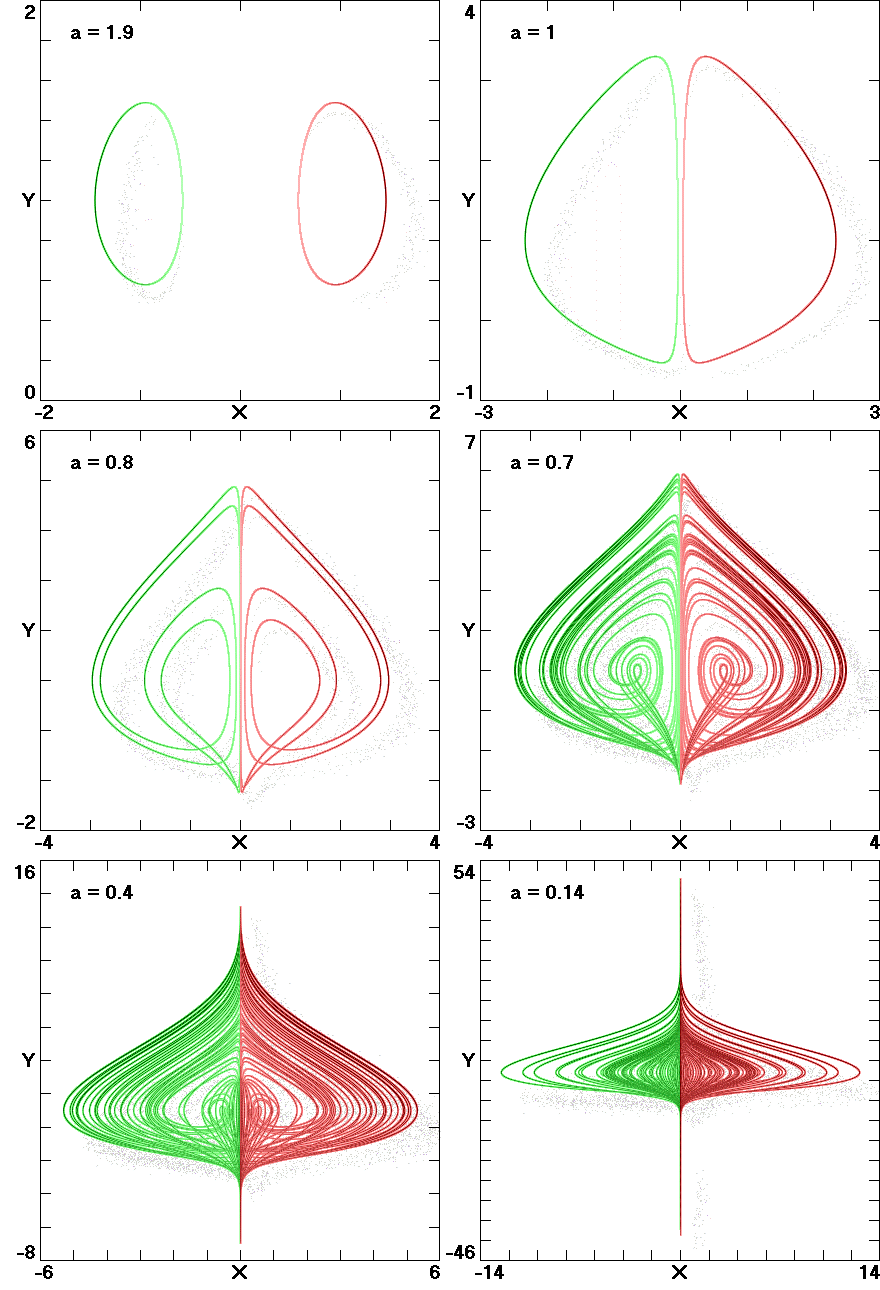
Figure 8
Fig. 8. Attractor "kissing" for Eq. (8).