Simple Conservative, Autonomous, Second-Order Chaotic Complex
Variable Systems
Delmar Marshall
Physics Department, Amrita
Vishwa Vidyepeetham, Clappana P.O., Kollam, Kerala 690-525,
India
J. C. Sprott
Physics Department, University
of Wisconsin, 1150 University Avenue, Madison, WI 53706,
USA
(Received April 22, 2008; Revised July 21, 2009)
ABSTRACT
It is shown that, for analytic functiions f, systems of the form z'' = f(z, z') and z''
= f(z) cannot produce chaos, and
that systems of the form z''
= f(z, z*) are conservative. Eight simple chaotic systems
of the form z'' = f(z, z*)
with quadratic and cubic polynomial f(z, z*) are given. Lyapunov spectra
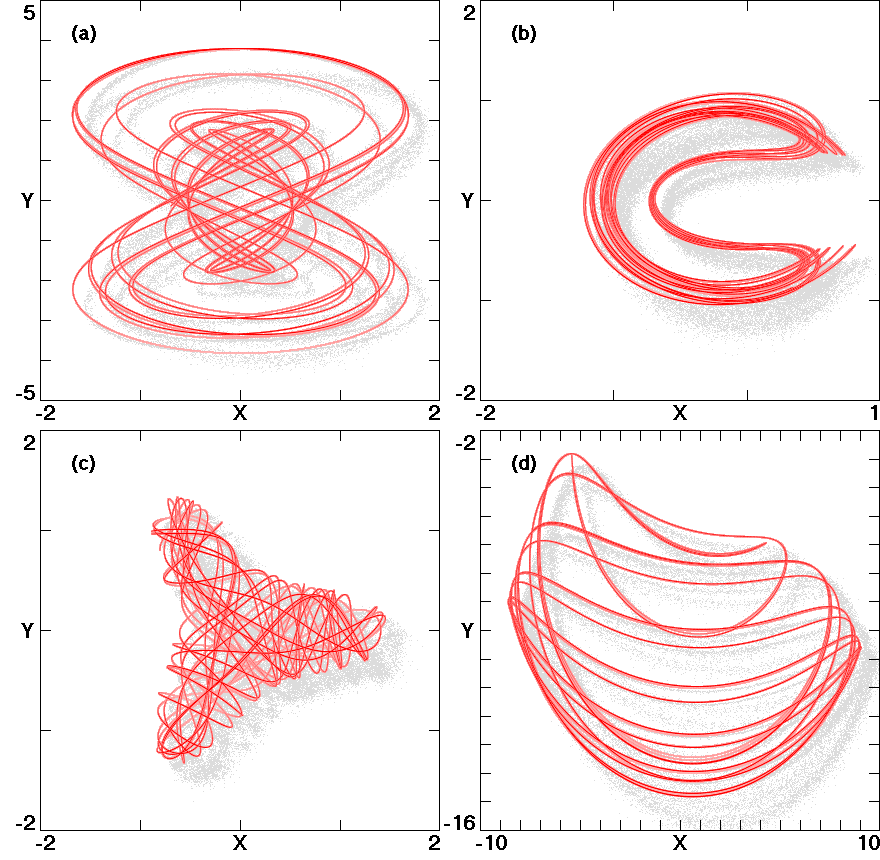
are calculated, and the systems' phase space trajectories are
displayed. For each system, a Hamiltonian is given, if one exists.
Ref: D. Marshall and J. C. Sprott,
Chaos 20, 697-702
(2010)
The complete paper is available
in PDF format.
Return to Sprott's Books and Publications.
Fig. 1.
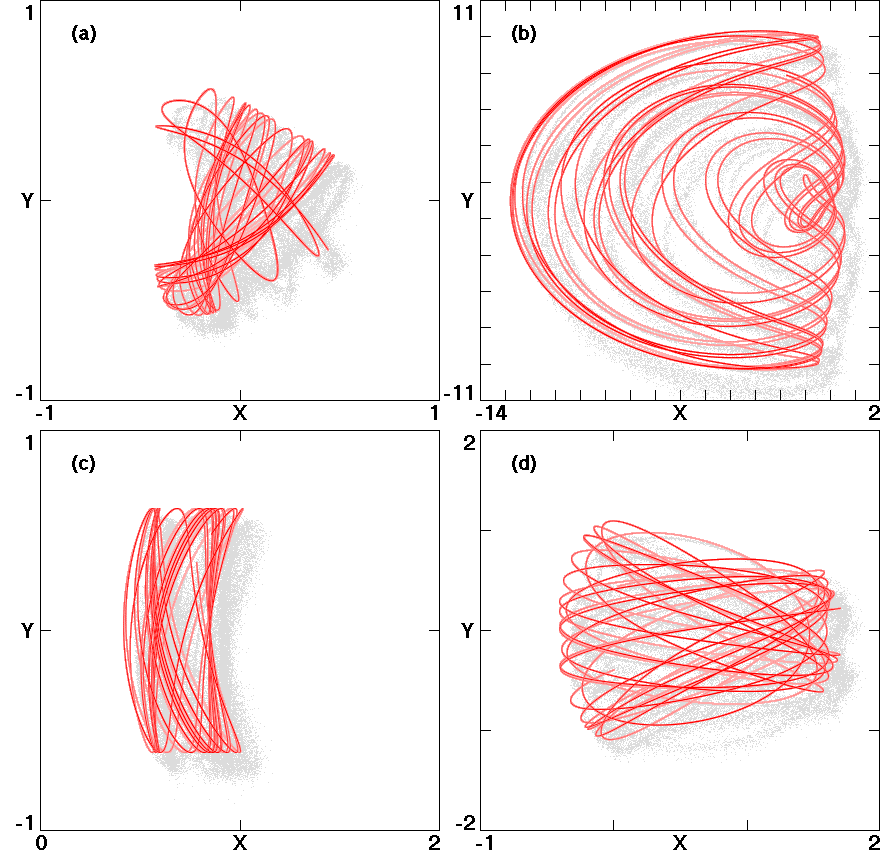
Fig. 2.