A Simple Diffusion Model Showing
Anomalous Scaling
G. Rowlands1 and J. C.
Sprott2
1Department of
Physics,
University of Warwick, Coventry CV4 7AL, England
2Department of
Physics,
University of Wisconsin, Madison, Wisconsin 53706, USA
�Received 25 April 2008; accepted 21 July 2008; published
online
13 August 2008
ABSTRACT
A number of iterated maps and one flow, which show chaotic behavior,
have been studied numerically and their time evolution expressed in
terms of higher-order moments Mm(t) All the cases show anomalous
behavior with Mm(t)
~ tg(m) with g(m) <> am.
A simple analytic
treatment isgiven based on an effective diffusion that is dependent
on
both space and time. This leads to a form for g(m)/m = a − b/m,
which is in good agreement with numerical results. This behavior is
attributed to the presence of convective motion superimposed on the
background diffusion, and hence this behavior is expected in a wide
variety of maps and flows.
Ref: G.
Rowlands and J. C. Sprott,
Physics of Plasmas 15,
082308-1 - 082308-7
(2008)
The complete paper is available
in PDF format.
Return to Sprott's Books and Publications.
Fig. 1. Intermittency in the Chirikov map for
K = 2.2
pi.
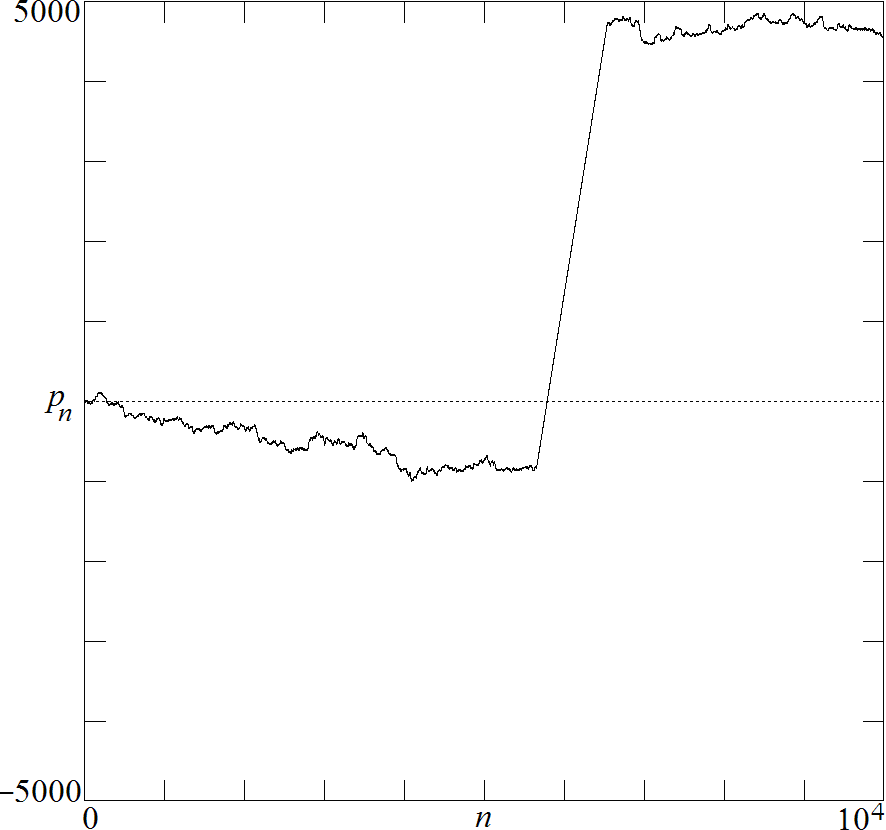
Fig. 2. Anomalous scaling in the Chirikov map as a function of
K.
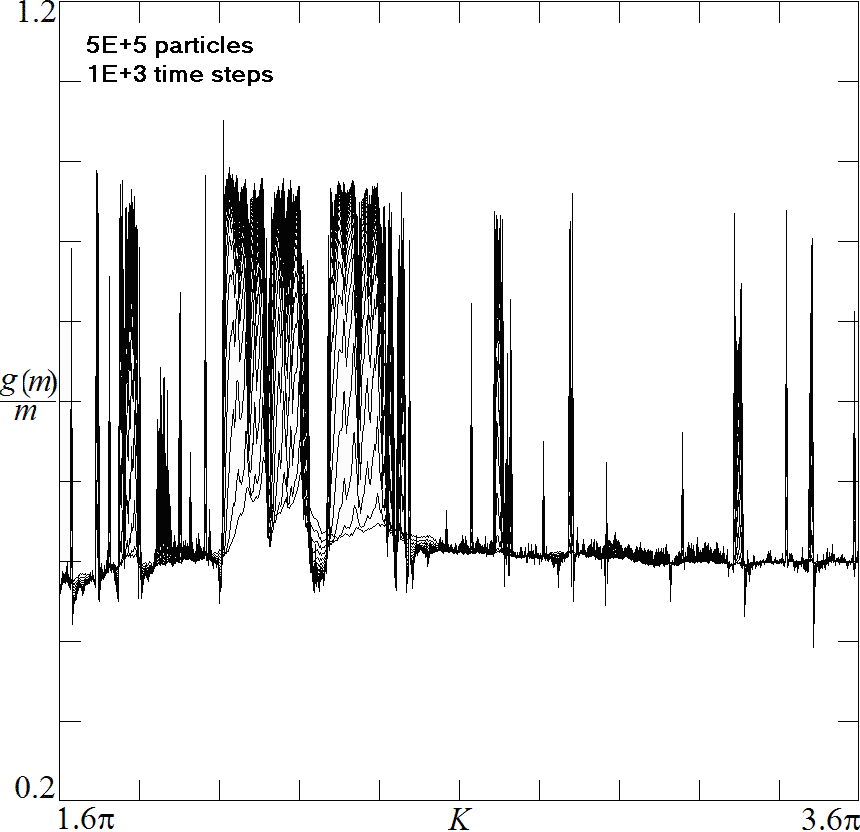
Fig. 3. Simple and anomalous scaling in the Chirikov map as a
function
of
m.
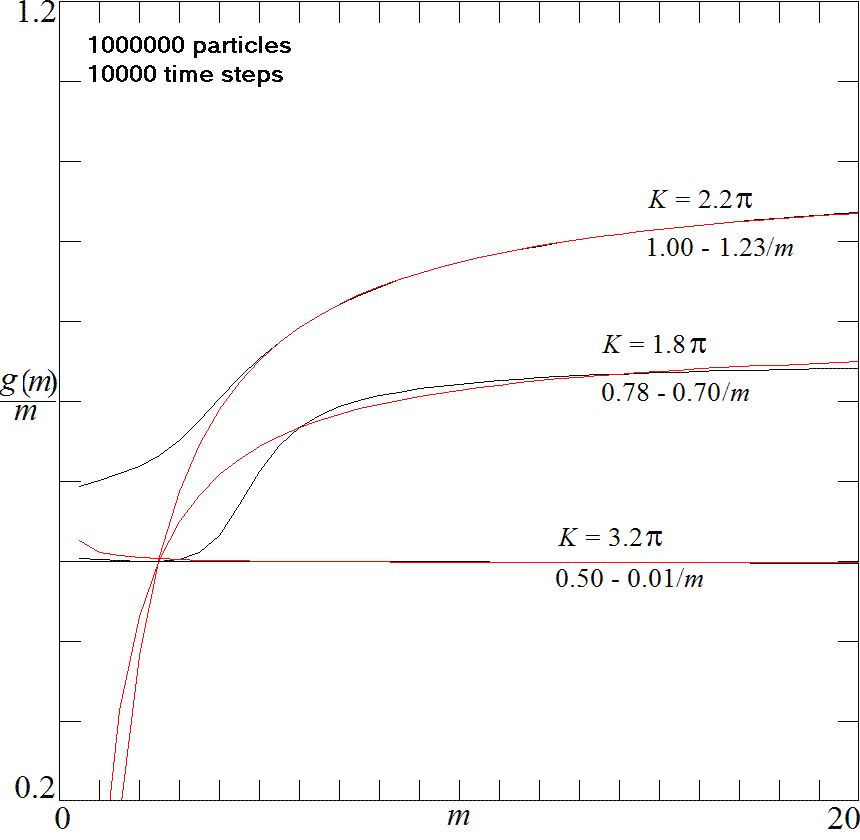
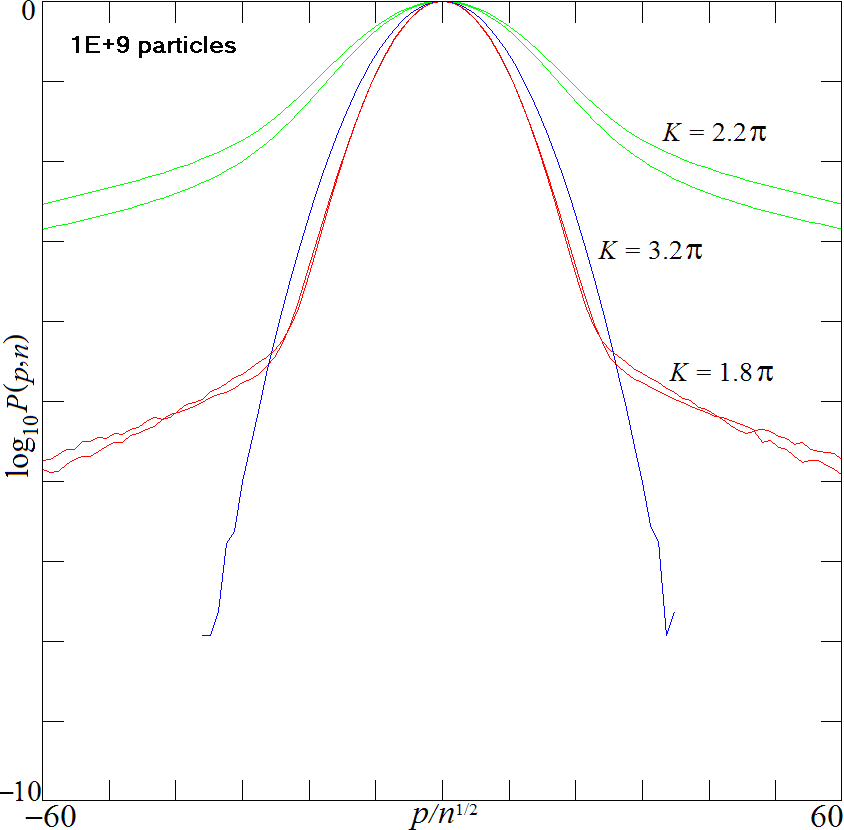
Fig. 4. Normalized PDF for the Chirikov map after 1000 iterations.
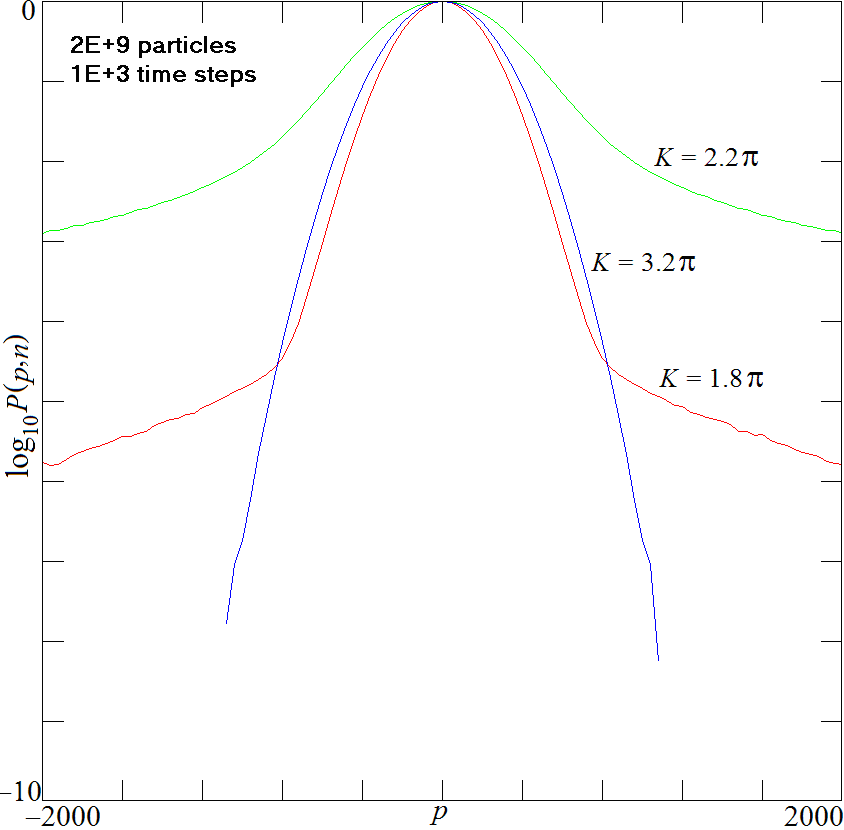
Fig. 5. The Weiss map for
k
=
0.4.
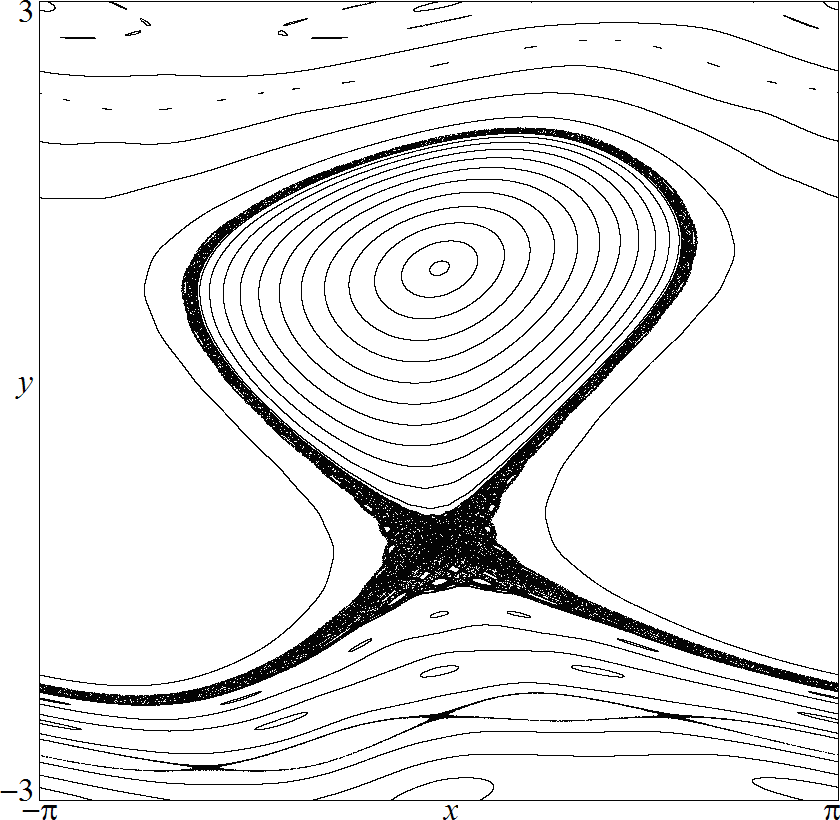
Fig. 6. Scaling of moments in the Weiss map as a function of
m.
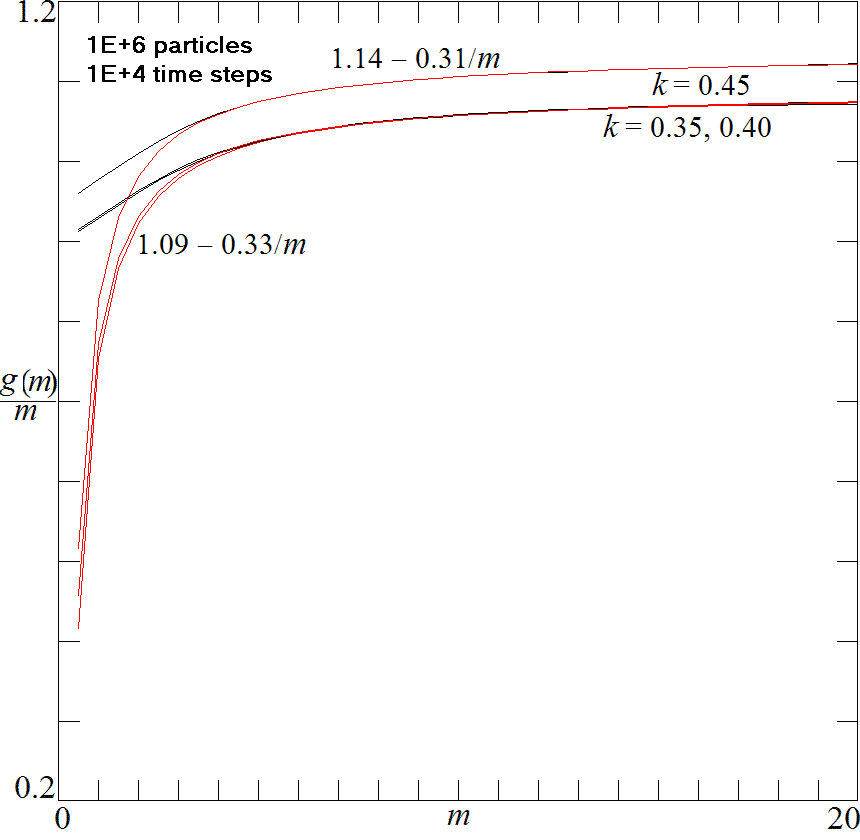
Fig. 7. Scaling of moments in the labyrinth model as a function of
m.
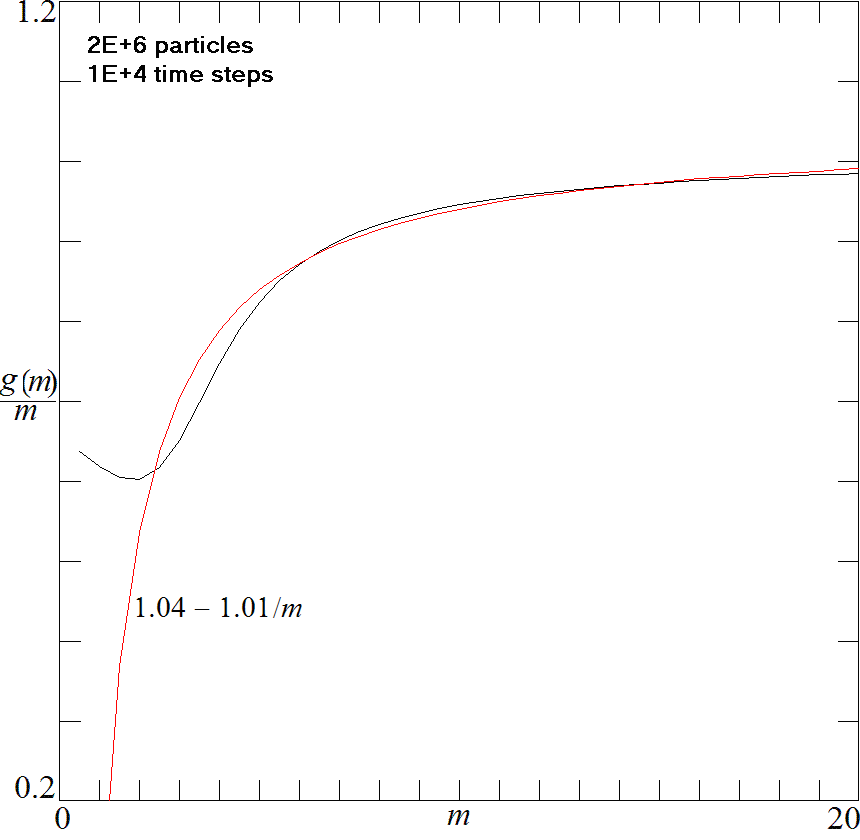
Fig. 8. Normalized PDFs for the Chirikov map at two different
times.