Chaotic Dynamics on Large Networks

J. C. Sprott
Departments of Physics, University of Wisconsin, Madison, WI 53706, USA

Received 30 March 2008; accepted 27 May 2008; published online 30 June 2008

ABSTRACT

Many systems in nature are governed by a large number of agents that interact nonlinearly through complex feedback loops. When the networks are sufficiently large and interconnected, they typically exhibit self-organization and chaos. This paper examines the prevalence and degree of chaos on large unweighted recurrent networks of ordinary differential equations with sigmoidal nonlinearities and unit coupling. The largest Lyapunov exponent is used as the signature and measure of the chaos, and the study includes the effects of damping, asymmetries in the distribution of coupling strengths, network symmetry, and sparseness of connections. Minimum conditions and optimal network architectures are determined for the existence of chaos. The results have implications for the design of social and other networks in the real world in which weak chaos is deemed desirable or as a way of understanding why certain networks might exist on “the edge of chaos.”

Ref: J. C. Sprott, Chaos 18, 023135-1 - 023135-9 (2008)

The complete paper is available in PDF format.

Return to Sprott's Books and Publications.

Fig. 1.
Fig. 1

Fig. 2.
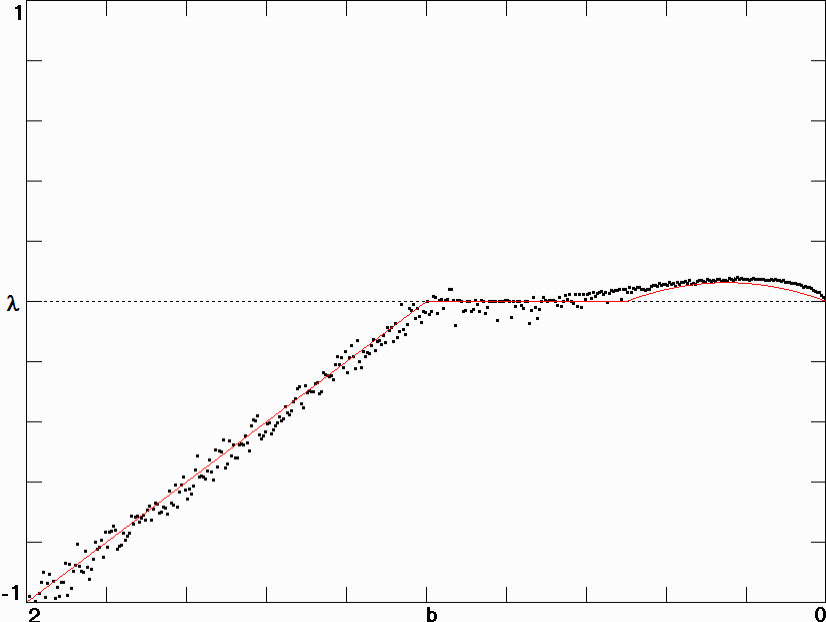
Fig. 2

Fig. 3.
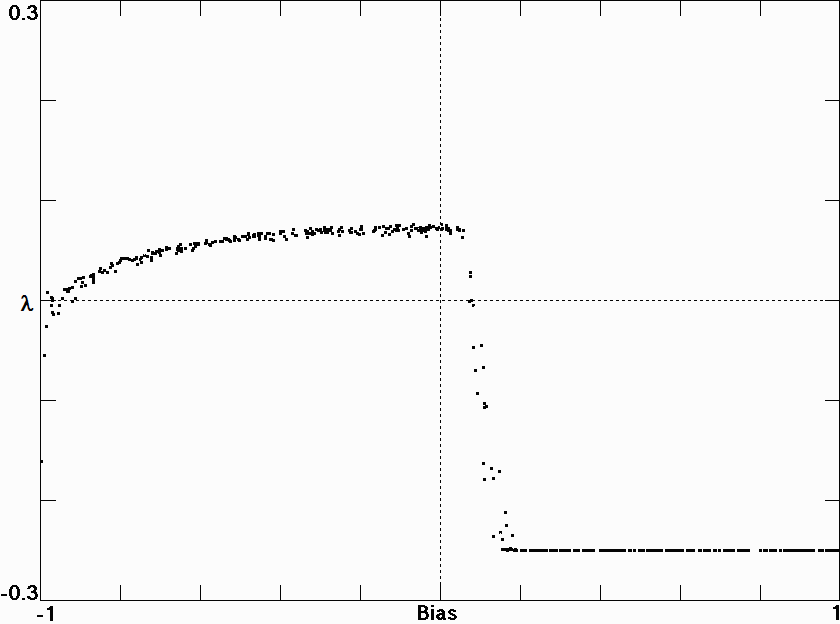
Fig. 3

Fig. 4.
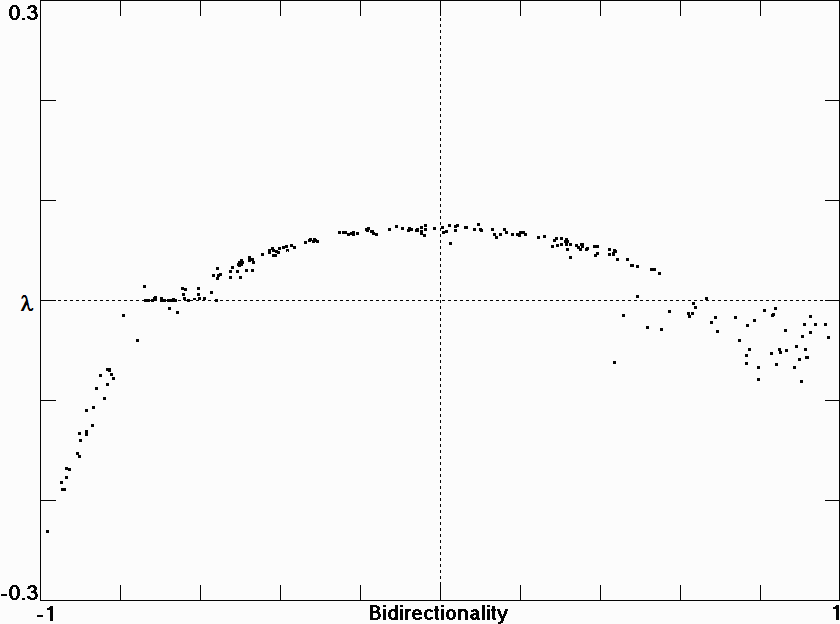
Fig. 4

Fig. 5.
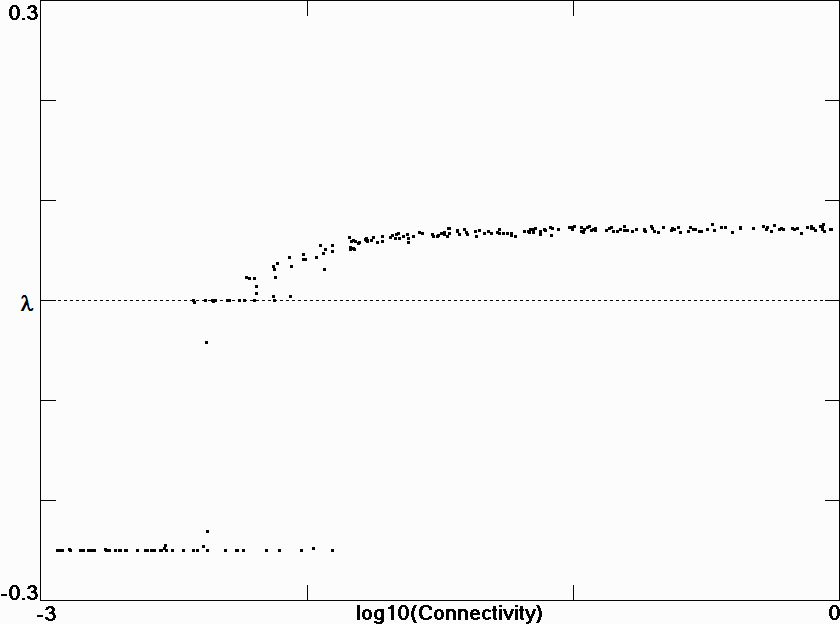
Fig. 5

Fig. 6.
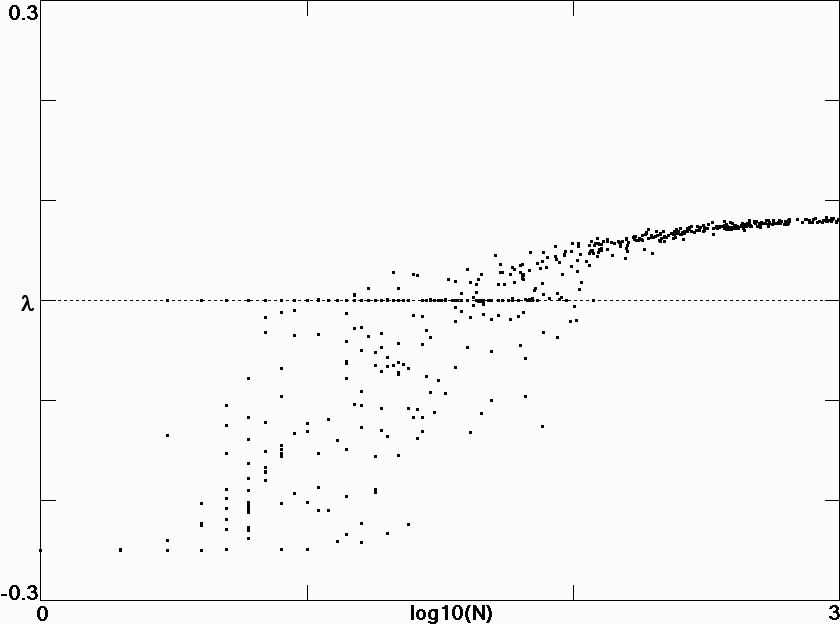
Fig. 6

Fig. 7.
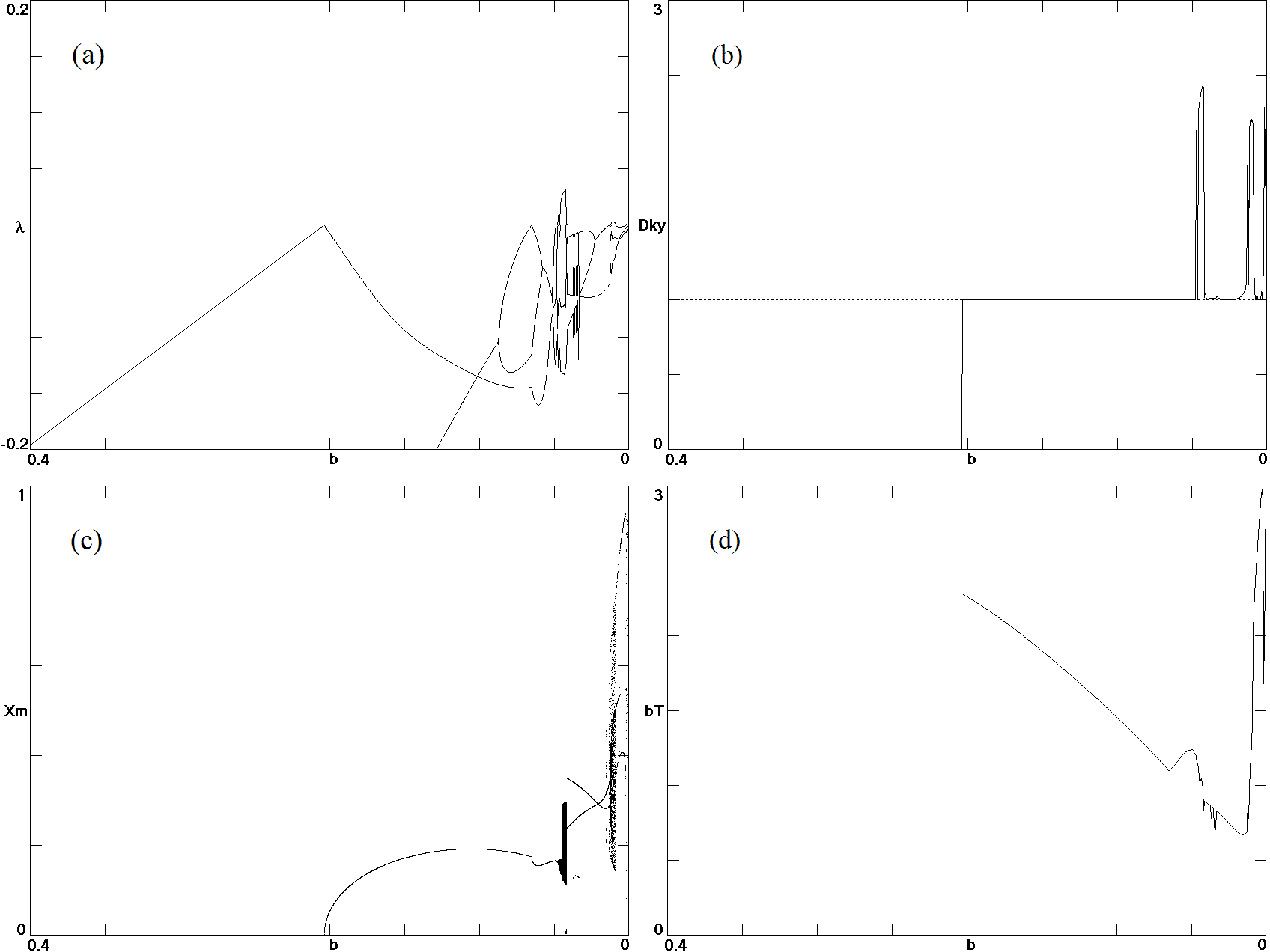
Fig. 7

Fig. 8.
Fig. 8

Fig. 9.
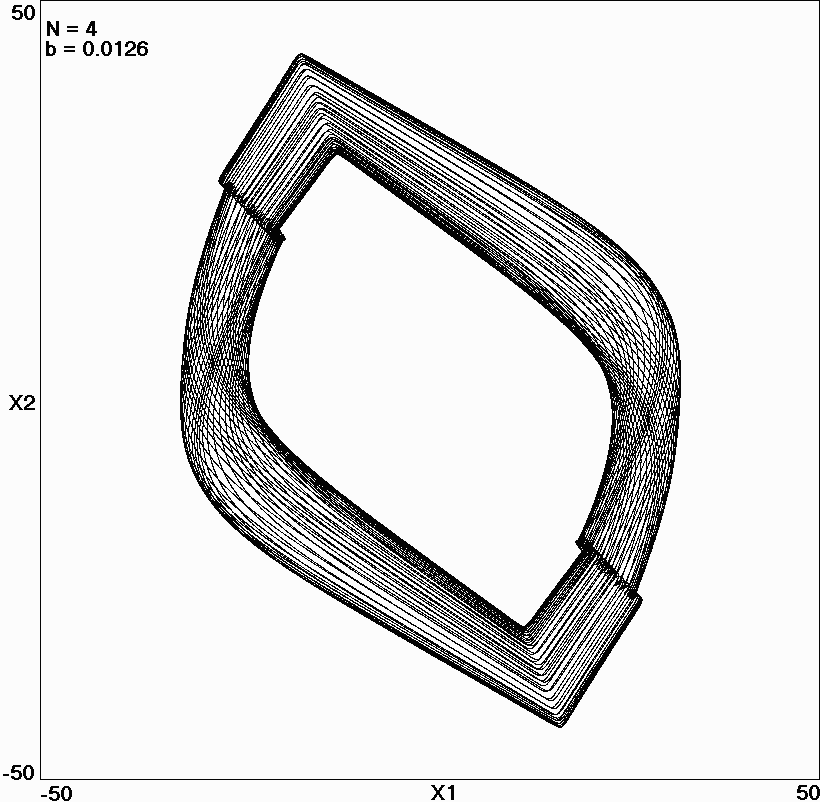
Fig. 9

Fig. 10.
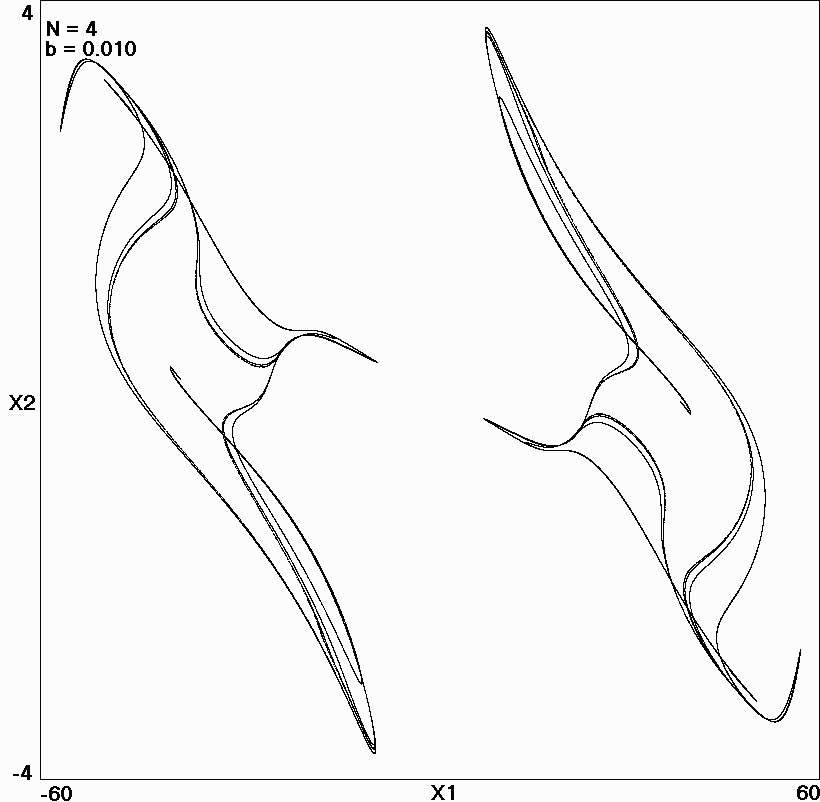
Fig. 10

Fig. 11.
Fig. 11

Fig. 12.
Fig. 12

Fig. 13.
Fig. 13

Fig. 14.
Fig. 14

Fig. 15.
Fig. 15

Fig. 16.
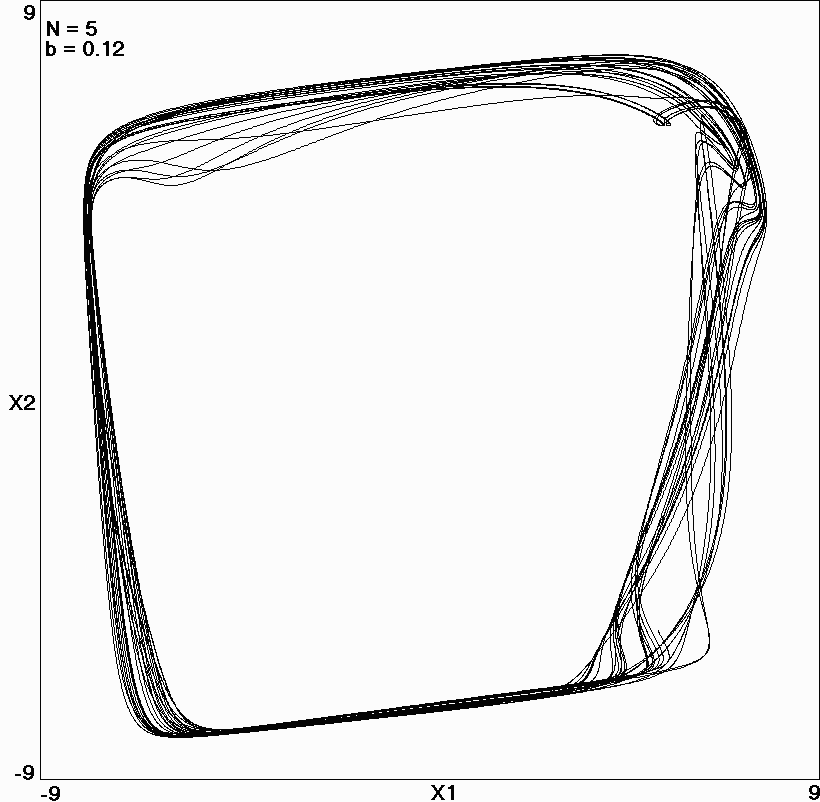
Fig. 16

Fig. 17.
Fig. 17

Fig. 18.
Fig. 18