
 Amazon.Com
and
Bn.Com Amazon.Com
and
Bn.Com

"Pickover contemplates realms beyond our known reality."
"Pickover inspires a new generation of da Vincis to build unknown flying machines and create new Mona Lisas."
|
From Pythagoras to the 57th Dimension,
|

|
I computed this "Word Cloud" from the book text. Click the image to magnify. I used this on-line tool to create the cloud.
P.S. The book itself unlocks the secrets of the Durer and Franklin magic squares that play a central role in Dan Brown's novel "The Lost Symbol." |

"Bucky Fuller thought big, Arthur C. Clarke thinks big, but Cliff Pickover outdoes them both." -- WIRED "A perpetual idea machine, Clifford Pickover is one of the most creative, original thinkers in the world today." -- Journal of Recreational Mathematics
|
 So many thought-provoking questions are posed and
answered in this beautifully illustrated book. Author
Clifford A. Pickover reveals the magic and mystery behind
some of the most significant mathematical milestones as well as the
oddest objects and ideas humanity has ever contemplated,
beginning in 150 million B.C. and ending with the latest
cutting-edge breakthroughs.
So many thought-provoking questions are posed and
answered in this beautifully illustrated book. Author
Clifford A. Pickover reveals the magic and mystery behind
some of the most significant mathematical milestones as well as the
oddest objects and ideas humanity has ever contemplated,
beginning in 150 million B.C. and ending with the latest
cutting-edge breakthroughs.
Mathematics has permeated every field of scientific endeavor. It can be used to explain the colors of the sunset or the architecture of our brains, and help us explore subatomic quantum realities and image faraway galaxies. Notable formulas and mathematical concepts are accompanied by fascinating facts about mathematicians' lives and real-world, practical applications of theorems. Journey with Pickover as he traces 250 achievements like ancient ant "odometers," the first abacus, the discovery of computer-generated fractals, and the quest for new dimensions. Here also are remarkable thinkers from Pythagoras and Euclid to modern-day math icon Martin Gardner and cosmologist Max Tegmark. Chronologically organized, each entry is short enough to digest in a few minutes and is presented along with a striking full-color image. "For me," writes Pickover, "mathematics cultivates a perpetual state of wonder about the nature of mind, the limits of thoughts, and our place in this vast cosmos."

|
 Enter a colorful, mathematical world filled with wonders and beauties.
Explore the mysteries of mathematics as the adventure unfolds over 1000s of years.
(Of course, the 100s of color images and mathematical milestones are credited and carefully described in the book.
Formulas, thought experiments, and recipes are given to allow thorough experimentation and deeper contemplation of the
famous puzzles, games, paradoxes, and formulations.) A special thanks to artists Paul Nylander, Teja Krasek, and Jos Leys. Here are just a few samples of the full-page images in the book:
Enter a colorful, mathematical world filled with wonders and beauties.
Explore the mysteries of mathematics as the adventure unfolds over 1000s of years.
(Of course, the 100s of color images and mathematical milestones are credited and carefully described in the book.
Formulas, thought experiments, and recipes are given to allow thorough experimentation and deeper contemplation of the
famous puzzles, games, paradoxes, and formulations.) A special thanks to artists Paul Nylander, Teja Krasek, and Jos Leys. Here are just a few samples of the full-page images in the book:
 Primates count |
 Cicada numbers |
 Platonic solids |
 Pappus hexagon |
 Abacus |
 Ganita math |
 Loxodrome |
 Holyhedron |
 Imaginary numbers |
 Boolean Algebra |
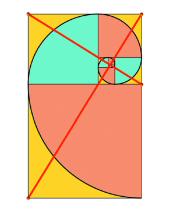 Golden ratio |
 Pseudosphere |
 Zermelo's choice |
 Langlands philos. |
 Hex game |
 Rubik's robot |





|
 Math's infinite mysteries and beauty unfold in this follow-up to the best-selling The Science Book. Beginning millions of years ago with ancient "ant odometers" and moving through time to our modern-day quest for new dimensions, it covers 250 milestones in mathematical history. Among the numerous delights readers will learn about as they dip into this inviting anthology: cicada-generated prime numbers, magic squares from centuries ago, the discovery of pi and calculus, and the butterfly effect. Each topic gets a lavishly illustrated spread with stunning color art, along with formulas and concepts, fascinating facts about scientists' lives, and real-world applications of the theorems.
Math's infinite mysteries and beauty unfold in this follow-up to the best-selling The Science Book. Beginning millions of years ago with ancient "ant odometers" and moving through time to our modern-day quest for new dimensions, it covers 250 milestones in mathematical history. Among the numerous delights readers will learn about as they dip into this inviting anthology: cicada-generated prime numbers, magic squares from centuries ago, the discovery of pi and calculus, and the butterfly effect. Each topic gets a lavishly illustrated spread with stunning color art, along with formulas and concepts, fascinating facts about scientists' lives, and real-world applications of the theorems.
Here is the Table of Contents for the book. How many of these entries are you familiar with? How many entries would you like to learn more about? |
 Introduction •
Ant Odometer (c. 150 million BC) •
Primates Count (c. 30 million BC) •
Cicada-Generated Prime Numbers (c. 1 million BC) •
Knots (c. 100,000 BC) •
Ishango Bone (c. 18,000 BC) •
Quipu (c. 3000 BC) •
Dice (c. 3000 BC) •
Magic Squares (c. 2200 BC) •
Plimpton 322 (c. 1800 BC) •
Rhind Papyrus (c. 1650 BC) •
Tic Tac Toe (c. 1300 BC) •
Pythagorean Theorem and Triangles (c. 600 BC) •
Go (548 BC) •
Pythagoras Founds Mathematical Brotherhood (530 BC) •
Zeno's Paradoxes (c. 445 BC) •
Quadrature of the Lune (c. 440 BC) •
Platonic Solids (350 BC) •
Aristotle's Organon (c. 350 BC) •
Aristotle's Wheel Paradox (c. 320 BC) •
Euclid's Elements (300 BC) •
Archimedes: Sand, Cattle & Stomachion (c. 250 BC) •
pi (c. 250 BC) •
Sieve of Eratosthenes (c. 240 BC) •
Archimedean Semi-Regular Polyhedra (c. 240 BC) •
Archimedes' Spiral (225 BC) •
Cissoid of Diocles (c. 180 BC) •
Ptolemy's Almagest (c. 150) •
Diophantus's Arithmetica (250) •
Pappus's Hexagon Theorem (c. 340) •
Bakhshali Manuscript (c. 350) •
The Death of Hypatia (415) •
Zero (c. 650) •
Alcuin's Propositiones ad Acuendos Juvenes (c. 800) •
al-Khwarizmi's Algebra (830) •
Borromean Rings (834) •
Ganita Sara Samgraha (850) •
Introduction •
Ant Odometer (c. 150 million BC) •
Primates Count (c. 30 million BC) •
Cicada-Generated Prime Numbers (c. 1 million BC) •
Knots (c. 100,000 BC) •
Ishango Bone (c. 18,000 BC) •
Quipu (c. 3000 BC) •
Dice (c. 3000 BC) •
Magic Squares (c. 2200 BC) •
Plimpton 322 (c. 1800 BC) •
Rhind Papyrus (c. 1650 BC) •
Tic Tac Toe (c. 1300 BC) •
Pythagorean Theorem and Triangles (c. 600 BC) •
Go (548 BC) •
Pythagoras Founds Mathematical Brotherhood (530 BC) •
Zeno's Paradoxes (c. 445 BC) •
Quadrature of the Lune (c. 440 BC) •
Platonic Solids (350 BC) •
Aristotle's Organon (c. 350 BC) •
Aristotle's Wheel Paradox (c. 320 BC) •
Euclid's Elements (300 BC) •
Archimedes: Sand, Cattle & Stomachion (c. 250 BC) •
pi (c. 250 BC) •
Sieve of Eratosthenes (c. 240 BC) •
Archimedean Semi-Regular Polyhedra (c. 240 BC) •
Archimedes' Spiral (225 BC) •
Cissoid of Diocles (c. 180 BC) •
Ptolemy's Almagest (c. 150) •
Diophantus's Arithmetica (250) •
Pappus's Hexagon Theorem (c. 340) •
Bakhshali Manuscript (c. 350) •
The Death of Hypatia (415) •
Zero (c. 650) •
Alcuin's Propositiones ad Acuendos Juvenes (c. 800) •
al-Khwarizmi's Algebra (830) •
Borromean Rings (834) •
Ganita Sara Samgraha (850) •
Thabit Formula for Amicable Numbers (c. 850) • Kitab al-fusul fi al-hisab al-Hindi (c. 953) • Omar Khayyam's Treatise (1070) • Al-Samawal's The Dazzling (c. 1150) • Abacus (c. 1200) • Fibonacci's Liber Abaci (1202) • Wheat on a Chessboard (1256) • Harmonic Series Diverges (c. 1350) • Law of Cosines (c. 1427) • Treviso Arithmetic (1478) • Discovery of Series Formula for Pi (c. 1500) • Golden Ratio (1509) • Polygraphiae Libri Sex (1518) • Loxodrome (1537) • Cardano's Ars Magna (1545) • Sumario Compendioso (1556) • Mercator Projection (1569) • Imaginary Numbers (1572) • Kepler Conjecture (1611) • Logarithms (1614) • Slide Rule (1621) • Fermat's Spiral (1636) • Fermat's Last Theorem (1637) • Descartes' La Geometrie (1637) • Cardioid (1637) • Logarithmic Spiral (1638) • Projective Geometry (1639) • Torricelli's Trumpet (1641) • Pascal's Triangle (1654) • The Length of Neile's Semicubical Parabola (1657) • Viviani's Theorem (1659) • Discovery of Calculus (c. 1665) • Newton's Method (1669) • Tautochrone Problem (1673) • Astroid (1674) •
 L'Hopital's Analysis of the Infinitely Small (1696) •
Rope around the Earth Puzzle (1702) •
Law of Large Numbers (1713) •
Euler's Number, e (1727) •
Stirling's Formula (1730) •
Normal Distribution Curve (1733) •
Euler-Mascheroni Constant (1735) •
Konigsberg Bridges (1736) •
St. Petersburg Paradox (1738) •
Goldbach Conjecture (1742) •
Agnesi's Instituzioni Analitiche (1748) •
Euler's Formula for Polyhedra (1751) •
Euler's Polygon Division Problem (1751) •
Knight's Tours (1759) •
Bayes' Theorem (1761) •
Franklin Magic Square (1769) •
Minimal Surface (1774) •
Buffon's Needle (1777) •
Thirty-Six Officers Problem (1779) •
Sangaku Geometry (c. 1789) •
Least Squares (1795) •
Constructing a Regular Heptadecagon (1796) •
Fundamental Theorem of Algebra (1797) •
Gauss's Disquisitiones Arithmeticae (1801) •
Three-Armed Protractor (1801) •
Fourier Series (1807) •
Laplace's Theorie Analytique des Probabilites (1812) •
Prince Rupert's Problem (1816) •
Bessel Functions (1817) •
Babbage Mechanical Computer (1822) •
Cauchy's Le Calcul Infinitesimal (1823) •
Barycentric Calculus (1827) •
Non-Euclidean Geometry (1829) •
Mobius Function (1831) •
Group Theory (1832) •
Pigeonhole Principle (1834) •
L'Hopital's Analysis of the Infinitely Small (1696) •
Rope around the Earth Puzzle (1702) •
Law of Large Numbers (1713) •
Euler's Number, e (1727) •
Stirling's Formula (1730) •
Normal Distribution Curve (1733) •
Euler-Mascheroni Constant (1735) •
Konigsberg Bridges (1736) •
St. Petersburg Paradox (1738) •
Goldbach Conjecture (1742) •
Agnesi's Instituzioni Analitiche (1748) •
Euler's Formula for Polyhedra (1751) •
Euler's Polygon Division Problem (1751) •
Knight's Tours (1759) •
Bayes' Theorem (1761) •
Franklin Magic Square (1769) •
Minimal Surface (1774) •
Buffon's Needle (1777) •
Thirty-Six Officers Problem (1779) •
Sangaku Geometry (c. 1789) •
Least Squares (1795) •
Constructing a Regular Heptadecagon (1796) •
Fundamental Theorem of Algebra (1797) •
Gauss's Disquisitiones Arithmeticae (1801) •
Three-Armed Protractor (1801) •
Fourier Series (1807) •
Laplace's Theorie Analytique des Probabilites (1812) •
Prince Rupert's Problem (1816) •
Bessel Functions (1817) •
Babbage Mechanical Computer (1822) •
Cauchy's Le Calcul Infinitesimal (1823) •
Barycentric Calculus (1827) •
Non-Euclidean Geometry (1829) •
Mobius Function (1831) •
Group Theory (1832) •
Pigeonhole Principle (1834) •
Quaternions (1843) • Transcendental Numbers (1844) • Catalan Conjecture (1844) • The Matrices of Sylvester (1850) • Four-Color Theorem (1852) • Boolean Algebra (1854) • Icosian Game (1857) • Harmonograph (1857) • The Mobius Strip (1858) • Holditch's Theorem (1858) • Riemann Hypothesis (1859) • Beltrami's Pseudosphere (1868) • Weierstrass Function (1872) • Gros's Theorie du Baguenodier (1872) • The Doctorate of Kovalevskaya (1874) • Fifteen Puzzle (1874) • Cantor's Transfinite Numbers (1874) • Reuleaux Triangle (1875) • Harmonic Analyzer (1876) • Ritty Model I Cash Register (1879) • Venn Diagrams (1880) • Benford's Law (1881) • Klein Bottle (1882) • Tower of Hanoi (1883) • Flatland (1884) • Tesseract (1888) • Peano Axioms (1889) • Peano Curve (1890) • Wallpaper Groups (1891) • Sylvester's Line Problem (1893) • Proof of the Prime Number Theorem (1896) • Pick's Theorem (1899) • Morley's Trisector Theorem (1899) • Hilbert's 23 Problems (1900) • Chi-Square (1900) • Boy's Surface (1901) •
 Barber Paradox (1901) •
Jung's Theorem (1901) •
Poincare Conjecture (1904) •
Koch Snowflake (1904) •
Zermelo's Axiom of Choice (1904) •
Jordan Curve Theorem (1905) •
Thue-Morse Sequence (1906) •
Brouwer Fixed-Point Theorem (1909) •
Normal Number (1909) •
Boole's Philosophy and Fun of Algebra (1909) •
Principia Mathematica (1910-1913) •
Hairy Ball Theorem (1912) •
Infinite Monkey Theorem (1913) •
Bieberbach Conjecture (1916) •
Johnson's Theorem (1916) •
Hausdorff Dimension (1918) •
Brun's Constant (1919) •
Googol (c. 1920) •
Antoine's Necklace (1920) •
Noether's Idealtheorie (1921) •
Lost in Hyperspace (1921) •
Geodesic Dome (1922) •
Alexander's Horned Sphere (1924) •
Banach-Tarski Paradox (1924) •
Squaring a Rectangle (1925) •
Hilbert's Grand Hotel (1925) •
Menger Sponge (1926) •
Differential Analyzer (1927) •
Ramsey Theory (1928) •
Godel's Theorem (1931) •
Champernowne's Number (1933) •
Bourbaki: Secret Society (1935) •
Fields Medal (1936) •
Turing Machines (1936) •
Voderberg Tilings (1936) •
Collatz Conjecture (1937) •
Barber Paradox (1901) •
Jung's Theorem (1901) •
Poincare Conjecture (1904) •
Koch Snowflake (1904) •
Zermelo's Axiom of Choice (1904) •
Jordan Curve Theorem (1905) •
Thue-Morse Sequence (1906) •
Brouwer Fixed-Point Theorem (1909) •
Normal Number (1909) •
Boole's Philosophy and Fun of Algebra (1909) •
Principia Mathematica (1910-1913) •
Hairy Ball Theorem (1912) •
Infinite Monkey Theorem (1913) •
Bieberbach Conjecture (1916) •
Johnson's Theorem (1916) •
Hausdorff Dimension (1918) •
Brun's Constant (1919) •
Googol (c. 1920) •
Antoine's Necklace (1920) •
Noether's Idealtheorie (1921) •
Lost in Hyperspace (1921) •
Geodesic Dome (1922) •
Alexander's Horned Sphere (1924) •
Banach-Tarski Paradox (1924) •
Squaring a Rectangle (1925) •
Hilbert's Grand Hotel (1925) •
Menger Sponge (1926) •
Differential Analyzer (1927) •
Ramsey Theory (1928) •
Godel's Theorem (1931) •
Champernowne's Number (1933) •
Bourbaki: Secret Society (1935) •
Fields Medal (1936) •
Turing Machines (1936) •
Voderberg Tilings (1936) •
Collatz Conjecture (1937) •
Ford Circles (1938) • The Rise of Randomizing Machines (1938) • Birthday Paradox (1939) • Polygon Circumscribing (c. 1940) • Hex (1942) • Pig Game Strategy (1945) • ENIAC (1946) • Von Neumann's Middle-Square Randomizer (1946) • Gray Code (1947) • Information Theory (1948) • Curta Calculator (1948) • Csaszar Polyhedron (1949) • Nash Equilibrium (1950) • Coastline Paradox (c. 1950) • Prisoner's Dilemma (1950) • Cellular Automata (1952) • Martin Gardner's Mathematical Recreations (1957) • Gilbreath's Conjecture (1958) • Turning a Sphere Inside Out (1958) • Platonic Billiards (1958) • Outer Billiards (1959) • Newcomb's Paradox (1960) • Sierpinski Numbers (1960) • Chaos and the Butterfly Effect (1963) • Ulam Spiral (1963) • Continuum Hypothesis Undecidability (1963) • Superegg (c. 1965) • Fuzzy Logic (1965) • Instant Insanity (1966) • Langlands Program (1967) • Sprouts (1967) • Catastrophe Theory (1968) • Tokarsky's Unilluminable Room (1969) • Donald Knuth and Mastermind (1970) • Erdos and Extreme Collaboration (1971) • HP-35: First Scientific Pocket Calculator (1972) •
 Penrose Tiles (1973) •
Art Gallery Theorem (1973) •
Rubik's Cube (1974) •
Chaitin's Omega (1974) •
Surreal Numbers (1974) •
Perko Knots (1974) •
Fractals (1975) •
Feigenbaum Constant (1975) •
Public-Key Cryptography (1977) •
Szilassi Polyhedron (1977) •
Ikeda Attractor (1979) •
Spidrons (1979) •
Mandelbrot Set (1980) •
Monster Group (1981) •
Ball Triangle Picking (1982) •
Jones Polynomial (1984) •
Weeks Manifold (1985) •
Andrica's Conjecture (1985) •
The ABC Conjecture (1985) •
Audioactive Sequence (1986) •
Mathematica (1988) •
Murphy's Law and Knots (1988) •
Butterfly Curve (1989) •
The On-Line Encyclopedia of Integer Sequences (1996) •
Eternity Puzzle (1999) •
Perfect Magic Tesseract (1999) •
Parrondo's Paradox (1999) •
Solving of the Holyhedron (1999) •
Bed Sheet Problem (2001) •
Solving the Game of Awari (2002) •
Tetris is NP-Complete (2002) •
NUMB3RS (2005) •
Checkers is Solved (2007) •
The Quest for Lie Group E8 (2007) •
Mathematical Universe Hypothesis (2007) •
Notes and Further Reading •
About the Author
Penrose Tiles (1973) •
Art Gallery Theorem (1973) •
Rubik's Cube (1974) •
Chaitin's Omega (1974) •
Surreal Numbers (1974) •
Perko Knots (1974) •
Fractals (1975) •
Feigenbaum Constant (1975) •
Public-Key Cryptography (1977) •
Szilassi Polyhedron (1977) •
Ikeda Attractor (1979) •
Spidrons (1979) •
Mandelbrot Set (1980) •
Monster Group (1981) •
Ball Triangle Picking (1982) •
Jones Polynomial (1984) •
Weeks Manifold (1985) •
Andrica's Conjecture (1985) •
The ABC Conjecture (1985) •
Audioactive Sequence (1986) •
Mathematica (1988) •
Murphy's Law and Knots (1988) •
Butterfly Curve (1989) •
The On-Line Encyclopedia of Integer Sequences (1996) •
Eternity Puzzle (1999) •
Perfect Magic Tesseract (1999) •
Parrondo's Paradox (1999) •
Solving of the Holyhedron (1999) •
Bed Sheet Problem (2001) •
Solving the Game of Awari (2002) •
Tetris is NP-Complete (2002) •
NUMB3RS (2005) •
Checkers is Solved (2007) •
The Quest for Lie Group E8 (2007) •
Mathematical Universe Hypothesis (2007) •
Notes and Further Reading •
About the Author
|
The Math Book features both the Rubik's Cube and the fractal Menger Sponge.
Here is a Menger sponge:

My favorite combination of the Rubik's Cube and Menger Sponge, far too difficult for any human to solve, is the "Menger Rubik's Cube," pictured at right, by Petter Duvander. You can learn more about this "Mengerubik Cubesponge" here. Imagine a race of mathematician aliens attempting to solve the Cube at all size scales. Imagine walking with someone you love along its hidden and mysterious interstices.
Book Reviews"I have often said that a good book is not merely written or compiled, it is crafted. That is, the book is designed for a specific audience and the textual and sensory format is carefully chosen for that audience. Clifford Pickover’s latest venture into the history of mathematics is such an endeavor. This is a wonderful book... excellent, stimulating and inspiring.... Highly recommended.... a tour de force of mathematical ideas" -- Frank J. Swetz, Mathematical Association of America - Book review at The Australian: "Clifford A. Pickover is author of more books than there are decimal places in pi. As his title suggests, Pickover, well, picks over all the best numerical oddities in chronological order, beginning at 150 million BC with the development of the odometer by ants... My longtime rave fave is the Mobius strip…. Small children and the inebriated will be amazed." - Leigh Dayton, The Australian (newspaper)
- Radio interview at Math Factor - Book review at Midwest Book Review: "Amazing.... gorgeous.... fascinating.... thoroughly enjoyable.... beautiful.... fun!
- Book review at Seed Magazine:
"Handsome, image-filled volume.... Pickover, a bona fide polymath who has written more than 40 books, elegantly sums up each mathematical feat...
Entertaining introduction to many strange and surprising ideas....
The book lets readers glimpse the history and development of mathematics and leaves a sense of awe at just how far the field has come." - Book review at Boing Boing: "A palace filled with awe-inspiring curiosities...." - Book review at Neatorama: "A thoroughly enjoyable walk through the history of mathematics with each milestone narrated by Pickover in a short and sweet fashion..." - Book review at Political: "Clifford... sees patterns in everything he looks at, and thinks in logical ways that the average person would scratch their head about. Some could call a man like Clifford obsessed. Whatever he is, his research is impeccable." - Book review at Dr. Dobbs: Delightful…. a truly enjoyable read, approachable by anyone with a curiosity of how numbers have shaped the world we live in…. Beautiful… clear, stunning… Permits the concepts to percolate, savored and appreciated. This is unlike any math book I've read before. There are so many unique facts and stories collected in this work that it demands to be re-read. The educational journey it offers is so memorable and rewarding…. The Math Book would make a memorable gift for any person in a technical field (especially in the realm of computers). I highly recommend this book and look forward to future compilations that Dr. Pickover may have on the horizon. "A marvelous popular trot through some 250 great mathematical conundrums.... with wonderfully exotic names such as the Quadrature of the Lune, Borromean Rings, and Fermat's Spiral." --Sydney Morning Herald "Clifford Pickover’s enthusiasm for all things mathematical is contagious! And each page of this stunning gift book is a testament to the sheer beauty—both intellectual and aesthetic— of the field as seen through his eyes. From evidence of a built-in “pedometer” in an ancient species of ant (dating from more than 150 million years ago) to the Mathematical Universe Hypothesis (advanced in 2007), this chronologically organized tour through “250 milestones in the history of mathematics” provides a concise explanation of the featured theorem/formula/discovery alongside a colorfully evocative illustration. The perfect present for mathematicians and number crunchers, The Math Book also offers an accessible and inspiring survey of major mathematical concepts—and their real-world relevance—for English-major types." - Bas Bleu "Pickover has scoured the millennia and the universe for milestones in maths, and has produced a thought-provoking and entertaining book." -- The Newcastle Herald. Nice entry for The Math Book in the "Signals" gift catalogue, along with math mug. |

Petter Duvander's "Menger Rubik's Cube,"
|
 I've
compiled the following list that identifies some of the material I used to
research and write this book. Occasionally, I also provide a few extra notes
(♪) of clarification in this section, which includes information culled from
books, journals and Web sites. As many
readers are aware, Internet Web sites come and go. Sometimes they change
addresses or completely disappear. The
Web site addresses listed here provided valuable background information when
this book was written. You can, of
course, find numerous other web sites relating to these mathematical marvels
and milestones using standard Web search tools.
I've
compiled the following list that identifies some of the material I used to
research and write this book. Occasionally, I also provide a few extra notes
(♪) of clarification in this section, which includes information culled from
books, journals and Web sites. As many
readers are aware, Internet Web sites come and go. Sometimes they change
addresses or completely disappear. The
Web site addresses listed here provided valuable background information when
this book was written. You can, of
course, find numerous other web sites relating to these mathematical marvels
and milestones using standard Web search tools.
 If I have overlooked an interesting or
pivotal moment in mathematics that you feel has never been fully appreciated,
please let me know about it. Just visit my web site pickover.com, and send me
an e-mail explaining the idea and how you feel it influenced the mathematical
world. Perhaps future editions of the
book will include mathematical marvels such as: (1) the Gomboc, a special kind
of three-dimensional object that always tips itself back into a "standing"
position as if by magic, (2) the ancient Chinese texts The Nine Chapters on
the Mathematical Art and The Suan Shu Shū (Writings on
Reckoning), the later of which was written on 190 bamboo strips, (3) the Frobenius postage stamp problem, posed by English
mathematician James Sylvester in 1884 as a money-changing problem, (4) tangram
dissection puzzles, and (5) the ideas of Sophie Germain, one of the great
mathematicians of the early 19th century who considered topics related
to Fermat's Last Theorem and other areas in number theory.
If I have overlooked an interesting or
pivotal moment in mathematics that you feel has never been fully appreciated,
please let me know about it. Just visit my web site pickover.com, and send me
an e-mail explaining the idea and how you feel it influenced the mathematical
world. Perhaps future editions of the
book will include mathematical marvels such as: (1) the Gomboc, a special kind
of three-dimensional object that always tips itself back into a "standing"
position as if by magic, (2) the ancient Chinese texts The Nine Chapters on
the Mathematical Art and The Suan Shu Shū (Writings on
Reckoning), the later of which was written on 190 bamboo strips, (3) the Frobenius postage stamp problem, posed by English
mathematician James Sylvester in 1884 as a money-changing problem, (4) tangram
dissection puzzles, and (5) the ideas of Sophie Germain, one of the great
mathematicians of the early 19th century who considered topics related
to Fermat's Last Theorem and other areas in number theory.
 General
Reading
General
Reading
Anderson, Marlow, Victor Katz, and Robin
Wilson, Sherlock Holmes in
Boyer, Carl B. and Uta C. Merzbach, A History of Mathematics (Hoboken, New Jersey: John Wiley & Sons, 1991).
Darling, David, The Universal Book of Mathematics (
Dunham, William, Journey through Genius: The Great Theorems of Mathematics (New York: Penguin, 1991).
Gardner, Martin, Martin Gardner's
Mathematical Games (CD-ROM) (
Gullberg, Jan, Mathematics: From the Birth of Numbers (New York: W. W. Norton, 1997).
Hawking, Stephen, God Created the
Integers: The Mathematical Breakthroughs That Changed History (
Hodgkin, Luke, A History of
Mathematics: From Mesopotamia to Modernity (
O'Connor, John J., and Robertson, Edmund
F., "The MacTutor History of Mathematics Archive,"
Pickover, Clifford, A Passion
for Mathematics (
Weisstein, Eric, "MathWorld: a Wolfram web resource"; see http://mathworld.wolfram.com/.
Wikipedia Encyclopedia; see http://www.wikipedia.org/.
 Introduction
Introduction
♪ Many scholars have noted that Galileo's "La matematica è l'alfabeto nel quale Dio ha scritto l'universo" may be translated as "Mathematics is the alphabet with which God has written the Universe."
When I employ the term "whole number" in the Introduction, I use it to refer to all the integers, although some authors have restricted its meaning to the nonnegative integers.
Devlin Keith, "Devlin's Angle:
What Can Mathematics Do for the Businessperson?" The Mathematical Association
of
Devlin Keith, "Devlin's Angle: Naming Theorems," The
Mathematical Association of
Dorrie, Heinrich, 100 Great Problems of Elementary Mathematics: Their History and Solution (New York, Dover, 1965).
Ifrah, Georges, The Universal History of Numbers (Hoboken, New Jersey: John Wiley & Sons, 1999).
Kaku, Michio, Hyperspace (New York: Anchor, 1995).
Kammerer, Paul, Das Gesetz der Serie (The Law of Seriality) (Stuttgart: Deutsche Verlags-Anstalt, 1919).
Klarreich, Erica, "Math Lab:
Computer Experiments are Transforming Mathematics," Science News,
165(17): 266-268,
Kruglinski, Susan, "When Even
Mathematicians Don't Understand the Math," The New York Times,
Pickover, Clifford, Wonders of
Numbers (
Pickover, Clifford, Calculus
and Pizza (
Pickover, Clifford, A Passion
for Mathematics (
Pickover, Clifford, The
Mobius Strip (
Pickover, Clifford, From
Archimedes to Hawking (
 Ant
Odometer (c. 150 million BC)
Ant
Odometer (c. 150 million BC)
Devlin, Keith, "The Amazing Ahmed," December, 2004, The Mathematical Association of America; see http://www.maa.org/devlin/devlin_12_04.html.
Wehner, Rüdiger and Mandyam V. Srinivasan, "Searching Behavior of Desert Ants, Genus Cataglyphis (Formicidae, Hymenoptera), Journal of Comparative Physiology A: Neuroethology, Sensory, Neural, and Behavioral Physiology, 142(3): 315-338, (September, 1981).
Wittlinger, Matthias, Rüdiger Wehner, and Harald Wolf, "The Ant Odometer: Stepping on Stilts and Stumps," Science, 312(5782): 1965 – 1967 (June, 2006).
Wohlgemuth, Sandra, Bernhard Ronacher, and Rüdiger Wehner, "Ant Odometry in the Third Dimension, Nature 411(6839): 795-798 (2001).
 Primates Count (c. 30 million BC)
Primates Count (c. 30 million BC)
Beran, Michael, "Long-term retention of the differential values of Arabic numerals by chimpanzees (Pan troglodytes)," Animal Cognition, 7(2): 86-92 (April, 2004).
"Chimps Remember How to Play the Numbers Game
for Years," New Scientist, 180(2421): 16 (
Kalmus, H., "Animals as Mathematicians," Nature 202:
1156-1160 (
Matsuzawa, Tetsuro, "Use of Numbers
by a Chimpanzee," Nature, 315: 57-59 (
Pickover, Clifford, A Passion
for Mathematics (
 Cicada-Generated Prime Numbers (c. 1 million BC)
Cicada-Generated Prime Numbers (c. 1 million BC)
Campos, Paulo R. A., Viviane M. de Oliveira, Ronaldo Giro, and Douglas S. Galvao, "Emergence of Prime Numbers as the Result of Evolutionary Strategy," Physical Review Letters 93(9): 098107-1 - 098107-4 (August, 2004).
Cox, Randel Tom, and C. E. Carlton. "A commentary on Prime Numbers and Life Cycles of Periodical Cicadas," American Naturalist, 152(1): 162–164 (1988).
Goles, Eric, Oliver Schulz, and Mario Markus, "A Biological Generator of Prime Numbers," Nonlinear Phenomena in Complex Systems, 3(2): 208–21 (2000).
Hayes, Brian, "Bugs that Count," American Scientist, 92(5): 401-405 (September, 2004); see http://www.americanscientist.org/template/AssetDetail/assetid/35547.
Peterson, Ivars, "Prime-Time Cicadas," Sciences News (online), 163(25), June 2003; see http://sciencenewsmagazine.org/articles/20030621/mathtrek.asp.
Stroh, Michael, "Mathematicians Explore Cicada's Mysterious
Link with Primes," Baltimore
Sun,
 Knots (c. 100,000 BC)
Knots (c. 100,000 BC)
♪ Animals formed knots long before humans. For example, Gordian knot worms (phylum Nematomorpha) are well known for contorting themselves into knots, with one or more worms tangled together.
Sher, R. B., "Max Dehn and
Bouzouggar, Abdeljalil, Nick Barton, Marian Vanhaeren,
Francesco d'Errico, Simon Collcutt, Tom Higham, Edward Hodge, Simon Parfitt,
Edward Rhodes Jean-Luc Schwenninger, Chris Stringer, Elaine Turner, Steven
Ward, Abdelkrim Moutmir, and Abdelhamid Stambouli, "82,000-Year-Old Shell Beads
from North Africa and Implications for the Origins Of Modern Human Behavior," Proc.
Natl. Acad. Sci., 104 (24):| 9964-9969 (
Leys, Jos, "Mathematical Imagery by Jos Leys"; see http://www.josleys.com/galleries.php.
Meehan, Bernard, The Book of Kells: An Illustrated Introduction to the Manuscript (London: Thames & Hudson, 1994).
Pickover, Clifford, The
Mobius Strip (
Sossinsky, Alexi, Knots (
 Ishango Bone (c. 18,000 BC)
Ishango Bone (c. 18,000 BC)
Bogoshi, Jonas, Kevin Naidoo, and John Webb, "The Oldest Mathematical Artifact," Mathematical Gazette, 71(458): 294 (1987).
Teresi, Dick, Lost Discoveries:
The Ancient Roots of Modern Science (
Quipu (c. 3000 BC)
Ascher, Marcia and Robert Ascher, Mathematics of the Incas: Code of the Quipu (New York: Dover, 1997).
Mann,
Charles, "Unraveling Khipu's Secrets" Science, 309(5737): 1008-1009 (
Salomon,
Frank. The Cord Keepers: Khipus and Cultural Life in a
 Dice (c. 3000 BC)
Dice (c. 3000 BC)
♪ The term "random numbers" is used as a shorthand for the more precise term "pseudo-random numbers." Sequences such as the results of an ideal die roll exhibit statistical randomness.
Hawking, Stephen and Roger Penrose, The Nature of Space and Time (Princeton, New Jersey: Princeton University Press, 1996).
Hayes, Brian, "Randomness as a Resource," American Scientist 89(4): 300-304 (July-August 2001); see http://www.americanscientist.org/template/AssetDetail/assetid/20829/.
Knizia, Reiner, Dice Games Properly Explained (London: Elliot Right Way Books, 1999).
 Magic Squares (c. 2200 BC)
Magic Squares (c. 2200 BC)
Andrews, W. S., Magic Squares and Cubes (New York: Dover, 1960), originally printed in 1917.
Gardner, Martin, Time Travel and other Mathematical Bewilderments (New York: Freeman: 1987).
Pickover, Clifford, The Zen
of Magic Squares, Circles, and Stars (
 Plimpton 322 (c. 1800 BC)
Plimpton 322 (c. 1800 BC)
Robson, Eleanor, "Words and pictures: new light on Plimpton 322," American Mathematical Monthly 109(2): 105–120 (2002).
Friberg, Joran, Amazing Traces
of a Babylonian Origin in Greek Mathematics (River Edge,
 Rhind Papyrus (c. 1650 BC)
Rhind Papyrus (c. 1650 BC)
Eves, Howard Whitley, Great Moments in Mathematics (Before 1650) (Washington, DC: Mathematical Association of America, 1983).
Robins, Gary and Charles Shute, The Rhind Mathematical Papyrus: An Ancient Egyptian Text (New York: Dover, 1990).
 Tic Tac Toe (c. 1300 BC)
Tic Tac Toe (c. 1300 BC)
♪ Claudia Zaslavasky notes that a 3,300-year-old temple to the memory of Pharaoh Seti I has a tic-tac-toe-like board carved into it, along with other apparent game boards. David Darling suggests that the actual modern rules of tic tac toe were first described by Charles Babbage around 1820.
Claudia Zaslavasky's Tic Tac Toe and Other Three-In-A-Row Games (New York: Thomas Crowell, 1982).
Darling, David, The Universal Book of Mathematics (
 Pythagorean Theorem and Triangles (c. 600 BC)
Pythagorean Theorem and Triangles (c. 600 BC)
Beiler, Albert, Recreations in the Theory of Numbers (New York: Dover, 1964).
Loomis, Elisha Scott, Pythagorean Proposition (Washington, D.C.: National Council of Teachers of Mathematics, 1972), reprint of a book with first and second editions published in 1927 and 1940, respectively.
Maor, Eli, The Pythagorean
Theorem: A 4,000-Year History (
 Go (548 BC)
Go (548 BC)
Frankel, Karen, "Silicon Smackdown: New Go Algorithm Aims to Depose Humans," Scientific American, 296(6): 32-33 (June 2007).
Shotwell, Peter, Huiren Yang, and Sangit Chatterjee, Go:
More Than a Game (North
 Pythagoras Founds Mathematical Brotherhood (530 BC)
Pythagoras Founds Mathematical Brotherhood (530 BC)
♪ Philosopher Bertrand Russell once wrote that Pythagoras was intellectually one of the most important men that ever lived, both when he was wise and when he was unwise. Pythagoras was the most puzzling mathematician of history because he founded a numerical religion whose main tenants were transmigration of souls and the sinfulness of eating beans, along with a host of other odd rules and regulations.
According to Jim Holt, "Mathematicians believe in God at a rate two and a half times that of biologists.… Most mathematicians believe in heaven. Not a heaven with angels, but one populated by the abstract objects they devote themselves to studying: perfect spheres, infinite numbers, the square root of minus one and the like. Moreover, they believe they commune with this realm of timeless entities through a sort of extrasensory perception. Mathematicians who buy into this fantasy are called ‘Platonists'."
Gorman, Peter, Pythagoras: A Life (London: Routledge Kegan & Paul, 1978).
Holt, Jim, "Proof," The New York Times
Books Review,
Pickover, Clifford, The Loom of God (New York: Plenum, 1997).
Russell, Bertrand, A History of Western Philosophy (New York: Simon and Schuster, 1945).
 Zeno's Paradoxes (c. 445 BC)
Zeno's Paradoxes (c. 445 BC)
Mazur, Joseph, The Motion
Paradox: The 2,500-Year Old Puzzle Behind All the Mysteries of Time and
Space (
McLaughlin, William, "Resolving Zeno's Paradoxes," Scientific American, 271(5): 84-89 (November, 1994).
 Quadrature of the Lune (c. 440 BC)
Quadrature of the Lune (c. 440 BC)
Dunham, William, Journey through Genius: The Great Theorems of Mathematics (New York: Penguin, 1991).
Heilbron, J. L., "Quadrature of the Lune," Encyclopædia Britannica; see http://www.britannica.com/eb/article-9126480.
 Platonic Solids (c. 350 BC)
Platonic Solids (c. 350 BC)
♪ Platonic solids are convex polyhedrons. A polyhedron is convex if for every pair of points that belong to the shape, the shape contains the whole straight line segment connecting the two points.
It is fascinating that today some astrophysicists have suggested that our entire universe may be in the form of a dodecahedron in a "wrap-around" universe whose dodecahedral faces interconnect in mysterious ways.
Atiyah, Michael and Paul Sutcliffe, "Polyhedra in Physics,
Chemistry and Geometry,"
Coxeter, H. S. M., Regular Polytopes, 3rd ed. (New York: Dover Publications, 1973).
Merali, Zeeya, "Our Finite, Wrap-Around Universe," New Scientist 197(2638): 13 (January, 2008).
Weyl, Hermann, Symmetry (Princeton, New Jersey: Princeton University Press, 1952).
 Aristotle's Organon (c. 350 BC)
Aristotle's Organon (c. 350 BC)
Aristotle, The Basic Works of
Aristotle (Modern Library Classics), Richard McKeon, ed. (
"SparkNotes: Aristotle: Organon (Aristotle's Logical Treatises): The Syllogism"; see http://www.sparknotes.com/philosophy/aristotle/section1.html.
 Aristotle's Wheel Paradox (c. 320 BC)
Aristotle's Wheel Paradox (c. 320 BC)
Ballew, David, "The Wheel of Aristotle," Mathematics Teacher, 65(6): 507-509 (1972).
Boyer, Carl B. and Uta C. Merzbach, A History of Mathematics (Hoboken, New Jersey: John Wiley & Sons, 1991).
Heath, Thomas L., The Thirteen Books of the Elements, 2nd ed. (3 volumes) (New York: Dover, 1956.) (Heath is the translator and provides an introduction and commentary.)
Archimedes: Sand, Cattle & Stomachion (c. 250 BC)
♪ Dorrie cites four scholars who do not believe that the version of the Cattle Problem that yields this huge solution is due to Archimedes, but he also cites four authors who believe that the problem should be attributed to Archimedes.
Dorrie, Heinrich, 100 Great Problems of Elementary Mathematics: Their History and Solution (New York, Dover, 1965).
Kolta, Gina "In
Archimedes' Puzzle, a New
Williams, Hugh C., German, R. A., and Zarnke, C. R., "Solution of the Cattle Problem of Archimedes," Math. Comput., 19: 671-674 (1965).
π (c. 250 BC)
♪ A New Introduction to Mathematics (1706) by Welsh mathematician William Jones (1675– 1749) is the first text in which the Greek letter π was used for this famous constant. The symbol π later became popular after Leonhard Euler started to use it in 1737.
Beckmann, Peter. A History of Pi, 3rd edition (New York: Dorset Press, 1989).
Pickover, Clifford, A Passion
for Mathematics (
Sieve of Eratosthenes (c. 240 BC)
Conway, John and Richard Guy, The Book of Numbers (New York: Copernicus/Springer, 1996).
Crandall, Richard and Carl
Pomerance, Prime Numbers: A Computational Perspective (
Archimedean Semi-Regular Polyhedra (c. 240 BC)
♪ Semi-regular polyhedra include the 13 Archimedean solids, as well as prisms and antiprisms, if all of their faces are regular polygons. (An example of a prism is a 6-sided column; that is, a standard column with a hexagonal top and bottom and 6 parallelogram faces joining corresponding sides.)
Coxeter, H. S. M., Regular Polytopes, 3rd ed. (New York: Dover Publications, 1973).
Gullberg, Jan, Mathematics: From the Birth of Numbers (New York: W. W. Norton, 1997).
Archimedes' Spiral (225 BC)
Gardner, Martin, The Unexpected Hanging and Other Mathematical Diversions. (Chicago: Chicago University Press, 1991).
Pickover, Clifford, "Mathematics and Beauty: A Sampling of Spirals and ‘Strange' Spirals in Science, Nature and Art," Leonardo, 21(2): 173-181 (1988).
Pickover, Clifford, Computers,
Pattern, Chaos, and Beauty (
Cissoid of Diocles (c. 180 BC)
Lockwood, Edward Harrington, A Book of Curves. (Cambridge, England: Cambridge University Press, 1967).
Ptolemy's Almagest (c. 150)
Gullberg, Jan, Mathematics: From the Birth of Numbers (New York: W. W. Norton, 1997)
Ptolemy, Ptolem's Almagest, translated and annotated by G. J. Toomer (Princeton, New Jersey: Princeton University Press, 1998).
Grasshoff, Gerd, The History of Ptolemy's Star Catalogue (New York: Springer, 1990).
Diophantus's Arithmetica (250)
♪ Howard Eves writes in An Introduction to the
History of Mathematics: "How and when the new numeral symbols first entered
Boyer, Carl B. and Uta C. Merzbach, A History of Mathematics (Hoboken, New Jersey: John Wiley & Sons, 1991).
Eves, Howard, An Introduction to the History of Mathematics, 6th Edition (Boston, Massachusetts: Brooks Cole, 1990).
Swift,
J. D. "Diophantus of
Pappus's Hexagon Theorem (c. 340)
Dehn, Max, "Mathematics, 600 B.C. – 600 A.D," American Mathematical Monthly, 50: 357-350 (1943).
Gardner, Martin, Mathematical Carnival (New York: Vintage, 1977).
Heath, Thomas, A History of Greek Mathematics, Volume 2 (Oxford: Clarendon Press, 1921).
Bakhshali Manuscript (c. 350)
♪ When considering the problem relating to men, women, and children, note that the problem makes use of a classic Diophantine system of equations, because an infinite number of answer sets exist if we are allowed to use fractional answers. However, the problem is solvable because we are restricted to whole numbers of people.
The date of the manuscript is still debated. Many of the earlier scholars have dated it to around 400 AD; however, Georges Ifrah writes that "the Bakhshali Manuscript cannot have been written earlier than the ninth century [however] it seems likely that the manuscript in present-day form constitutes the commentary or the copy of an anterior mathematical work."
Channabasappa, M. N., "On the Square Root Formula in the Bakhshali Manuscript," Indian J. History Sci., 11(2): 112-124 (1976).
Gupta, R. C., "Centenary of Bakhshali Manuscript's Discovery," Ganita Bharati, 3(3-4): 103-105 (1981).
Ifrah, Georges, The Universal History of Numbers (Hoboken, New Jersey: John Wiley & Sons, 1999).
Teresi, Dick, Lost Discoveries: The
Ancient Roots of Modern Science (
The Death of Hypatia (415)
Deakin, Michael A. B., Hypatia
of
Pickover, Clifford, A Passion
for Mathematics (
Zero (c. 650)
Arsham, Hossein, "Zero in Four Dimensions: Historical, Psychological, Cultural, and Logical Perspectives," The Pantaneto Forum, 2(5) (2002); see http://pantaneto.co.uk.
Seife, Charles, Zero: The
Biography of a Dangerous Idea (
Alcuin's Propositiones ad Acuendos Juvenes (c. 800 AD)
Atkinson, Leigh, "When the Pope was a Mathematician," College Mathematics Journal 36:354-362 (November, 2005).
Peterson, Ivars, "Problems to Sharpen the Young," Sciences News (online), 168(21), November 2005; see http://www.sciencenews.org/articles/20051119/mathtrek.asp.
al-Khwarizmi's Algebra (830)
Lindberg, David C., Science in the Middle Ages (Chicago: University of Chicago Press, 1980).
Rashed, Roshdi, The Development of Arabic Mathematics: Between Arithmetic and Algebra (New York: Springer, 1994).
Borromean Rings (834)
Cromwell, Peter, "The Borromean Rings"; see http://www.liv.ac.uk/~spmr02/rings/.
Cromwell, Peter,
Freedman, Michael and Richard Skora, "Strange actions of groups on spheres," Journal of Differential Geometry, 25(1): 75-98 (1987).
Lindstrom, Bernt and Hans-Olov Zetterstrom, "Borromean Circles are Impossible," The American Mathematical Monthly, 98(4): 340-341 (1991).
Tait, Peter G., "On Knots," Trans. Royal Soc. Edinburgh, 28: 145-190 (1876).
Ganita Sara Samgraha (850)
Joseph, George Gheverghese, The Crest of the Peacock: Non-European Roots of Mathematics (London: Penguin Books, 1994).
Sen, S. N., "Mathematics," In A Concise History of Science in India, edited by D. M. Bose, S. N. Sen and B.V. Subbarayappa (New Delhi: Indian National Science Academy, 1971).
Thabit Formula for Amicable Numbers (c. 850)
Abattouy, Mohammed, "Greek Mechanics in Arabic Context: Thabit ibn Qurra, al-Isfizarı and the Arabic Traditions of Aristotelian and Euclidean Mechanics," Science in Context, 14: 179-247 (2001).
Gardner, Martin, Mathematical Magic Show (Washington, DC: Mathematical Association of America, 1989).
Sayili, Aydin, "Thabit ibn Qurra's
Generalization of the Pythagorean Theorem,"
Kitab al-fusul fi al-hisab al-Hindi (c. 953)
Regis Morelon (editor), Encyclopedia of the History of Arabic Science (London: Routledge, 1996).
Saidan, A. S., "The Earliest
Extant Arabic Arithmetic: Kitab al-Fusul fi al Hisab al-Hindi of Abu al-Hasan,
Ahmad ibn Ibrahim al-Uqlidisi,"
Saidan, A. S. (translator), The
Arithmetic of Al-Uqlidisi: The Story of Hindu-Arabic Arithmetic as Told in ‘Kitab
al-Fusul fi al-Hisab al-Hindi,'
Teresi, Dick, Lost Discoveries:
The Ancient Roots of Modern Science (
Omar Khayyam's Treatise (1070)
♪ Other individuals also worked on the binomial theorem, including Chinese mathematician Yang Hui (c. 1238–1298), Indian mathematician Pingala, who appears to have lived sometime during the 3rd century BC, and Isaac Newton who generalized the formula to other exponents.
Dorrie, Heinrich, 100 Great Problems of Elementary Mathematics: Their History and Solution (New York: Dover, 1965).
Eves, Howard. "Omar Khayyam's Solution of Cubic Equations," Mathematics Teacher 51: 285-286 (1958).
Al-Samawal's The Dazzling (c. 1150)
O'Connor, John J., and Robertson, Edmund F., "Ibn Yahya al-Maghribi Al-Samawal," at "The MacTutor History of Mathematics Archive"; see http://www-gap.dcs.st-and.ac.uk/~history/Biographies/Al-Samawal.html.
Perlmann, Moshe (translator and editor), "Samau'al al-Maghribi, Ifham al-Yahud – Silencing the Jews," Proceedings of the American Academy for Jewish Research, 32: 15-25, 33-62 (1964).
Abacus (c. 1200)
♪ The word "abacus" may come from the Greek "abax" (calculating table) and/or from "abaq," the Hebrew word for dust, given that early mathematical problems were often contemplated while writing in sand or dust.
Ewalt, David, "The 20 Most Important Tools: No. 2, The Abacus"; see http://www.forbes.com/personaltech/2005/08/30/technology-calculator s-abacus_cx_de_0830abacus.html/.
Ifrah, Georges, The Universal
History of Computing: From the Abacus to the Quantum Computer (
Fibonacci's Liber Abaci (1202)
♪ Today, many authors begin the Fibonacci sequence with a 0, as in 0, 1, 1, 2, 3, 5, 8…. Interestingly, Mario Livio notes, "Each mammalian microtubule is typically made up of thirteen columns, arranged in five right-handed and eight left-handed structures (5, 8, and 13 are all Fibonacci numbers). Furthermore, occasionally one finds double microtubules with an outer envelope made up--you guessed it--of 21 columns, the next Fibonacci number."
Boyer, Carl B. and Uta C. Merzbach, A History of Mathematics (Hoboken, New Jersey: John Wiley & Sons, 1991).
Livio, Mario, "The Golden Number: Nature Seems to Have a Sense of Proportion," Natural History, 112(2): 64-69 (March, 2003).
Sigler, Laurence E. (translator), Fibonacci's Liber Abaci (
Wheat on a Chessboard (1256)
♪ A geometric sequence is a sequence of numbers in which each term after the first term is determined by multiplying the previous one by a fixed non-zero number.
Gullberg, Jan, Mathematics: From the Birth of Numbers (New York: W. W. Norton, 1997).
Wells, David, Book of Curious
and Interesting Puzzles (
Harmonic Series Diverges (c. 1350)
Dunham, William,
"The Bernoullis and the Harmonic Series," College Mathematics Journal,
Pickover, Clifford, Keys to Infinity (Hoboken, New Jersey: John Wiley & Sons, 1995).
Law of Cosines (c. 1427)
Huettenmueller, Rhonda, Pre-Calculus
Demystified (
Weisstein, Eric W. CRC Concise
Encyclopedia of Mathematics (
Peterson, Ivars, "Old and New Arithmetic," The Mathematical
Association of
Smith, David Eugene, "The First Printed Arithmetic (
Swetz, Frank, Capitalism and
Arithmetic: The New Math of the 15th Century, Including the Full Text of the
Swetz, Frank, "Fifteenth and Sixteenth Century Arithmetic Texts: What Can We Learn From Them?" Science & Education, 1(4): 365-378 (December, 1992).
Discovery of Series Formula for π (c. 1500)
♪ Ranjan Roy says that although the series formula appears in Tantrasangraha, "it is not completely clear who the discoverer of these series was. In the Aryabhatiyabhasya, a work on astronomy, Nilakantha attributes the series for sine to mathematician Madhava (1340-1425). It is not known whether Madhava found the other series as well…."
Beckmann, Peter. A History of Pi, 3rd edition (New York: Dorset Press, 1989).
Roy, Ranjan, "The discovery of the series formula for π by Leibniz, Gregory, and Nilakantha," Mathematics Magazine, 63: 291-306, 1990.
Golden Ratio (1509)
♪ The origin of the term "golden ratio" is disputed but appears to emerge in the twelfth century. Although the recent history of the golden ratio was triggered by Luca Pacioli's Divina Proportione (1509), ancient Greek mathematicians studied the ratio much earlier because it frequently appeared in geometrical studies. Mario Livio writes, "Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties."
Technically speaking, the artistic figure depicts a Fibonacci spiral, based on consecutive terms of a Fibonacci sequence. Because the ratios of consecutive terms in the Fibonacci series approach v, the two spirals are quite similar in appearance.
Livio, Mario, The Golden
Ratio (
Pickover, Clifford, A Passion
for Mathematics (
Polygraphiae Libri Sex (1518)
Kahn, David, The Codebreakers (New York: Scribner, 1996).
Peterson, Ivars, "Cracking a Medieval Code," Sciences News Online, 1998; see http://www.sciencenews.org/pages/sn_arc98/5_2_98/mathland.htm.
Loxodrome (1537)
Alexander, James,
"Loxodromes:
Gullberg, Jan, Mathematics: From the Birth of Numbers (New York: W. W. Norton, 1997).
Nunes, Pedro, Opera,
Cardano's Ars Magna (1545)
Dunham, William, Journey through Genius: The Great Theorems of Mathematics (New York: Penguin, 1991).
Gullberg, Jan, Mathematics: From the Birth of Numbers (New York: W. W. Norton, 1997).
O'Connor, John J., and Robertson, Edmund F., "Gerolamo Cardano," at "The MacTutor History of Mathematics Archive"; see http://www-history.mcs.st-andrews.ac.uk/Biographies/Cardan.html.
Sumario Compendioso (1556)
Smith, David Eugene (Introduction and translator) The Sumario Compendioso of Brother Juan Díez (Boston: Ginn and Company, 1921).
Smith, David Eugene, "The First
Work on Mathematics Printed in the
Gray, Shirley and C. Edward Sandifer, "The Sumario Compendioso: The New World's First Mathematics Book," Mathematics Teacher, 94 (2): 98 – 103 (February, 2001).
Mercator Projection (1569)
♪
Which body of land is largest: Greenland, South America, or
Short, John Rennie, The World Through Maps: A History of
Cartography (
Thrower, Norman Joseph William, Maps and Civilization: Cartography in Culture and Society, Second Edition (Chicago: University of Chicago Press, 1999).
Imaginary Numbers (1572)
Nahin, Paul, An Imaginary Tale (Princeton, New Jersey: Princeton University Press, 1998).
Kepler Conjecture (1611)
♪ In 2004, researchers reported in Science magazine that a maximally random packed state of M&Ms chocolate candies has a packing density of about 68%, or 4% greater than spheres. Using computer simulations, the researchers also showed that other ellipsoid packings result in random packing densities approaching that of the densest sphere packings (nearly filling 74% of the space).
In the 1950s, Hungarian mathematician Laszlo Fejes-Toth, showed that the most efficient stacking arrangement of spheres could be determined by examining a finite cluster of spheres. Specifically, he showed that a proof could be completed after analyzing only 50 spheres.
Donev, Aleksandar, Ibrahim Cisse, David Sachs, Evan A. Variano, Frank H. Stillinger, Robert Connelly, Salvatore Torquato, and P. M. Chaikin, "Improving the Density of Jammed Disordered Packings using Ellipsoids." Science, 303(5660): 990-993 (2004).
Hales, Thomas C. "A Proof of the Kepler Conjecture," Annals of Mathematics, 162(3): 1065-1185 (2005).
Szpiro, George G. (2003) Kepler's
Conjecture (
Logarithms (1614)
♪ Mathematician Pierre-Simon Laplace (1749–1827) noted that the inventions of logarithms "by shortening the labors doubled the life of the astronomer."
Tallack, Peter The Science Book (
Gibson, George A., "Napier and the Invention of Logarithms,"
in Handbook of the Napier Tercentenary Celebration, or Modern Instruments
and Methods of Calculation, E. M. Horsburgh (editor) (1914; reprinted in
Slide Rule (1621)
♪ Florian Cajori writes in William Oughtred (1916) that "it is by no means clear that Delamain [the student] stole the invention from Oughtred; Delamain was probably an independent inventor."
Robert Heinlein wrote in Have Spaceship–Will Travel (1958), "Dad says that anyone who can't use a slide rule is a cultural illiterate and should not be allowed to vote."
Cajori, Florian, William Oughtred: A Great Seventeenth-Century Teacher of Mathematics (Chicago: Open Court Publishing, 1916).
"The Oughtred Society Slide Rule Homepage"; see http://oughtred.org.
Stoll, Cliff, "When Slide Rules Ruled," Scientific American, 294(5): 81-84 (May 2006).
Fermat's Spiral (1636)
Krawczyk, Robert J., "Fermat's
Spiral Mandalas," Bridges 2005 Conference: Mathematical Connections
in Art, Music, and Science,
Krizek, Michal, Florian Luca, and
Mahoney, Michael Sean, The Mathematical Career of Pierre de Fermat, 1601-1665 (Princeton, New Jersey: Princeton University Press, 1994).
Naylor, Michael. "Golden, sqrt(2), and π Flowers: A Spiral Story," Mathematics Magazine 75(3): 163-172 (June, 2002).
Fermat's Last Theorem (1637)
Aczel, Amir, Fermat's Last Theorem: Unlocking the Secret of an Ancient Mathematical Problem (New York: Delta, 1997).
Singh, Simon, Fermat's Last
Theorem (
Descartes' La Geometrie (1637)
Boyer, Carl B. and Uta C. Merzbach, A History of Mathematics (Hoboken, New Jersey: John Wiley & Sons, 1991).
Gardner, Martin, Mathematical Carnival (New York: Vintage, 1977).
Grabiner, Judith, "Descartes and Problem-Solving," Mathematics Magazine 68(2): 83-97 (1995).
Gullberg, Jan, Mathematics: From the Birth of Numbers (New York: W. W. Norton, 1997).
Cardioid (1637)
Castillon, Johann, "De curva cardiode," Philosophical Transactions of
the Royal Society. 41: 778-781 (1741). (While in
Vecchione, Glen, Blue Ribbon Science Fair Projects (
Logarithmic Spiral (1638)
Gardner, Martin, The Unexpected Hanging and Other Mathematical Diversions. (Chicago: Chicago University Press, 1991).
Hargittai, Istvan and Clifford A. Pickover (editors) Spiral Symmetry (River Edge, New Jersey: World Scientific, 1992).
Pickover, Clifford, "Mathematics and Beauty: A Sampling of Spirals and ‘Strange' Spirals in Science, Nature and Art," Leonardo, 21(2): 173-181 (1988).
Pickover, Clifford, Computers,
Pattern, Chaos, and Beauty (
Projective Geometry (1639)
♪ William P. Berlinghoff and Fernando Q. Gouvêa write, "Among the most prominent people of the 15th and early 16th centuries who studied, used, and advanced this mathematical theory of perspective were Italian artists Piero della Francesca (c. 1410-1492) and Leonardo da Vinci (1452-1519), and also German artist Albrecht Dürer (1471-1528), who wrote a widely used book on the subject."
Berlinghoff, William P. and
Fernando Q. Gouvêa, Math Through the Ages: A Gentle History for Teachers and
Others, Expanded Edition (
Coxeter, Harold Scott McDonald, Projective Geometry, 2nd Edition (New York: Springer, 1987).
Field, Judith Veronica, Piero
Della Francesca: A Mathematician's Art (
Veblen, Oswald and John W. Young, Projective Geometry, 2 volumes. (Boston: Ginn, 1938).
Torricelli's Trumpet (1641)
♪ According to Julian Fleron, Torricelli's Trumpet "propelled Torricelli into the mathematical spotlight, gave rise to many related paradoxes, and sparked an extensive philosophical controversy that included Thomas Hobbes, John Locke, Isaac Barrow and others."
dePillis, John, 777
Mathematical Conversation Starters. (
Fleron, Julian, "Gabriel's Wedding Cake, The College Mathematics Journal,
30(1): 35-38 (January, 1999).
Mancosu, Paolo and Ezio Vailati,
"Torricelli's Infinitely Long Solid and Its Philosophical Reception in the
Seventeenth Century,"
Pickover, Clifford, A Passion
for Mathematics (
Pascal's Triangle (1654)
Gordon, James, A. Goldman, J. Maps, D. Costello, R. Tiberio, and B. Whitehead, "Superconducting-Normal Phase Boundary of a Fractal Network in a Magnetic Field," Physical Review Letters 56(21): 2280-2283 (1986).
Gardner, Martin, Mathematical Carnival (New York: Vintage Books, 1977).
Pickover, Clifford, "On the Aesthetics of Sierpinski Gaskets Formed from Large Pascal's Triangles," Leonardo, 23(4): 411-417 (1990).
The Length of Neile's Semicubical Parabola (1657)
Wallis, John (translated and
introduced by Jacqueline A. Stedall), The Arithmetic of Infinitesimals: John
Wallis 1656 (
Viviani's Theorem (1659)
De Villiers, Michael "Crocodiles and Polygons," Mathematics in School, 34(2): 2-4 (March 2005); see http://mysite.mweb.co.za/residents/profmd/vivianigen.pdf.
De Villiers, Michael, Rethinking Proof with Sketchpad (
Natucci, A., "Vincenzo Viviani," in Dictionary of Scientific Biography, Gillispie, Charles, Editor-in-Chief (New York: Charles Scribner's Sons, 1970).
Viviani, Vincentio, De
maximis, et minimis geometrica divinatio in quintam Conicorum Apollonii Pergaei
ad hunc desideratum; liber primus (et secundus) (
Discovery of Calculus (c. 1665)
♪ In 1671,
Pickover, Clifford, Calculus
and Pizza (
Bardi, Jason Socrates, The Calculus
Wars:
Kleiner, Israel, "History of the Infinitely Small and the Infinitely Large in Calculus," Journal Educational Studies in Mathematics, 48(2-3); 137-174 (November, 2001).
Kelley, Carl T., Solving Nonlinear
Equations with Newton's Method (
Hamming, Richard Wesley, Numerical Methods for Scientists and Engineers (New York: Dover, 1986).
Tautochrone Problem (1673)
Darling, David, The Universal Book of Mathematics (
Gardner, Martin, The Sixth Book of Mathematical Games from Scientific American (Chicago: University of Chicago Press, 1984).
Astroid (1674)
McCreary, Charles H., US Patent
No. 4,987,984: "
L'Hopital's Analysis of the Infinitely Small (1696)
Ball, W. W. Rouse, A Short Account of the History of Mathematics, Fourth Edition (New York: Dover, 1960), reprint of 1908 edition.
Devlin, Keith, "Spreading the Word," November, 1996, The Mathematical Association of America; see http://www.maa.org/devlin/devlin_nov96.html.
Kleiner, Israel, "History of the Infinitely Small and the Infinitely Large in Calculus," Journal Educational Studies in Mathematics, 48(2-3); 137-174 (November, 2001).
Rope around the Earth Puzzle (1702)
Darling, David, The Universal Book of Mathematics (
Force, James E., William Whiston:
Honest Newtonian (
Law of Large Numbers (1713)
Grinstead, Charles M. and James Laurie Snell, Introduction to Probability (Providence, Rhode Island: American Mathematical Society, 1997).
Shafer, Glenn, "The significance of Jacob Bernoulli's Ars Conjectandi for the philosophy of probability today," Journal of Econometrics, 71(1): 15-32 (1996).
Euler's Number, e (1727)
♪ The mathematical constant e is special for numerous reasons. For example, f(x) = ex is its own derivative (i.e., the slope of the tangent line at any point along the curve represented by ex is ex). Additionally, the area under the graph y = 1/x over the interval 1 ≤ x ≤ e is exactly equal to 1. In other words, the area between the curve y = 1/x and the x-axis is 1 over this interval.
Darling, David,
The Universal Book of Mathematics (
Kasner, Edward and James Newman, Mathematics and the
Imagination (
Maor, Eli, e: The Story of a Number (Princeton, New Jersey: Princeton University Press, 1998).
♪
The formula n! ≈
ce-nnn+1/2 was first discovered by Abraham de Moivre (1667-1754), where c
is a constant.
Ball, Keith M., Strange Curves,
Counting Rabbits, and Other Mathematical Explorations (
Hubbard, John
Rast, Schaum's Outline of Theory and Problems of Data Structures with Java
(
Stirling, James, Methodus Differentialis sive
Tractatus de Summatione et Interpolatione Serium Infinitarum (
Normal Distribution Curve (1733)
♪ Abraham de Moivre is also famous for de Moivre's formula, which links trigonometry and complex numbers.
Patel, Jagdish K.,
Galton, Francis, Natural Inheritance (London: Macmillan, 1889).
Euler–Mascheroni Constant (1735)
Havil,
Julian, Gamma, Exploring Euler's Constant (
Conway, John and Richard Guy, The Book of Numbers (New York: Copernicus/Springer, 1996).
Konigsberg Bridges (1736)
Euler, Leonhard, "Solutio problematis ad geometriam situs pertinentis." Comment. Acad. Sci. U. Petrop. 8: 128-140 (1736). Reprinted in Opera Omnia Series Prima, Volume 7, pp. 1-10 (1766).
Newman,
James, "Leonhard Euler and the
Martin, Robert, "The St. Petersburg Paradox," Stanford Encyclopedia of Philosophy; see http://plato.stanford.edu/entries/paradox-stpetersburg/.
Bernstein, Peter L., Against the Gods: The Remarkable Story of Risk (Hoboken, New Jersey: John Wiley and Sons, 1998).
Goldbach Conjecture (1742)
Doxiadis, Apostolos, Uncle
Petros and Goldbach's Conjecture (
Wang, Yuan, Goldbach
Conjecture, Second Edition (River Edge,
Agnesi's Instituzioni Analitiche (1748)
♪ Italian scientist Laura Bassi (1711–1778) is usually considered to be the first woman faculty member at a recognized university.
Mazzotti,
Massimo, The World of Maria Gaetana Agnesi, Mathematician of God (
O'Connor, John J,
and Robertson, Edmund F., "Maria Gaëtana Agnesi" at "The MacTutor History of
Mathematics Archive,"
Truesdell, Clifford, "Maria Gaetana Agnesi," Archive for History of Exact Science 40: 113-142 (1989).
Struik, Dirk (editor), A Source Book in Mathematics, 1200-1800 (Princeton, New Jersey: Princeton University Press, 1986).
Euler's Formula for Polyhedra (1751)
Darling, David, The Universal Book of Mathematics (
Euler, Leonhard, "Elementa doctrinae solidorum," Novi commentarii academiae scientiarum Petropolitanae 4: 109-140 (1752), reprinted in Opera Omnia Series I, Volume 26, pp. 71-93.
Wells, David, "Are these the most beautiful?" Mathematical Intelligencer, 12(3):3 7-41 (1990).
Wells, David, "Which is the most beautiful?" Mathematical Intelligencer, 10(4): 30-31 (1988).
Euler's Polygon Division Problem (1751)
Dorrie, Heinrich, 100 Great Problems of Elementary Mathematics: Their History and Solution (New York: Dover, 1965).
Forder, H. G., "Some Problems in Combinatorics," The Mathematical Gazette, 45(353): 199-201 (October, 1961).
Knight's
Dudeney, Henry E., Amusements in Mathematics (New York: Dover, 1970), first published in 1917.
Euler, Leonhard. "Solution d'une question curieuse qui ne paroit soumise a aucune analyse," Memoires de l'Academie Royale des Sciences et Belles Lettres de Berlin, Annee 1759, 15: 310-337 (1766).
Pickover, Clifford, The Zen
of Magic Squares, Circles, and Stars (
Stewart, Ian, Another Fine Math You've Got Me Into (New York: Freeman, 1992).
Watkins, John, Across the
Board: The Mathematics of Chessboard Problems (
Bayes' Theorem (1761)
♪ Some historians feel that English mathematician Nicholas Saunderson (1682–1739) may have discovered Bayes' theorem before Bayes.
Bayes, Thomas, "An Essay towards solving a Problem in the Doctrine of Chances. By the late Rev. Mr. Bayes, F. R. S. communicated by Mr. Price, in a letter to John Canton, A. M. F. R. S.," Philosophical Transactions, 53: 370–418 (1763).
Stigler, Stephen M., "Thomas Bayes' Bayesian Inference," Journal of the Royal Statistical Society, Series A, 145: 250–258 (1982).
Ahmed, Maya. M. "How Many Squares are
There, Mr. Franklin? Constructing and Enumerating
Pickover, Clifford, The Zen
of Magic Squares, Circles, and Stars (
Patel, Lalbhai, "The Secret of Franklin's 8×8 ‘Magic' Square," The Journal of Recreational Mathematics, 23(3): 175-182 (1991).
Minimal Surface (1774)
Darling, David, The Universal Book of Mathematics (
Hoffman, David, "The Computer-Aided Discovery of New Embedded Minimal Surfaces," Mathematical Intelligencer, 9(3): 8-21 (1987).
Buffon's Needle (1777)
♪ Research suggests that a certain ant species uses the equivalent of a Buffon's needle algorithm to measure the size of potential nest sites.
Mathematically, it can be shown that with an infinite number of toothpick drops, the probability actually equals pi.
Buffon, Georges-Louis, "Essai d'arithmetique morale," Histoire naturelle, generale er particulière, Supplement 4 : 46-123 (1777).
Mallon, Eamonn B., and Nigel R. Franks, "Ants estimate area
using Buffon's Needle," Proceedings of the Royal Society,
Thirty-Six Officers Problem (1779)
Bose, Raj C., Shrikhande, S. S., and Parker, E. T., "Further Results on the Construction of Mutually Orthogonal Latin Squares and the Falsity of Euler's Conjecture," Canad. J. Math., 12: 189-203 (1960).
Tarry, Gaston. "Le problème de 36 officiers," Compte Rendu de l'Assoc. Français Avanc. Sci. Naturel, 1: 122-123 (1900).
Pickover, Clifford, The Zen
of Magic Squares, Circles, and Stars (
Huczynska, Sophie, "Powerline communication and the 36 Officers Problem," Philosophical Transactions of the Royal Society (A Mathematical, Physical, and Engineering Sciences), 364(1849): 3199-214 (December 2006).
Sangaku Geometry (c. 1789)
Bogomolny, Alexander, "Sangaku: Reflections on the Phenomenon"; see http://www.cut-the-knot.org/pythagoras/Sangaku.shtml.
Rothman, Tony and
Fukagawa, Hidetoshi, "Japanese
Least Squares (1795)
♪ The full title of Gauss's Heavenly Bodies work is below.
Gauss, Carl Friedrich Theoria motus corporum coelestium in sectionibus conicis solem ambientium (Theory of the Motion of the Heavenly Bodies Moving about the Sun in Conic Sections) (Hamburg: F. Perthes and I. H. Besser, 1809).
Gauss, Carl Friedrich, "Theoria combinationis obsevationum erroribus minimis obnoxiae," Werke, Volume 4. (Gottingen, Germany, 1823).
Constructing a Regular Heptadecagon (1796)

Bühler, Walter K., Gauss, A Biographical Study (
Dunnington, G. Waldo, "The Sesquicentennial of the Birth of Gauss," The Scientific Monthly, 24: 402-414, May, 1927; see http://www.mathsong.com/cfgauss/Dunnington/1927/.
du Sautoy, Marcus, The Music of the
Primes: Searching to Solve the Greatest Mystery in Mathematics (
Dunnington, G. Waldo, Gauss: Titan of Science (
Hall, Tord, Carl Friedrich Gauss (Cambridge, Massachusetts, MIT Press, 1970).
Hayes, Brian, Gauss's Day of Reckoning, 94(3): 200, May/June, 2006; see http://www.americanscientist.org/template/AssetDetail/assetid/50686.
May, Kenneth O., "Carl Gauss," in Dictionary of Scientific Biography, Gillispie, Charles, Editor-in-Chief (New York: Charles Scribner's Sons, 1970).
Pickover, From Archimedes to
Hawking: Laws of Science and the Great Minds Behind Them (
Rassias, George M. The Mathematical Heritage of C. F. Gauss (River Edge, New Jersey: World Scientific, 1991).
Tent, M. B. W., Prince of Mathematics: Carl Friedrich Gauss
(
von Waltershausen, Sartorius, Gauss zum Gedächtniss (Leipzig, 1856).
Fundamental Theorem of Algebra (1797)
Dunham, William, "Euler and the Fundamental Theorem of Algebra," College Mathematics Journal, 22: 282-293 (1991).
Fine, Benjamin and Gerhard Rosenberger, The Fundamental Theorem of Algebra (New York: Springer, 1997).
Gauss's Disquisitiones Arithmeticae (1801)
Gauss, Carl F., Disquisitiones Arithmeticae, Arthur A. Clarke (translator) (New York Springer, 1986), 2nd printing edition. Translation of 1801 Latin edition.
Hawking, Stephen, God Created
the Integers (
Three-Armed Protractor (1801)
United States Hydrographic Office,
Bay of Bengal Pilot: Bay of Bengal and the Coasts of
Huddart, William, Unpathed Waters: Account of the Life and Times of Captain Joseph Huddart F.R.S. (London: Quiller Press, 1989).
Fourier Series (1807)
Fourier, Joseph,
The Analytical Theory of Heat (
Jeans, James Hopwood, Science and Music (New York: Dover, 1968).
Ravetz, Jerome and I. Grattan-Guiness, "Fourier," in Dictionary of Scientific Biography, Gillispie, Charles, Editor-in-Chief (New York: Charles Scribner's Sons, 1970).
Laplace's Theorie Analytique des Probabilites (1812)
Hawking, Stephen, God Created
the Integers (
Laplace, Marquis de, Introduction
to the Analytical Theory of Probability (
Richeson, A. W., "
♪ Although John Wallis was the first to write on this problem, I date the entry according to Pieter Nieuwland's actual finding of the maximal cube that will pass through a cube. Some sources appear to suggest that Wallis's writing on the problem did not appear until the second edition of his book, published in 1693.
Guy, Richard K., and Richard J. Nowakowski, "Monthly Unsolved Problems, 1969-1997," The American Mathematical Monthly, 104(10): 967-973 (December 1997).
Schrek, D. J. E., "
van Swinden, Jan Hendrik, Grondbeginsels der Meetkunde (Amsterdam, 1816). (This is the second edition of van Swinden book on geometry.)
Wallis, John, De Algebra Tractatus
(Second Edition) (
Bessel Functions (1817)
Bowman, Frank, Introduction to Bessel Functions (Dover: New York, 1958).
Korenev, Boris Grigor'evich, Bessel
Functions and Their Applications (
Babbage Mechanical Computer (1822)
Norman, Jeremy, From
Gutenberg to the Internet: A Sourcebook on the History of Information Technology
(
Swade, Doron, "Redeeming Charles Babbage's Mechanical Computer," Scientific American, 268(2): 86-91 (February, 1993).
Cauchy's Le Calcul Infinitesimal (1823)
Grabiner, Judith, The Origins of Cauchy's Rigorous Calculus (Cambridge: MIT Press, 1981).
Hawking, Stephen, God Created
the Integers (
Waterhouse, William, "Book Review of The origins of Cauchy's Rigorous Calculus," Bulletin of the American Mathematical Society, 7(3): 634-638 (1982).
Barycentric Calculus (1827)
Gray, Jeremy, "Mobius's
Geometrical Mechanics," in Fauvel, J., R. Flood, and R. Wilson, eds. Mobius and His Band: Mathematics and
Astronomy in Nineteenth-Century
Pickover, Clifford, The
Mobius Strip (
Mobius, August F., Der Barycentrische Calcul (Hildesheim, Germany: Georg Olms, 1976). Original edition, published in
Non-Euclidean Geometry (1829)
Coxeter, H. S. M., Non-Euclidean Geometry, 6th Edition (Washington DC: The Mathematical Association of America, 1998).
Gray, Jeremy J., Janos Bolyai, Non-Euclidean Geometry,
and the Nature of Space (
Tallack, Peter, The Science Book (
Mobius Function (1831)
♪ Although August Mobius worked on the sequence in 1831, Carl Friedrich Gauss did initial work on the sequence more than 30 years before Mobius.
Billingsley, Patrick, "Prime numbers and Brownian motion," American Mathematical Monthly, 80: 1099, 1973. (Addresses the use of the Mobius function in quantum field theory.)
Gauss, Carl F., Disquisitiones Arithmeticae, Arthur A. Clarke (translator) (New York Springer, 1986), 2nd printing edition. Translation of 1801 Latin edition.
Mobius, August F., "Uber eine besondere Art von Umkehrung der Reihen," J. Reine Angew. Math. 9: 105-123 (1832).
Pickover, Clifford, The Mobius
Strip (
Spector, Donald, "Supersymmetry and the Möbius Inversion Function," Communications in Mathematical Physics. 127: 239, 1990
Wolf, Marek, "Applications of Statistical Mechanics in Prime Number Theory," Physica A: Statistical Mechanics and its Applications, 274(1-2): 149-157 (1999).
Group Theory (1832)
♪ It would be incorrect to imply that all of group theory had come to Galois during his final night. Ivars Peterson writes, "In fact, Galois had been writing papers on the subject since the age of 17, and the new idea of ‘group' that he had introduced is found in all of them. Nonetheless, Galois did help create a field that would keep mathematicians busy for hundreds of years, but not in one night!"
Joyner, David, Adventures in Group
Theory: Rubik's Cube, Merlin's Machine, and Other Mathematical Toys (
Peterson, Ivars, "The Galois Story," 169(8), Science News
Online,
Pigeonhole Principle (1834)
Chen, Chuan-Chong and Khee-Meng Koh, Principles and Techniques in Combinatorics (River Edge, New Jersey: World Scientific, 1992).
Robinson, Raphael M., "On the Simultaneous Approximation of Two Real Numbers," presented to the American Mathematical Society on November 23, 1940, and published in Bulletin of the American Mathematical Society 47(6): 512-513 (1941).
Quaternions (1843)
♪ Hamilton published many papers developing the theory of quaternions, including a paper "On Quaternions, or on a New System of Imaginaries in Algebra," published in installments in the Philosophical Magazine between 1844 and 1850.
Conway, John Horton, and Smith,
Derek A., On Quaternions and Octonions: Their Geometry, Arithmetic, and
Symmetry (
Hanson, Andrew J., Visualizing Quaternions (San Fransico: Morgan Kaufmann, 2006).
Kuipers, Jack B., Quaternions and Rotation Sequences: A Primer with
Applications to Orbits, Aerospace, and Virtual Reality (
Transcendental Numbers (1844)
♪
Howard Eves writes of Charles Hermite, "Pythagoras entertained this idea of
mathematical existence, as have many mathematicians after him. Hermite was a
confirmed believer in the twilight land of mathematical existence. To him,
numbers and all their beautiful properties have always had an existence of
their own, and occasionally some mathematical
Baker, Alan, A Concise Introduction to the Theory of Numbers (Cambridge: Cambridge University Press, 1985).
Eves, Howard, An Introduction to the History of Mathematics, 6th Edition (Boston, Massachusetts: Brooks Cole, 1990).
Hilbert, David, "Über die Transcendenz der Zahlen e und π," Mathematische Annalen 43: 216–219 (1893).
Liouville, Joseph, "Nouvelle demonstration d'un theorème sur les irrationalles algebriques, insere dans le Compte rendu de la dernière seance," C. R. Acad. Sci. Paris, 18: 910-911 (1844).
Liouville, Joseph, "Sur des classes très-etendues de quantites dont la valeur n'est ni algebrique, ni même reductible à des irrationelles algebriques," J. Math. Pures Appl. 15: 133-142 (1851).
Pickover, Clifford, A Passion
for Mathematics (
Catalan Conjecture (1844)
Mihăilescu, Preda, "Primary Cyclotomic Units and a Proof of Catalan's Conjecture," J. Reine Angew. Math. 572: 167–195 (2004).
Peterson, Ivars, "Conquering
Catalan's Conjecture," Science News Online, 161(25),
Tijdeman, Robert, "On the Equation of Catalan," Acta Arithmetica, 29: 197-209 (1976).
The Matrices of Sylvester (1850)
Horn, Roger A. and Charles R. Johnson, Matrix Analysis (Cambridge: Cambridge University Press, 1990).
Sylvester, James J. "Additions to the Articles ‘On a New Class of Theorems' and ‘On Pascal's Theorem'," Philosophical. Magazine, 37: 363-370 (1850). Reprinted in The Collected Mathematical Papers of James Joseph Sylvester, Volume 1, (1837–1853) (Cambridge, England: Cambridge University Press, 1904).
Sylvester, James J., "An Essay
on Canonical Forms, Supplement to a Sketch of a Memoir on Elimination,
Transformation and Canonical Forms," (privately printed in
Four-Color Theorem (1852)
Appel, Kenneth and Wolfgang Haken, "Every Planar Map is Four Colorable," Bull. Amer. Math. Soc. 82(5): 711-712 (1976).
Appel, Kenneth and Wolfgang Haken, "Every
Planar Map is Four Colorable: Part I. Discharging,"
Appel, Kenneth, Wolfgang Haken, and J.
Koch, "Every Planar Map is Four Colorable: Part II. Reducibility,"
Mackenzie, Dana, "What in the Name of Euclid is Going on Here?" Science,
307(5714): 1402,
May, Kenneth O. "The Origin of the
Four-Color Conjecture,"
Pickover, Clifford, The Mobius Strip (
Wilson, Robin, Four Colors Suffice
(
Boolean Algebra (1854)
De Morgan, Augustus A Budget of Paradoxes (London: Longmans, Green, and Co., 1872).
MacHale, Desmond, George Boole: His Life and Work (Dublin: Boole Press, 1985).
O'Connor, John J., and Robertson, Edmund F., "George Boole," at "The MacTutor History of Mathematics Archive"; see http://www-gap.dcs.st-and.ac.uk/~history/Biographies/Boole.html.
Icosian Game (1857)
Gardner, Martin, "Mathematical
Games: About the Remarkable Similarity between the Icosian Game and the Towers
of
Rubin,
Frank, "Search Procedure for
Harmonograph (1857)
♪ Lissajous curves were actually first studied by the American mathematician Nathaniel Bowditch in 1815 and investigated independently by Jules Antoine Lissajous in 1857.
Hal Robinson, in a personal communication to me, notes that we may want to ask if Lissajous' patterns should really be considered "harmonographs," given that such early patterns may not have been recorded as persistent graphs. Note also that in actual harmonographs, the resultant attractive graphs depend on the gradual decay in the oscillations.
The first patent for innovations in harmonograph design appeared in the early 1900s. In the 1960s, Ivan Moscovich was an early pioneer in creating mechanically efficient, large harmonographs by linking pendulums to a vertical surface.
Ashton, Anthony, Harmonograph:
A Visual Guide to the Mathematics of Music (
Pickover, Clifford, The Heaven
Virus (
Wells, David, The Penguin Dictionary of Curious and Interesting Geometry, (New York: Penguin, 1992).
The Mobius Strip (1858)
Fauvel, John, Raymond Flood, and Robin Wilson, Mobius and His Band (New York: Oxford University Press, 1993).
Pickover, Clifford, The Mobius Strip (
Gardner, Martin, Hexaflexagons and Other Mathematical Diversions (Chicago, University of Chicago Press; reprint edition, 1988)
Holditch's Theorem (1858)
Bender, William, "The Holditch Curve Tracer," Mathematics Magazine, 54(3): 128-129 (1981).
Broman, Arne, "Holditch's Theorem," Mathematics Magazine, 54(3): 99-108 (May 1981).
Cooker, Mark J., "An Extension of Holditch's Theorem on the Area within a Closed Curve," The Mathematical Gazette, 82(494): 183-188 (July 1998).
Holditch, Hamnet, "Geometrical Theorem," The Quarterly Journal of Pure and Applied Mathematics, 2: 38–39 (1858).
Wells, David, The Penguin Dictionary of Curious and Interesting Geometry, (New York: Penguin, 1992).
Riemann Hypothesis (1859)
Derbyshire, John, Prime
Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics
(
Pickover, Clifford, Wonders of Numbers
(
Riemann, Bernhard, "Über die Anzahl der Primzahlen unter einer gegebenen Grosse" ("On the Number of Primes Less Than A Given Quantity"), Monatsberichte der Berliner Akademie 671-680 (November, 1859).
Beltrami's Pseudosphere (1868)
Beltrami, Eugenio, "Saggio di interpetrazione della geometria non-euclidea,"
Giornale di Matematiche, 6: 284-312 (1868).
Boyer, Carl B. and Uta C. Merzbach, A History of Mathematics (Hoboken, New Jersey: John Wiley & Sons, 1991).
Darling, David, The Universal Book of Mathematics (
Milnor, John W., "Hyperbolic Geometry: The First 150 Years," Bulletin of the American Mathematical Society, 6(1): 9-24 (1982).
Weierstrass Function (1872)
du Bois-Reymond, Paul, "Versuch einer Classification der willkürlichen Functionen reeller Argumente nach ihren Änderungen in den kleinsten Intervallen," J. Reine. Angew. Math. 79: 21-37 (1875).
Hardy, G. H., "Weierstrass's Nondifferentiable Function," Transactions of the American Mathematical Society, 17: 301-325 (1916).
Thim, Johan, "Continuous Nowhere Differentiable Functions," Masters Thesis, Department of Mathematics, Luleå University of Technology, Luleå, Sweden (2003); see http://epubl.luth.se/1402-1617/2003/320/LTU-EX-03320-SE.pdf.
Weierstrass, Karl, "Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzeren einen bestimmten Differentialquotienten besitzen," presented to the Konigl. Akad. Wiss. in 1872 but first published in Mathematische Werke von Karl Weierstrass, Band II, (Berlin: Mayer & Müller, 1985). An English translations appears in "On Continuous Functions of a Real Argument That do not have a Well-Defined Differential Quotient," Gerald A. Edgar (editor), Classics on Fractals (Boston: Addison-Wesley Publishing Company, 1993), reprinted in 2003 by Perseus Books of New York.
Gros's Theorie du Baguenodier (1872)
♪
Some time around 1500, Italian
mathematician Luca Pacioli was first to mentioned the puzzle in
Darling, David, The Universal Book of Mathematics (
Knuth, Donald, The Art of Computer Programming, Second Edition (Boston: Addison-Wesley Publishing Company, 1998).
Louis Gros, Theorie du Baguenodier (Lyon: Aime Vingtrinier, 1872), published anonymously.
The Doctorate of Kovalevskaya (1874)
Koblitz, Ann Hibner, A Convergence of Lives: Sofia Kovalevskaia: Scientist, Writer, Revolutionary (Rutgers, New Jersey: Rutgers University Press, 1993).
Kovalevskaya, Sofia, A Russian Childhood (translated by B. Stillman) (New York: Springer, 1978).
Spicci, Joan, Beyond
the Limit: The Dream of Sofya Kovalevskaya (
Fifteen Puzzle (1874)
Pickover, Clifford, The Zen
of Magic Squares, Circles, and Stars (
Slocum, Jerry and Dic Sonneveld, The 15 Puzzle: How it
Drove the World Crazy (
Yakov Perelman, Fun with Maths and Physics (Moscow: Mir Publishers, 1988).
Cantor's Transfinite Numbers (1874)
♪ Cantor's most important work relating to transfinite numbers spanned the years from about 1874 to 1883. He fully explored his thoughts on transfinite numbers in his best‑known work "Beiträge zur Begründung der transfiniten Mengelehre" ("Contributions to the founding of the theory of transfinite numbers"), Mathematische Annalen, 46: 481-512 (1895). An English translation was published in 1915. A 1955 reprint of this work is available today from Dover Publications.
Georg Cantor's first proof demonstrating that the set of all real numbers is uncountable, and that no one-to-one correspondence can exist between the real numbers and natural numbers, was formulated in 1873 and published in: Cantor, Georg, "Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen" ("On a property of the Collection of All Real Algebraic Numbers"), Journal für die Reine und Angewandte Mathematik (Journal for Pure and Applied Mathematics) 77: 258–262 (1874). Also see the following references.
Dauben, Joseph Warren, Georg Cantor: His Mathematics and Philosophy of the Infinite (Cambridge, Massachusetts: Harvard University Press, 1979).
Rucker, Rudy, Infinity and the Mind (Princeton, New Jersey: Princeton University Press, 1995).
Reuleaux Triangle (1875)
Morrell, Roger,
Jerome Gunn, and Gerald Gore, "Square Hole Drill,"
Pickover, Clifford, The Mobius Strip (
Reuleaux, Franz, The Kinematics of Machinery: Outlines of a Theory of Machines (London: Macmillan, 1876), translation of 1875 German original. Reprinted as The Kinematics of Machinery (New York: Dover, 1963.)
Harmonic Analyzer (1876)
"Harmonic analyzer,"
Henrici, Olaus, "Henrici's Harmonic Analyzer," Philosophical Magazine, 38: 110 (1894).
Montgomery, H. C., "An Optical Harmonic
Analyzer," The Journal of the Acoustical Society of
Smith, Crosbie W., Energy and Empire: A Biographical Study of Lord Kelvin (Cambridge: Cambridge University Press, 1989).
Thomson, William, "Harmonic Analyzer" (shown and explained by Sir William Thomson, F.R.S., Professor of Natural Philosophy in the University of Glasgow), Proceedings of the Royal Society of London, 27: 371-373 (1878).
Thomson, William and Tait, Peter G., Treatise on Natural Philosophy. (Oxford: Clarendon Press, 1867), published as a second edition by Cambridge University Press in 1878.
Ritty Model I Cash Register (1879)
"Inventor of the Week: James Ritty," Lemelson-MIT Program; see http://web.mit.edu/invent/iow/ritty.html.
Cortada, James W., Before the Computer: IBM, NCR, Burroughs, and Remington Rand and the Industry They Created, 1865-1956 (Princeton, New Jersey: Princeton University Press, 1993).
Venn Diagrams (1880)
Cipra, Barry, "Diagram
Masters Cry ‘Venn-i, Vidi, Vici'," Science, 299(5607): 651,
Edwards, Anthony W. F., Cogwheels of
the Mind (
Edwards, Anthony W. F., "Venn Diagrams for Many Sets," Bulletin of the
International Statistical Institute,
47th Session,
Edwards, Anthony W. F., "Venn Diagrams for Many Sets," New Scientist,
Edwards, Anthony W. F., "Rotatable Venn Diagrams," Mathematics Review,
Edwards, Anthony W. F., "Seven-set Venn Diagrams with Rotational and Polar Symmetry," Combinatorics, Probability, and Computing, 7(2): 149-152 (1998).
Grünbaum, Branko, "Venn Diagrams and Independent Families of Sets," Mathematics Magazine, 48: 12-23 (Jan-Feb 1975).
Hamburger, Peter, "Peter Hamburger's Web Site"; see http://www.ipfw.edu/math/Hamburger/.
Pickover, Clifford, A Passion
for Mathematics (
Venn, John, "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings," Philosophical Magazine and Journal of Science, Fifth Series, 9(59): 1-18 (July 1880).
Benford's Law (1881)
Benford, Frank, "The Law of Anomalous Numbers," Proceedings of the American Philosophical Society, 78 (4): 551–572 (March, 1938).
Browne, Malcolm W., "Following Benford's
Law, or Looking Out for No. 1," The
Hill, Theodore, "The First Digit Phenomenon," American Scientist, 86(4): 358-363 (1998).
Knott Ron, "The Mathematical Magic of the Fibonacci Numbers"; see http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibmaths.html#msds.
Ley, Eduardo, "On the Peculiar Distribution of the
Newcomb, Simon "Note on the frequency of Use of the Different Digits in Natural Numbers," American Journal of Mathematics, 4(1/4): 39-40 (1881).
Nigrini, Mark J., "I've Got Your Number," Journal of Accountancy Online 187(5) (May 1999); see http://www.aicpa.org/pubs/jofa/may1999/nigrini.htm. (CPAs are using Benford's Law to detect errors and irregularities in company data.)
Nigrini, Mark., "A Taxpayer Compliance Application of Benford's Law," Journal of the American Taxation Association, 18(1): 72-91 (1996).
Pickover, Clifford, A Passion
for Mathematics (
Raimi, Ralph, "The Peculiar Distribution of First Digits," Scientific American, 221: 109-119 (December 1969).
Washington, Lawrence C., "Benford's Law for Fibonacci and Lucas Numbers," The Fibonacci Quarterly, 19(2): 175-177 (1981).
Klein Bottle (1882)
Pickover, Clifford, The
Mobius Strip (
Stewart, Ian, "Glass Klein Bottles," Scientific American 278(3): 100-101 (1998).
Stoll, Cliff, "Acme Klein Bottle"; see http://www.kleinbottle.com/.
Brousseau,
Alfred, "
Gardner, Martin, "Mathematical
Games: About the Remarkable Similarity between the Icosian Game and the Towers
of
Poole, David G., "The
Towers and Triangles of Professor Claus (or, Pascal Knows
Flatland (1884)
Flatland: A Romance of Many Dimensions (Princeton, New Jersey: Princeton University Press, 1991). (This edition of the 1884 novella has an introduction written by Tom Banchoff.)
Abbott, Edwin A. and Ian Stewart, The Annotated Flatland:
A Romance of Many Dimensions (
Pickover, Clifford, Surfing through Hyperspace (New York: Oxford University, Press, 1999).
Tesseract (1888)
Banchoff, Thomas, Beyond the Third
Dimension: Geometry, Computer Graphics,
and Higher Dimensions, Second Edition (
Ehrenfest, Paul, "In What Way Does It
Become Manifest in the Fundamental Laws of Physics that Space Has Three
Dimensions?" Proceedings of the
Freeman, Ira, "Why is Space Three-Dimensional?" American Journal of Physics, 37(12): 1222-1224 (1969), adapted from W. Büchel, "Warum hat der Raum drei Dimensionen? " Physikalische Blätter, 12: 547-549 (December, 1963).
Gardner, Martin, The Unexpected Hanging (New York: Simon & Schuster, 1969).
Heinlein, Robert, "--And he Built a Crooked House," in Fantasia Mathematica, Fadiman, C. (ed) (New York: Simon & Schuster, New York, 1958), story originally published in 1940.
Kasner,
Edward and James Newman, Mathematics and the Imagination (
Pickover, Clifford, Surfing through Hyperspace (New York: Oxford University, Press, 1999).
Rucker, Rudy, The Fourth Dimension (Boston, Massachusetts: Houghton-Mifflin, 1984).
Tangherlini, F., "Atoms in Higher Dimensions," Nuovo Cimento 27: 636-639 (1963).
Tegmark, Max, "On the Dimensionality of Spacetime," Classical and Quantum Gravity 14: L69-L75 (1997).
Velleman, Dan, "Rubik's Tesseract," Mathematics Magazine, February 65(1): 27-36 (1992).
Peano Axioms (1889)
Kennedy, Hubert C., "The Origins of Modern Axiomatics: Pasch to Peano," The American Mathematical Monthly, 79(2): 133-136 (February 1972).
Kennedy, Hubert C, Peano: Life and Works of Giuseppe Peano (New York: Springer, 1980).
"Peano Axioms," BookRags; see http://www.bookrags.com/research/peano-axioms-wom/.
Peano, Giuseppe, Arithmetices principia, nova methodo exposita (The Principles of Arithmetic, Presented by a New Method) (Turin: Bocca, 1889).
Peano Curve (1890)
Bartholdi, John J., III, Georgia Institute of Technology, "Some Combinatorial Applications of Space-filling Curves"; see http://www2.isye.gatech.edu/~jjb/.
Darling, David, The Universal Book of Mathematics (
Gardner, Martin, Penrose Tiles to Trapdoor Ciphers. (Washington DC: The Mathematical Association of America, revised edition, 1997).
Mandelbrot, Benoit, The Fractal Geometry of Nature (New York: W. H. Freeman, 1982).
Platzman, Loren K. and John J. Bartholdi, III, "Spacefilling Curves and the Planar Traveling Salesman Problem," Journal of the Association of Computing Machinery 36(4): 719-737 (1989).
Sagan, Hans, Space-Filling Curves (New York: Springer-Verlag 1994).
Vilenkin, Naum Yakovlevich, In Search of Infinity (New York: Springer 1995).
Wallpaper Groups (1891)
♪ Branko Grünbaum in "What Symmetry Groups are
Present in the
S. J. Abas notes that, "Although Escher was correct that the
Moorish artists restricted their tessellations to mosaics of non-figurative
shapes, there was not a total prohibition of life-like pictures. Indeed works
by Moorish artists that show scenes of battles, lion hunt, boar hunt, council
meeting and other events can be found in the very
Abas, S. Jan, "Islamic Patterns:
The Spark in Escher's Genius," in M.C. Escher's Legacy: A Centennial Celebration,
Michele Emmer and Doris Schattschneider, editors (
Barlow, W. "Über die geometrische Eigenschaften homogener starrer Strukturen," Z. Kryst. Min., 23: 1-63 (1894).
Conway, John H., "The Orbifold Notation for Surface Groups," in M. W. Liebeck and J. Saxl (editors), Groups, Combinatorics and Geometry, Proceedings of the L.M.S. Durham Symposium, July 5–15, Durham, UK, 1990; London Math. Soc. Lecture Notes Series 165 (Cambridge: Cambridge University Press, 1992), pp. 438-447.
Coxeter, H. S. M., Introduction to Geometry, Second Edition (Hackensack, New Jersey: John Wiley & Sons, 1969).
Darling, David, The Universal Book of Mathematics (
Fedorov, E. S. "The elements of the Study of Figures," [Russian] Zapiski Imperatorskogo S. Peterburgskogo Mineralogichesgo Obshchestva (Proc. S. Peterb. Mineral. Soc.), 21(2): 1-289 (1885).
Gardner, Martin, New Mathematical Diversions (Washington DC: The Mathematical Association of America, 1995), quotes H. S. M. Coxeter.
Grünbaum, Branko, "What Symmetry Groups are Present in the
Schoenflies, A. M., "Über Gruppen von Bewegungen," Mathematische Annalen, 28: 319-342 (1886), and 29: 50-80 (1887).
Sylvester's Line Problem (1893)
Erdos, Paul, "Problem 4065," American Mathematical Monthly 50: 65 (1943).
Malkevitch, Joseph, "A Discrete Mathematical Gem," American Mathematical Society; see http://e-math.ams.org/featurecolumn/archive/sylvester1.html.
Melchior, E., "Über Vielseite der projektiven Ebene," Deutsche Math. 5: 461–475 (1940). (In 1940, E. Melchior provided a proof of a statement equivalent to the Sylvester–Gallai theorem.)
Steinberg, R., Buck, R. C., Grünwald, T. (Tibor Gallai) and Steenrod, N. E. "Three Point Collinearity (solution to problem 4065)," American Mathematical Monthly 51: 169–171(1944). (Tibor Gallai's name was originally Tibor Grünwald.)
Sylvester, James J., "Mathematical Question 11851," Educational Times 59: 98 (1893).
Proof of the Prime Number Theorem (1896)
♪ Note that the symbol π is used here to represent a function and does not refer to the mathematical constant 3.1415….
Bays, Carter, and Hudson, Richard H., "A New Bound for the Smallest x with π(x)>li(x)," Mathematics of Computation, 69(231): 1285-1296 (2000).
Havil, Julian, Gamma: Exploring Euler's Constant (
Littlewood, John Edensor, "Sur la distribution des nombres premiers," Comptes Rendus 158: 1869-1872 (1914).
Skewes, Stanley, "On the Difference π(x) − li(x),"
Journal of the
Skewes, Stanley, "On the difference π(x) − li(x)
(II)," Proceedings of the London Mathematical Society,
Weisstein, Eric W., "Prime Counting Function," From MathWorld--A Wolfram Web Resource; see http://mathworld.wolfram.com/PrimeCountingFunction.html.
Zagier, Don, "The First 50 Million Prime Numbers," Mathematical Intelligencer, 0: 7-19 (1977). (The quote from German mathematician Don Zagier was first spoken at a 1975 lecture.)
Pick's Theorem (1899)
Darling, David, The Universal Book of Mathematics (
Funkenbusch, W. W., "From Euler's Formula to Pick's Formula using an Edge Theorem," The American Mathematical Monthly, 81(6): 647-648 (1974).
Grünbaum, Branko and G. C. Shephard, "Pick's Theorem," The American Mathematical Monthly, 100(2): 150-161 (1993).
Pick, Georg, "Geometrisches zur Zahlenlehre, " Sitzungber. Lotos, Naturwissen Zeitschrift Prague, 19: 311-319 (1899).
Varberg, Dale E., "Pick's Theorem Revisited," The American Mathematical Monthly, 92(8): 584-587 (1985).
Morley's Trisector Theorem (1899)
♪ Note that John Conway has also recently presented a simple proof of Morley's Theorem. Readers may wish to study a presentation of this proof in Appendix 5 of Siobhan Roberts' King of Infinite Space.
Connes, Alain, "A New Proof of Morley's Theorem," Publications Mathematiques de l'IHÉS, 88: 43-46 1998).
Connes, Alain,
"Symmetries,"
David, Wells, The Penguin Dictionary of Curious and Interesting Geometry (London: Penguin, 1991).
Francis, Richard L., "Modern Mathematical Milestones: Morley's Mystery," Missouri Journal of Mathematical Sciences, 14(1) (Winter, 2002); see http://www.math-cs.cmsu.edu/~mjms/2002.1/francis9.pdf.
Morley, Frank, "On Reflexive Geometry," Transactions of the American Mathematical Society, 8(1): 14-24 (1907).
Morley, Frank, My One Contribution to Chess (New York: B. W. Huebsch, 1945).
Peters, J. W., "The Theorem of Morley," National Mathematics Magazine, 16(3): 119-126 (December 1941).
Roberts, Siobhan, King of Infinite Space:
Donald Coxeter, the Man Who Saved Geometry (
Hilbert's 23 Problems (1900)
Hilbert, David, "Mathematical Problems," Bulletin of the American Mathematical Society, 8: 437-479 (1901-1902).
Yandell, Ben, Honors Class: Hilbert's
Problems and Their Solvers (
Chi-Square (1900)
Plackett, R. L., "Karl Pearson and the Chi-Squared Test," International Statistical Review / Revue Internationale de Statistique, 51(1): 59-72 (1983).
Schell, Michael J., Baseball's All-Time Best Hitters: How Statistics Can Level the Playing Field (Princeton, New Jersey: Princeton University Press, 1999).
Urdan, Timothy C., Statistics in Plain
English, Second Edition (
Boy's Surface (1901)
Boy, Werner, "Über die Curvatura integra und die Topologie geschlossener Flächen," Mathematische Annalen, 57: 151-184 (1903).
Jackson, Allyn, "Communications -- The World of Blind Mathematicians," Notices of the American Mathematical Society, 49(10): 1246-1251 (2002).
Barber Paradox (1901)
Joyce, Helen, "Mathematical Mysteries: The Barber's Paradox," Plus magazine; see http://plus.maths.org/issue20/xfile/index.html.
Russell, Bertrand, "Mathematics and the Metaphysicians" (1901), printed with the title "Recent Work in the Philosophy of Mathematics" in The International Monthly, reprinted in Mysticism and Logic and Other Essays (London: G. Allen & Unwin, 1917).
Sainsbury, R. M., Paradoxes, Second Edition (Cambridge: Cambridge University Press, 1995).
Jung's Theorem (1901)
Dekster, B. V., "The Jung Theorem for the Spherical and Hyperbolic Spaces," Acta Mathematica Hungarica, 67(4): 315–331 (1995).
Dekster, B. V., "The Jung Theorem in Metric Spaces of Curvature Bounded Above," Proceedings of the American Mathematical Society 125(8): 2425–2433 (1997).
Jung, Heinrich W. E. "Über die kleinste Kugel, die eine räumliche Figur einschliesst, " Journal für die Reine und Angewandte Mathematik (Journal for Pure and Applied Mathematics), 123: 241-257 (1901).
O'Connor, John J., and Robertson, Edmund F., "Heinrich Wilhelm Ewald Jung,"
at "The MacTutor History of Mathematics Archive"; see http://www-history.mcs.st-andrews.ac.uk/Biographies/Jung.html.
Smarandache, Florentin, "A
Generalization in Space of Jung's Theorem," Gazeta Matematica (
Wells, David, The Penguin Dictionary of Curious and Interesting Geometry, (New York: Penguin, 1992).
Poincare Conjecture (1904)
Mackenzie, Dana, "Breakthrough of the
Year: the Poincare Conjecture—Proved," Science,
314(5807): 1848-1849,
Nasar, Sylvia and David Gruber, "Manifold
Destiny: A Legendary Problem and the
O'Shea, Donal, The Poincare Conjecture:
In Search of the Shape of the Universe (
"Poincare Conjecture," Clay Mathematics Institute; see http://www.claymath.org/millennium/Poincare_Conjecture/.
Koch Snowflake (1904)
Koch, Helge von, "Sur une courbe continue sans tangente, obtenue par une construction geometrique elementaire" ("On a Continuous Curve Without Tangents Constructible from Elementary Geometry"), Arkiv for Matematik, Astronomi och Fysik, 1: 681-702, (1904).
Koch, Helge von, "Une methode geometrique elementaire pour l'etude de certaines questions de la theorie des courbes planes," Acta Mathematica, 30: 145-174 (1906).
Mandelbrot, Benoit, The Fractal Geometry of Nature (New York: W. H. Freeman, 1982).
Zermelo's Axiom of Choice (1904)
Darling, David, The Universal Book of Mathematics (
Howe, Denis, "Axiom of Choice"; see http://foldoc.org/index.cgi?query=axiom+of+choice.
Schechter, Eric, Mathematics Department,
Zermelo, Ernst, "Beweis, dass jede Menge wohlgeordnet werden kann," Mathematische Annalen 59: 514-516 (1904).
Jordan Curve Theorem (1905)
Hales, Thomas C., "Jordan's Proof of the Jordan Curve Theorem," a chapter in the book From Insight to Proof: Festschrift in Honour of Andrzej Trybulec, Studies In Logic, Grammar and Rhetoric, edited by Roman Matuszewski, Anna Zalewska, University of Bialystok, Bialystok, Poland, 10(23): 151-165 (2007).
Jordan, Camille, Cours d'Analyse de l'École Polytechnique, Deuxième eidition, entièrement refondue, Vol. I. (Paris : Gauthier-Villars, 1893).
Veblen, Oswald, "Theory on Plane Curves in Non-Metrical Analysis Situs," Transactions of the American Mathematical Society 6: 83–98 (1905).
Thue-Morse Sequence (1906)
Griswold, Ralph, "The Morse-Thue Sequence," The University of Arizona, 2001; see http://www.cs.arizona.edu/patterns/weaving/webdocs/gre_mt.pdf.
Moretti, Luigi and Vito Mocella, "Two-Dimensional Photonic Aperiodic
Morse, Marston, "Recurrent Geodesics on a Surface of Negative Curvature," Trans. Amer. Math. Soc. 22: 84-100 (1921).
Pickover, Clifford, "The Drums of Ulupu," in Mazes for the Mind (New York: St. Martin's Press, 1992).
Thue, Axel, "Über unendliche Zeichenreihen," Norske vid. Selsk. Skr. Mat. Nat. Kl. 7, 1-22 (1906). Reprinted in Selected Mathematical Papers of Axel Thue (edited by T. Nagell) (Oslo: Universitetsforlaget, 1977), pp. 139-158.
Brouwer Fixed-Point Theorem (1909)
Beran, Max,
Brouwer, Luitzen E. J., " Über eineindeutige, stetige Transformationen von Flächen in sich," Mathematische Annalen, 69: 176–180 (1910).
Darling, David, The Universal Book of
Mathematics (
Gale, David, "The Game of Hex and Brouwer Fixed-Point Theorem," The American Mathematical Monthly 86: 818-827 (1979).
Normal Number (1909)
Borel, Émile, "Les probabilites denombrables et leurs applications arithmetiques," Rendiconti Del Circolo Matematico Di Palermo, 27: 247-271 (1909).
Champernowne,
David G., "The Construction of Decimals
Darling,
David, The Universal Book of Mathematics (
Sierpinski, Wacław, "Demonstration elementaire du theorème de M. Borel sur les nombres absolument normaux et determination effective d'une tel nombre," Bulletin de la Societe Mathematique de France 45: 125-132 (1917).
Boole's Philosophy and Fun of Algebra (1909)
Boole, George, An Investigation of the Laws of Thought, on Which are Founded the Mathematical Theories of Logic and Probabilities. (London: Walton and Maberley, 1854).
Boole, Mary E., Philosophy and Fun of Algebra (London: C.W. Daniel, 1909).
Michalowicz, K. D. A., "Mary Everest Boole (1832-1916): An Erstwhile Pedagogist for Contemporary Times," in Vita Mathematica: Historical Research and Integration with Teaching, Ronald Calinger, editor (Washington, D.C.: Mathematical Association of America, 1996).
Peterson, Ivars, "Algebra, Philosophy, and
Fun," The Mathematical Association of
Principia Mathematica (1910-1913)
"The Modern Library's Top 100 Nonfiction
Books of the Century," The
Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 volumes, (Cambridge: Cambridge University Press, 1910, 1912, and 1913), second edition, 1925 (Volume 1), 1927 (Volumes 2 and 3). Abridged as Principia Mathematica to *56, (Cmabridge: Cambridge University Press, 1962).
Hairy Ball Theorem (1912)
Brouwer, Luitzen E. J., "Über Abbildung von Mannigfaltigkeiten," Mathematische Annalen, 71(4): 598 (1912).
Choi, Charles Q., "Structured Settings: Novel Techniques Expand the Nanotech Tool Kit," Scientific American, May 2007; see http://www.sciam.com/article.cfm?&articleID=E73CE5A8-E7F2-99DF-3872BE4E8D000E8F.
DeVries, Gretchen A., Markus Brunnbauer, Ying Hu, Alicia M. Jackson, Brenda Long, Brian T. Neltner, Oktay Uzun, Benjamin H. Wunsch and Francesco Stellacci, "Divalent Metal Nanoparticles," Science, 315(5810): 358 – 361 (January 19, 2007).
Eisenberg,
Infinite Monkey Theorem (1913)
♪
In 2003, researchers at the
Note that the use of the term "almost surely" in the first sentence of this entry is a mathematical way of saying that the monkey will type a finite text with probability one, assuming we allow an infinite number of trials.
Borel, Émile, "Mecanique Statistique et Irreversibilite," J. Phys., 5e serie, 3: 189–196 (1913).
Eddington, Arthur, The Nature of the Physical World: The Gifford Lectures (New York: Macmillan, 1928).
Pickover, Clifford, A Beginner's Guide
to Immortality (
Bieberbach Conjecture (1916)
Darling, David, The Universal Book of Mathematics (
de Branges, Louis, "A Proof of the Bieberbach Conjecture," Acta Matematica, 154(1-2): 137-152 (1985).
Mehrtens, Herbert, "Ludwig Bieberbach and Deutsche Mathematik," in Esther R. Phillips, editor, Studies in the History of Mathematics (Washington DC: The Mathematical Association of America, 1987), 195-241. (This is the source for the Bierberbach quote on the Jews.)
Sabbagh, Karl, "The Strange Case of Louis
de Branges," London Review of Books, 26(14),
Johnson's Theorem (1916)
Johnson, Roger, Johnson's Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle (Boston: Houghton Mifflin, 1929).
Johnson, Roger, "A Circle Theorem," The American Mathematical Monthly, 23(5): 161-162 (1916).
Kimberling, Clark, "Roger Arthur
Johnson (1890-1954)"; see
http://faculty.evansville.edu/ck6/bstud/johnson.html.
Wells, David, The Penguin Dictionary of Curious and Interesting Geometry, (New York: Penguin, 1992).
Hausdorff Dimension (1918)
Besicovitch, Abram S., "On Linear Sets of Points of Fractional Dimensions," Mathematische Annalen, 101: 161-193 (1929).
Darling, David, The Universal Book of Mathematics (
Hausdorff, Felix, "Dimension und äußeres Maß," Mathematische Annalen 79(1-2): 157-179 (March, 1919).
Mandelbrot, Benoit, The Fractal Geometry of Nature (New York: W. H. Freeman, 1982).
Brun's Constant (1919)
Brun, Viggo, "La serie 1/5 +1/7 + 1/11 +1/13 + …, es denominateurs sont nombres premiers jumeaux est convergente où finie," Bulletin des Sciences Mathematiques. 43: 124-128 (1919).
Nicely, Thomas, "Enumeration to 1014 of the Twin Primes and Brun's Constant," Virginia Journal of Science, 46(3): 195-204 (1995).
Peterson, Ivars, "Prime Twins," The Mathematical Association
of America,
Granville, Andrew, "International Team Shows that Primes Can Be Found in Surprising Places" (AMS news release of December 5, 1997), reprinted in the March 1998, Resonance (a journal of science education), 3(3):71-72 (March, 1998).
Googol (c. 1920)
♪ Interestingly, scholarly sources are sometimes divided as to the birthday of Sirotta (e.g. 1911 or 1929) and the date that googol was first coined (1920 or 1938.)
Kasner, Edward and Newman, James R., Mathematics
and the Imagination (London: Penguin, 1940; New York: Simon and Schuster,
1967), reprinted by
Pickover, Clifford, Keys to Infinity (Hoboken, New Jersey: John Wiley & Sons, 1995)
Antoine's Necklace (1920)
Alexander, James W., "An Example of a Simply Connected Surface Bounding a Region Which Is Not Simply Connected," Proceedings of the National Academy of Sciences, 10: 8-10 (1924). (Discusses Alexander's Horned Sphere.)
Antoine, Louis, "Sur la possibilite d'etendre Vhomeomorphie de deux figures à leurs voisinages," C. R. Acad. Sci. Paris, 171: 661-663 (1920).
Antoine, Louis, "Sur L'homeomorphisme de Deux Figures et de leurs Voisinages," J. Math. Pures et Appl., 4: 221-325 (1921).
Brechner, Beverly L. and Mayer, John C., "Antoine's Necklace or How to Keep a Necklace from Falling Apart," College Mathematics Journal, 19(4): 306-320 (1988).
Jackson, Allyn, "Communications -- The World of Blind Mathematicians," Notices of the American Mathematical Society, 49(10): 1246-1251 (2002).
Weisstein, Eric W., "Antoine's Necklace," from MathWorld--A Wolfram Web Resource; see http://mathworld.wolfram.com/AntoinesNecklace.html.
Noether's Idealtheorie (1921)
Case,
Bettye Anne and Anne M. Leggett, Complexities: Women in Mathematics (
Noether, Emmy, "Idealtheorie in Ringbereichen," Mathematische Annalen, 83: 24–66 (1921).
Noether, Emmy, "Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkopern," Mathematische Annalen, 96: 26–61 (1926).
Roberts, Siobhan, King of Infinite
Space: Donald Coxeter, the Man Who Saved Geometry (
Lost in Hyperspace (1921)
Alexanderson, Gerald L., The Random Walks of George Pólya
(
Asimov, Daniel, "There's No Space Like Home," The Sciences, 35(5): 20-25 (Sept./Oct. 1995).
McCrea, W. H.
and Whipple, F. J. W., "Random Paths in Two and Three Dimensions," Proceedings
of the Royal Society of
Geodesic Dome (1922)
Baldwin, James T., Buckyworks: Buckminster Fuller's Ideas for Today (Hackensack, New Jersey: John Wiley& Sons, 1996).
Zung, Thomas T. K., Buckminster Fuller:
Anthology for a New Millennium (
Alexander's Horned Sphere (1924)
Alexander, James W., "An Example of a Simply Connected Surface Bounding a Region Which Is Not Simply Connected," Proceedings of the National Academy of Sciences, 10: 8-10 (1924). (Discusses Alexander's Horned Sphere.)
Browne, Cameron, "Cameron's Art Page"; see http://members.optusnet.com.au/cameronb/art/art-1.htm.
Gardner, Martin, Penrose Tiles to Trapdoor Ciphers (Washington DC: The Mathematical Association of America, revised edition, 1997).
Pickover, Clifford, The Mobius Strip
(
Banach-Tarski Paradox (1924)
Banach, Stefan and Tarski, Alfred, "Sur la decomposition des ensembles de points en parties respectivement congruentes," Fundamenta Mathematicae, 6: 244-277 (1924).
Darling, David, The Universal Book of Mathematics (
Robinson, Raphael M. "On the Decomposition of Spheres," Fund. Math. 34: 246-260 (1947).
Stromberg, Karl, "The Banach-Tarski Paradox," The American Mathematical Monthly, 86(3): 151-161 (March 1979).
Wagon, Stan, The Banach-Tarski Paradox (New York: Cambridge University Press, 1993).
Squaring a Rectangle (1925)
Brooks, R .L., C. A. B. Smith, A. H. Stone, and W. T. Tutte, "The Dissection of Rectangles into Squares," Duke Mathematical Journal, 7: 312-40 (1940).
Duijvestijn,
A. J. W., "
Moroń, Zbigniew, "O rozkladach prostokatów na kwadraty" ("On the Dissection of a Rectangle into Squares"), Przeglad matematyczno-fizyczny, 3: 152-153 (1925).
Gardner, Martin, "Squaring the Square," in The Second Scientific American Book of Mathematical Puzzles & Diversions: A New Selection. (New York: Simon and Schuster, 1961).
Stewart, Ian, Math Hysteria (
"Zbigniew Moroń (1904-1971),
Hilbert's Grand Hotel (1925)
♪ Note that there are certain levels or classes of infinity that the Hilbert's Grand Hotel may not be able to accommodate. Georg Cantor showed that there are infinities too big to be counted, which is essentially what happens when we associate each guest with a room number.
The precise date and origin of Hilbert's Hotel is difficult to determine. Hilbert spoke of this hotel during his lectures in the 1920s, but he did not appear to write about it. His paper "On the Infinite" was delivered in 1925. Hilbert's Hotel came to wider public attention in George Gamow's entertaining book One, Two, Three... Infinity, originally published in 1947 and revised in 1961. Gamow writes that the Hilbert's Hotel appeared in Richard Courant's unpublished The Complete Collection of Hilbert Stories. Richard Courant (1888–1972) was a German American mathematician and assistant to Hilbert in Gottingen.
Erickson, Glenn W. and Fossa, John. A., Dictionary of Paradox. (Lanham, Maryland: University Press of America, 1998).
Falletta, Nicholas, The Paridoxicon (Hackensack, New Jersey: John Wiley& Sons, 1990).
Gamow, George, One, Two, Three...Infinity (New York: Viking Press, 1947).
Hilbert, David, "Über das Unendliche" (On the Infinite), Mathematische Annalen 95: 161-190 (1926), from a lecture given in Münster, June 1925. Reprinted in Paul Benacerraf and Hilary Putnam (editors), Philosophy of Mathematics: Selected Readings, Second Edition (Cambridge: Cambridge University Press 1983).
Menger Sponge (1926)
♪ To better visualize how we obtain the 400 cubes in the second-generation sponge, consider the six small cubes. From each of the six small cubes, we repeat the process, dividing each into 27 smaller cubes and removing the seven central cubes from each of them. This leaves 400 smaller cubes.
"Fractal Fragments," The Institute for Figuring; see http://www.theiff.org/oexhibits/menger01.html.
Mandelbrot, Benoit, The Fractal Geometry of Nature (New York: W. H. Freeman, 1982).
Menger, Karl, "Allgemeine Räume und Cartesische Räume" ("General Spaces and Cartesian Spaces"), Communications to the Amsterdam Academy of Sciences, 29: 476-482 and 1125-1128 (1926). English translation reprinted in Classics on Fractals, Gerald A. Edgar, editor, (Boston: Addison-Wesley Publishing Company, 1993).
"The Menger Sponge," The Institute for Figuring; see http://www.theiff.org/oexhibits/menger02.html.
Differential Analyzer (1927)
Bush, Vannevar, F. D. Gage, and H. R. Stewart, "A Continuous Integraph," Journal of the Franklin Institute, 203(1):63-84 (1927).
Bush, Vannevar and Harold Hazen, "Integraph Solutions of Differential Equations," Journal of the Franklin Institute, 204(5): 575-615 (1927).
Bush, Vannevar and Stewart H. Caldwell, "A New Type of Differential Analyzer," Journal of the Franklin Institute, 240(4): 255-326 (1945).
Bush, Vannevar, "As We May Think," July 1945 Atlantic Monthly; see http://www.theatlantic.com/doc/194507/bush.
Ramsey Theory (1928)
♪ Ramsey, a militant atheist, died at the age of 26 after an abdominal operation.
The mathematician Paul Erdos once commented on the difficulty of solving Ramsey problems with higher numbers: "Aliens invade the earth and threaten to obliterate it in a year's time unless human beings can find the Ramsey number for red five and blue five. We could marshal the world's best minds and fastest computers, and within a year we could probably calculate the value. If the aliens demanded the Ramsey number for red six and blue six, however, we would have no choice but to launch a preemptive attack."
Erdos, Paul and Szekeres, George, "On Some Extremum Problems in Elementary Geometry," Ann. Univ. Sci. Budapest Eotvos Sect. Math, 3-4: 53-62 (1961).
Graham, Ronald, Bruce Rothschild, and Joel Spencer, Ramsey Theory (Hackensack, New Jersey: John Wiley & Sons, NY, 1990).
Graham, Ronald and Joel Spencer, "Ramsey Theory." Scientific American, 263(1): 112-117 (July 1990).
Hoffman, Paul, The Man Who Loved Only Numbers (New York: Hyperion, 1999).
Ramsey, Frank P., "On A Problem of Formal Logic," Proc. London Math. Soc. Series 2, 30: 264-286 (1930), read to the society in 1928.
Godel's Theorem (1931)
♪ Godel demonstrated the incompleteness of the theory of Principia Mathematica, discussed in the entry Principia Mathematica (1910–1913).
Godel, Kurt, "Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I." ("On Formally Undecidable Propositions in Principia Mathematica and Related Systems I"), Monatshefte für Mathematik und Physik, 38: 173-98 (1931).
Hofstadter,
Pickover, Clifford, A Passion
for Mathematics (
Wang, Hao, Reflections on Kurt Godel (Cambridge, Massachusetts: MIT Press, 1990).
Champernowne's Number (1933)
Bailey, David H. and Richard E. Crandall, "On the Random Character of Fundamental Constant Expansions," Experimental Mathematics 10(2): 175-190 (2001).
Belshaw, Adrian and Peter Borwein, "Strong Normality of Numbers"; see http://www.cecm.sfu.ca/personal/pborwein/PAPERS/P211.pdf.
Champernowne, David G., "The Construction
of Decimals
Mahler, Kurt, "Arithmetische Eigenschaften einer Klasse von Dezimalbrüchen," Proc. Konin. Neder. Akad. Wet. Ser. A., 40: 421-428 (1937).
Von Baeyer, Hans Christian, Information
(
Bourbaki: Secret Society (1935)
Mashaal, Maurice, Bourbaki (
Aczel, Amir, The Artist and the
Mathematician: The Story of Nicolas Bourbaki, the Genius Mathematician Who
Never Existed (
Fields Medal (1936)
Monastyrsky,
Mikhail, Modern Mathematics in the Light of the
Fields Medals. (
Riehm, Carl, "The Early History of the Fields Medal," Notices of the American Mathematical Society, 49(7): 778-782 (2002).
Turing Machines (1936)
Copeland, B.
Jack (editor) The Essential Turing: Seminal Writings in Computing, Logic,
Philosophy, Artificial Intelligence, and Artificial Life plus The Secrets of
Enigma (
Leavitt, David, The
Man Who Knew Too Much: Alan Turing and the Invention of the Computer (
Turing, Alan, "On Computable Numbers with
an Application to the Entscheidungs Problem," Proceedings of the
Voderberg Tilings (1936)
Grünbaum, Branko and Shephard G. C., "Spiral Tilings and Versatiles," Mathematics Teaching, 88: 50-51 (September, 1979).
Grünbaum, Branko and G. C.
Shephard, Tilings and Patterns (
Rice, Marjorie and Schattschneider Doris, "The Incredible Pentagonal Versatile," Mathematics Teaching, 93: 52-53 (December, 1980).
Voderberg, Heinz, "Zur Zerlegung der Umgebung eines ebenen Bereiches in kongruente," Jahresbericht der Deutschen Mathematiker-Vereinigung, 46: 229-233 (1936).
Collatz Conjecture (1937)
Hayes, Brian, "Computer Recreations: On the Ups and Downs of Hailstone Numbers," Scientific American, 250(1): 10-16 (1984).
Lagarias, Jeffrey. C., "The 3x+1 Problem and Its Generalizations," American Mathematical Monthly, 92: 3-23 (1985).
Oliveira e Silva, Tomás, "Maximum Excursion and Stopping Time Record-Holders for the 3x+1 Problem: Computational Results," Mathematics of Computation, 68: 371-384 (1999).
Pickover, Clifford, Computers, Pattern, Chaos, and Beauty
(
Ford Circles (1938)
Ford, Lester, R., "Fractions," The American Mathematical Monthly, 45(9): 586-601 (1938).
Pickover, Clifford, Keys to Infinity (Hoboken, New Jersey: John Wiley & Sons, 1995).
The Rise of Randomizing Machines (1938)
Fisher, Ronald A., and Frank Yates, Statistical Tables for Biological, Agricultural and Medical Research (London: Oliver & Boyd, 1938).
Ford, Joseph, "How Random is a Coin Toss? Physics Today, 36: 40-47 (April 1983).
Hayes, Brian, "Randomness as a Resource," 89(4): 300-304 (July-August, 2001).
Herzog, Thomas N. and Graham Lord, Applications of Monte
Carlo Methods to Finance and Insurance (
Kelvin, Baron William Thomson, "Nineteenth
Century Clouds Over the Dynamical Theory of Heat and Light," The
Kelvin, Baron William Thomson,
Kendall, Maurice G. and Bernard Babington-Smith, "Second Paper on Random Sampling Numbers," Supplement to the Journal of the Royal Statistical Society, 6(1): 51-61 (1939).
Kendall, Maurice G. and Bernard Babington-Smith, Tables of Random Sampling Numbers (Cambridge, England: Cambridge University Press, 1939).
The Rand Corporation, A
Million Random Digits with 100,000
Tippett, Leonard H. C., "Random Sampling Numbers," Tracts for Computers, Volume 15 (London: Cambridge University Press, 1927).
Yule, G. Udny, "A Test of Tippett's Random Sampling Numbers," Journal of the Royal Statistical Society, 101: 167-172 (1938).
Birthday Paradox (1939)
Nandor, Mark, "The Inclusion of Leap Year to the Canonical Birthday Problem," The Mathematics Teacher, 97: 87-89 (2004).
Peterson, Ivars, "MathTrek: Birthday Surprises," Sciences
News (online),
Von Mises, Richard, "Über Aufteilungs--und Besetzungs-Wahrscheinlichkeiten," Revue de la Faculte des Sciences de l'Universite d'Istanbul, 4: 145-163 (1939), reprinted in Selected Papers of Richard von Mises, Volume 2, edited by P. Frank, S. Goldstein, M. Kac, W. Prager, G. Szego, and G. Birkhoff (Providence, Rhode Island: American Mathematical Society, 1964).
Polygon Circumscribing (c. 1940)
Bouwkamp, Christoffel, "An Infinite Product," Indagationes Mathematicae. 27(1): 40-46 (1965).
Haber, Heinz, "Das mathematische Kabinett," Bild der Wissenschaft, 2: 73 (April, 1964).
Kasner, Edward and James Newman, Mathematics and the
Imagination (
Pickover, Clifford, Keys to Infinity (Hoboken, New Jersey: John Wiley & Sons, 1995).
Hex (1942)
Gale, David, "The Game of Hex and Brouwer Fixed-Point Theorem," The American Mathematical Monthly 86: 818-827 (1979).
Nasar, Sylvia, A Beautiful Mind: The
Life of Mathematical Genius and Nobel Laureate John Nash (
Pig Game Strategy (1945)
Neller, Todd W. and
Neller, Todd W. and
Neller, Todd and
Neller, Todd W.,
Peterson, Ivars, "Playing Pig, Optimally," The Mathematical Association of America, May, 2004; see http://www.maa.org/mathland/mathtrek_05_31_04.html.
Scarne, John, Scarne on Dice (Harrisburg, Pennyslvania: Military Service Publishing Co., 1945). (Second edition published by New York: Crown Publishers, Inc., 1980).
Shi, Yixun, "The Game PIG: Making Decisions Based on Mathematical
Thinking," Teaching Mathematics and Its Applications 19(1): 30–34 (2000).
ENIAC (1946)
♪ Professor Jan Van der Spiegel's goal was to recreate the original ENIAC, following its architecture and basic circuit building blocks as much as possible. His team modeled vacuum tube circuits with transistors.
Hally, Mike, Electronic Brains: Stories from the Dawn of the
Computer Age (
Eckert, J. Presper and Mauchly, John, "Electronic Numerical Integrator and Computer," U.S Patent 3,120,606, filed in 1947, issued in 1964.
McCartney, Scott, ENIAC: The Triumphs and Tragedies of the World's First Computer (New York: Walker & Company, 1999).
Van der Spiegel, Jan, James F. Tau, Titiimaea F. Ala'ilima, and Lin Ping Ang, "The ENIAC -- History, Operation and Reconstruction in VLSI," in The First Computers: History and Architectures, edited by R. Rojas and U. Hashagen (Cambridge, Massachusetts: MIT Press, 2000).
Von Neumann's Middle-Square Randomizer (1946)
Hayes, Brian, "Randomness as a Resource," American Scientist, 89(4): 300-304 (July-August 2001); see http://www.americanscientist.org/template/AssetDetail/assetid/20829/.
Herzog, Thomas N. and Graham Lord, Applications of Monte
Carlo Methods to Finance and Insurance (
Kendall, Maurice G. and Bernard Babington-Smith, "Second Paper on Random Sampling Numbers," Supplement to the Journal of the Royal Statistical Society, 6(1): 51-61 (1939).
Matsumoto, Makoto and Takuji Nishimura, "Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudorandom Number Generator,"ACM Transactions on Modeling and Computer Simulation, 8(1): 3-30 (1998).
Matsumoto, Makoto and Yoshiharu Kurita, "Twisted GFSR Generators," ACM Transactions on Modeling and Computer Simulation, 2(3): 179-194 (1992).
von Neumann, John, "Principles of Large-Scale
Computing Machines," paper delivered by von Neumann on
von Neumann, John, "Various Techniques Used In Connection with Random Digits," In Collected Works, Vol. 5 (New York: Pergamon Press, 1951), pp. 768-770.
von Neumann, John, "Various Techniques
Used in Connection with Random Digits," Applied Mathematics Series,
Gray Code (1947)
Gray, Frank, "Pulse Code Communication,"
"What are Gray Codes, and Why Are They Used?"; see http://www.faqs.org/faqs/ai-faq/genetic/part6/section-1.html.
Information Theory (1948)
Shannon, Claude, "A Mathematical Theory of Communication," Bell System Technical Journal, 27: 379–423, 623–656 (July and October, 1948).
Tallack, Peter, The Science Book (
Curta Calculator (1948)
♪ More accurately, Herzstark was a "half-Jew," as one Nazi referred to him when Herzstark tried to protect his friends from the Gestapo. His father was Jewish and his mother Catholic. Because of the family business, he was familiar with calculators since childhood.
Herzstark worked on the Curta design while
a prisoner, and the Americans liberated the
Furr, Rick, "The Curta Calculator Page"; see http://www.vcalc.net/cu.htm.
Ifrah, Georges, The Universal
History of Computing: From the Abacus to the Quantum Computer (
Saville, Greg, "Curta Calculators"; see http://home.teleport.com/~gregsa/curta/.
Stoll, Cliff, "The Curious History of the First Pocket Calculator," Scientific American, 290(1): 92–99 (January, 2004).
Császár Polyhedron (1949)
Császár, Ákos, "A Polyhedron without Diagonals," Acta Univ Szegendiensis, Acta Scient. Math, 13: 140-142 (1949). (Interestingly, this paper has no figures, which may explain why this did not stimulate further work until the 1970s.)
Darling, David, The Universal Book of Mathematics (
Gardner, Martin, Time Travel and other Mathematical Bewilderments (New York: Freeman: 1987).
Reinhardt, Curt, "Zu Mobius Polyedertheorie, " Berichte der K. Sachs. Gesellschaft der Wissenschaften, Math. Phys. Klasse 37: 106-125 (March 1885).
Nash Equilibrium (1950)
Morgenstern, Oskar and John von Neumann, Theory of Games and Economic Behavior (Princeton, New Jersey: Princeton University Press, 1944).
Nasar, Sylvia, A Beautiful Mind (New York, Simon & Schuster, 1998).
Nash, John, "Equilibrium Points in n-person Games," Proceedings of the National Academy of Sciences 36(1): 48-49 (1950).
Nash, John, "Non-Cooperative Games," The Annals of Mathematics, 54(2): 286-295 (1951).
Tallack, Peter, The Science
Book (
Coastline Paradox (c. 1950)
Mandelbrot, Benoît, "How Long Is the Coast of
Pickover, Clifford, Computers, Pattern, Chaos, and Beauty
(
Richardson, Lewis F., Statistics of Deadly Quarrels (Pacific
Grove, California: Boxwood Press, 1960). A first version was published in 1950
and another in 1953. Earlier works of
Prisoner's Dilemma (1950)
Dresher, Melvin, The Mathematics of Games of Strategy: Theory and Applications (Englewood Cliffs, New Jersey: Prentice-Hall, 1961).
Flood, Merrill M., "Some Experimental Games," Research Memorandum
RM-789. RAND Corporation,
Flood, Merrill M., "Some Experimental Games," Management Science, 5(1): 5-26 (Oct., 1958).
Pickover, Clifford, The Paradox of God and the Science of
Omniscience (
Poundstone, William, Prisoner's Dilemma (New York: Doubleday, 1992).
Cellular Automata (1952)
Schiff, Joel, Cellular Automata (
Toffoli, Tommaso and Norman Margolus, Cellular Automata Machines (Cambridge, Massachusetts: MIT Press, 1987).
von Neumann, John, Theory of Self-Reproducing Automata, edited and completed by Arthur W. Burks (Urbana: University of Illinois Press, 1966).
Wolfram, Stephen,
A New Kind of Science (
Martin Gardner's Mathematical Recreations (1957)
Berlekamp, Elwyn R., John H. Conway, and Richard K. Guy, Winning Ways for Your Mathematical Plays (Burlington, Massachusetts: Elsevier, 1982). Originally published by Academic Press, which is now part of Elsevier.
Frazier, Kendrick, "A Mind at Play: An Interview with Martin Gardner," Skeptical Inquirer, 22(2): 34-39 (March/April 1998).
Gardner, Martin, Mathematical Carnival (New York: Vintage, 1977).
Gardner, Martin, The Sixth Book of Mathematical Games from Scientific American (Chicago: University of Chicago Press, 1984).
Gardner, Martin, Time Travel and other Mathematical Bewilderments (New York: Freeman, 1987).
Gardner, Martin, Mathematical Magic Show (Washington, DC: Mathematical Association of America, 1989).
Gardner, Martin, New Mathematical Diversions (Washington DC: The Mathematical Association of America, 1995).
Gardner, Martin, Penrose Tiles to Trapdoor Ciphers. (Washington DC: The Mathematical Association of America, revised edition, 1997).
Gardner, Martin, Martin Gardner's
Mathematical Games (CD-ROM) (
Jackson, Allyn, "Interview with Martin Gardner," Notices of the American Mathematical Society, 52(6): 602-611 (June/July 2005).
Gilbreath's Conjecture (1958)
♪ Norman Gilbreath told me in a personal communication that "Erdos believed my conjecture is probably true and it will be 200 years before it is proved."
Guy, Richard, "The Strong Law of Small Numbers," American Mathematical Monthly, 95(8): 697-712 (October, 1988).
Guy, Richard, "The Second Strong Law of Small Numbers," Mathematics Magazine, 63(1): 3-20 (February, 1990).
Guy, Richard, "Gilbreath's Conjecture," in Unsolved Problems in Number Theory, Second Edition (New York: Springer-Verlag, 1994).
Odlyzko, Andrew, "Iterated Absolute Values of Differences of Consecutive Primes," Mathematics of Computation, 61(203): 373-380 (1993).
Turning a Sphere Inside Out (1958)
♪ Note that although sphere eversion is theoretically possible, a circle cannot be turned inside out.
Francis, George K. and Morin, Bernard, "Arnold Shapiro's Eversion of the Sphere," Mathematical Intelligencer 2: 200-203 (1979).
Levy, Silvio,
Delle Maxwell, and Tamara Munzner, "Outside In," (Wellesley, MA: AK Peters,
1994), a very educational narrated video (21 minutes) from the
Max, Nelson, "Turning a Sphere Inside Out" (videotape), (Chicago: International Film Bureau, 1977).
Phillips, Anthony, "Turning a Surface Inside Out," Scientific American, 214: 112-120. (May, 1966), 112-120.
Stephen, Smale, "A Classification of Immersions of the Two-Sphere," Transactions of the American Mathematical Society 90(2): 281-290 (1958).
Sullivan, John M., George Francis, and Stuart Levy, "The Optiverse: A Video"; see http://new.math.uiuc.edu/optiverse/.
Platonic Billiards (1958)
Cipra, Barry, "Mathematics: How to Play Platonic Billiards," Science, 275(5303): 1070 (February 1997).
Gardner, Martin, Sixth Book of Mathematical Games from Scientific American, (New York: W. H. Freeman, 1971).
Steinhaus, Hugo, One Hundred Problems in Elementary Mathematics (New York: Basic Books, 1964), problem 33. (The book is a translation of the 1958 Polish edition.)
Outer Billiards (1959)
Cipra,
Barry, "Bizarre Pool Shots Spiral to Infinity," Science, 317(5834): 39 (
Gutkin, Eugene and N. Simanyi, "Dual Polygonal Billiard and Necklace Dynamics," Comm. Math. Phys. 143: 431–450 (1991).
Moser, Jürgen, "Stable and Random Motions in Dynamical Systems, with Special Emphasis on Celestial Mechanics," Annals of Math Studies, No. 77, (Princeton New Jersey: Princeton University Press, 1973).
Moser, Jürgen, "Is the Solar System Stable?" Mathematical Intelligencer 1: 65-71 (1978).
Neumann, B. H., "Sharing Ham and Eggs" (summary
of a Manchester Mathematics Colloquium,
Schwartz, Richard Evan, "Outer Billiards on Kites"; see http://www.math.brown.edu/~res/Papers/kite2.pdf.
Newcomb's Paradox (1960)
♪ In 1969, Robert Nozick said about Newcomb's Paradox, "To almost everyone, it is perfectly clear and obvious what should be done. The difficulty is that these people seem to divide almost evenly on the problem, with large numbers thinking that the opposing half is just being silly."
Nozick, Robert, "Newcomb's Problem and Two principles of Choice," in Essays in Honor of Carl G. Hempel, edited by Nicholas Rescher (Dordrecht: D. Reidel, 1969).
Gardner, Martin (1974), "Newcomb's Paradox," in The
Colossal Book of Mathematics (
Pickover, Clifford, The Paradox of God and the Science of
Omniscience (
Sierpiński Numbers (1960)
Jaeschke, G., "On the Smallest k such that k · 2n +1 are Composite," Math. Comp., 40(181): 381-384 (1983).
Peterson,
Ivars, "A Remarkable Dearth of Primes," The Mathematical Association
of America,
"Seventeen or Bust: A Distributed Attack on the Sierpinski Problem"; see http://www.seventeenorbust.com/.
Sierpiński, Wacław, "Sur un problème concernant les nombres k.2n + 1," Elem. Math. 15: 73-74 (1960).
Zagier, Don, "The First 50 Million Prime Numbers," Mathematical Intelligencer, 0: 7-19 (1977).
Chaos and the Butterfly Effect (1963)
Gleick, James, Chaos: Making a New Science (New York: Penguin, 1988).
Lorenz, Edward N., "Deterministic Nonperiodic Flow," Journal of Atmospheric Sciences, 20: 130-141 (1963).
Lorenz, Edward N., The Essence of Chaos (Seattle: University of Washington Press, 1996).
Pickover, Clifford, Computers,
Pattern, Chaos, and Beauty (
Ulam Spiral (1963)
Gardner, Martin, The Sixth Book of Mathematical Games from Scientific American (Chicago: University of Chicago Press, 1984).
Stein, M. and Ulam, Stanisław, M., "An Observation on the Distribution of Primes," The American Mathematical Monthly, 74(1): 43-44 (1967).
Stein, M. L., Ulam, Stanisław, M., and Wells, M. B., "A Visual Display of Some Properties of the Distribution of Primes," The American Mathematical Monthly, 71(5): 516-520 (1964).
Continuum Hypothesis Undecidability (1963)
♪ Recent work by mathematician W. Hugh Wooden may suggest the possibility that the continuum hypothesis is false, and, indeed, the hypothesis continues to remain a hot topic of contemporary research.
Cohen, Paul J., Set Theory and the Continuum Hypothesis (New York: W. A. Benjamin, 1966).
Cohen, Paul J., "The
Cohen, Paul J., "The
Godel, Kurt, The Consistency of the Continuum-Hypothesis (Princeton, New Jersey: Princeton University Press, 1940).
Godel, Kurt, "What is Cantor's Continuum Problem?", American Mathematical Monthly 54: 515–525 (1947). Reprinted in Paul Benacerraf and Hilary Putnam (editors), Philosophy of Mathematics: Selected Readings, Second Edition (Cambridge: Cambridge University Press 1983).
Pickover, Clifford, A Passion
for Mathematics (
Woodin, W. Hugh, "The Continuum Hypothesis, Part I," Notices of the American Mathematical Society 48(6): 567–576 (2001).
Woodin, W. Hugh, "The Continuum Hypothesis, Part II," Notices of the American Mathematical Society 48(7): 681–690 2001).
Superegg (c. 1965)
Gardner, Martin, "Piet Hein's Superellipse," Mathematical Carnival. A New Round-Up of Tantalizers and Puzzles from Scientific American (New York: Vintage Press, 1977).
Moscovich, Ivan, Leonardo's Mirror
& Other Puzzles (
Fuzzy Logic (1965)
Tanaka, Kazuo, An Introduction to Fuzzy Logic for Practical Applications (New York: Springer, 1996).
Zadeh, Lotfi, "Fuzzy Sets," Information and Control, 8: 338-353 (1965).
Zadeh, Lotfi, "Fuzzy Sets as a Basis for a Theory of Possibility," Fuzzy Sets and Systems 1: 3–28 (1978).
Instant Insanity (1966)
Armbruster, F.O. (Frank), "Armbruster Puzzles"; see http://www.armbrusterpuzzles.com/.
Grecos A. P., and R. W. Gibberd, "A Diagrammatic Solution to ‘Instant Insanity' Problem," Mathematics Magazine, 44(3): 119-124 (1971).
Peterson, Ivars, "Averting Instant
Insanity," The Mathematical Association of America,
"Puzzle inventor: Frank Armbruster," Kadon Enterprises; see http://www.gamepuzzles.com/frank.htm.
Scherphuis, Jaap, "Instant Insanity / Buvos Golyok / Drive Ya Crazy"; see http://www.geocities.com/jaapsch/puzzles/insanity.htm.
Landlands Program (1967)
Gelbart, Stephen, "An Elementary Introduction to the Langlands Program," Bulletin of the American Mathematical Society, 10(2): 177-219 (April, 1984).
Gelbart, Stephen, "Number Theory and the Langlands Program,"
International Instructional Conference: Langlands and Geometric Langlands
Program,
Mackenzie, Dana, "Fermat's Last Theorem's First Cousin," Science 287(5454): 792-793 (2000).
Mozzochi, Charles J., The Fermat Diary, (
Sprouts (1967)
Berlekamp, Elwyn R., John H. Conway, and Richard K. Guy, Winning Ways for Your Mathematical Plays (Burlington, Massachusetts: Elsevier, 1982). Originally published by Academic Press, which is now part of Elsevier.
Focardi, Riccardo and Flaminia L. Luccio, "A Modular Approach to Sprouts," Discrete Applied Mathematics, 144(3): 303–319 (2004).
Gardner, Martin, Mathematical Games: of Sprouts and Brussels Sprouts: Games with a Topological Flavor," Scientific American, 217: 112–115 (July 1967).
Lemoine, Julien and Simon Viennot, "Sprouts Wiki"; see< http://sprouts.tuxfamily.org/wiki/doku.php.
Lemoine, Julien and Simon Viennot, "A Further Computer Analysis of Sprouts"; see http://download.tuxfamily.org/sprouts/sprouts-lemoine-viennot-070407.pdf.
Peterson Ivars, "Sprouts for Spring," Science News (online), April 5, 1997, http://www.sciencenews.org/pages/sn_arc97/4_5_97/mathland.htm.
Catastrophe Theory (1968)
Darling, David, The Universal Book of Mathematics (
Casti, John, "Catastrophes, Control and the Inevitability of Spruce Budworm Outbreaks," Ecological Modeling, 14: 293-300 (1982). (On the application of catastrophe theory to insect populations.)
Gilmore, Robert, Catastrophe Theory for Scientists and Engineers (New York: Dover, 1993).
Guckenheimer, J., "The Catastrophe Controversy," Mathematical Intelligencer 1: 15-20 (1978).
Poston, Tim and Ian Stewart, Catastrophe: Theory and Its Applications (New York: Dover, 1998).
Saunders, Peter, An Introduction to Catastrophe Theory (Cambridge: Cambridge University Press, 1980).
Thom, Rene, Stabilite Structurelle et Morphogenèse, Essai d'une Theorie
Generale des Modèles. (New York: W. A. Benjamin, 1971). (Published in English as Structural
Stability and Morphogenesis: An Outline of a General Theory of Models
(D. H. Fowler, translator) (
Thom, Rene, "Topological Models in Biology," Topology 8: 313-335 (1969).
Thom, Rene, Stabilite Structurelle et Morphogenèse: Essai d'une Theorie Generale des Modèlesi (New York: Benjamin 1972).
Thom, Rene, with response by E. Christopher Zeeman, "Catastrophe Theory: Its Present State and Future Perspectives," in Dynamical Systems-Warwick 1974 (Lecture Notes in Mathematics No. 468), Anthony Manning, editor (Berlin: Springer-Verlag, 1975).
Zahler, Raphael and Sussman, Hector J., "Claims and Accomplishments of Applied Catastrophe Theory," Nature 269(10): 759-763 (1977).
Tokarsky's Unilluminable Room (1969)
Darling, David, The Universal Book of Mathematics (
Klee, Victor, "Is Every Polygonal Illuminable from Some Point?" The American Mathematical Monthly, 76(2): 180 (1969).
Stewart, Ian, "Unilluminable Rooms," Scientific American, 275(2): 100-103 (August, 1996).
Stewart, Ian, Math Hysteria (
Tokarsky, George W., "Polygonal Rooms Not Illuminable from Every Point," The American Mathematical Monthly, 102(10): 867-879 (1995).
Donald Knuth and Mastermind (1970)
♪ Mastermind was intended for sale in many different countries as evidenced by the instructions printed in 10 languages.
Bernier, J. L.,
C. Ilia Herráiz, J. J. Merelo, S. Olmeda, and A. Prieto.
"Solving Mastermind Using Gas and Simulated Annealing: A
Case of Dynamic Constraint Optimization," in Proceedings of the Fourth Conference on Parallel Problem Solving from
Nature (PPSN IV), edited
by H.-M. Voigt, W. Ebeling,
Chen, Zhixiang, Carlos Cunha, and Steven Homer, "Finding a
Hidden Code by Asking Questions," Proceedings of the Second Annual
International Conference on Computing and Combinatorics, pp. 50-55,
Knuth, Donald E., "The Computer as Master Mind," Journal of Recreational Mathematics, 9(1): 1-6 (1976-77).
Koyama, K. and Lai, T. W., "An Optimal Mastermind Strategy," Journal of Recreational Mathematics, 25(4): 251-256 (1993).
Erdos and Extreme Collaboration (1971)
Hoffman, Paul, The Man Who Loved Only Numbers (New York: Hyperion, 1999).
Schechter Bruce, My Brain Is
Open: The Mathematical Journeys of Paul Erdos (
HP-35: First Scientific Pocket Calculator (1972)
Ifrah, Georges, The Universal
History of Computing: From the Abacus to the Quantum Computer (
Lewis, Bob, "Bill
Hewlett Remembered," InfoWorld,
Waits, Bert K. and Franklin Demana, "Calculators in The Classroom: A Look To The Future" in Roles of Calculators in the Classroom (Pedro Gomez and Bert Waits, editors), electronic proceedings of Topic Group 18, International Congress on Mathematics Education, Seville, Spain; see http://ued.uniandes.edu.co/servidor/em/recinf/tg18/Waits/Waits-2.html. Also see http://ued.uniandes.edu.co/servidor/em/recinf/tg18/ArchivosPDF/Waits.pdf.
Penrose Tiles (1973)
♪ Reclusive amateur mathematician Robert Ammann (1946–1994) independently discovered these kinds of tilings at approximately the same time as Penrose. After being layed off from his programming job at the Honeywell corporation, Ammann worked as a mail sorter in a post office. Chorbachi and Loeb (see below) also discuss the occurrence of ancient indications of Penrose tilings.
According to Branko Grünbaum and G. C. Shephard, "in 1973 and 1974 Roger Penrose discovered three sets of aperiodic prototiles." For example, the first set, denoted by P1, consists of six tiles based on rhombs, regular pentagons, pentacles and ‘half-pentacles', with edges, modified by projections and indentations. The second set of aperiodic tiles, denoted by P2, "was discovered by Penrose in 1974 and is more remarkable than the first in that it contains only two tiles." The third set, denoted by P3 and consisting of two rhombs, was derived from the P2 tiling in 1974.
Chorbachi, Wasma'a K. and Arthur Loeb, "Islamic Pentagonal Seal (from Scientific Manuscripts of the Geometry of Design," in Fivefold Symmetry, Istvan Hargittai, editor (River Edge, New Jersey: World Scientific, 1992).
Gardner, Martin, Penrose Tiles to Trapdoor Ciphers (New York: W. H. Freeman and Co., 1988).
Grünbaum, Branko and G. C. Shephard, Tilings and Patterns (New York: W. H. Freeman and Co., New York 1987).
Lu, Peter, and Paul Steinhardt, "Decagonal and Quasi-Crystalline Tilings In Medieval Islamic Architecture," Science 315(5815): 1106-1110 (February, 2007).
Makovicky, Emil, "800-Year-Old Pentagonal Tiling from Maragha, Iran, and the New Varieties of Aperiodic Tiling it Inspired," in Fivefold Symmetry, Istvan Hargittai, editor (River Edge, New Jersey: World Scientific, 1992).
Penrose, Roger, "The Role of
Aesthetics in Pure and Applied Mathematical Research," Bulletin of the
Rehmeyer, Julie, "Ancient
Islamic Penrose Tiles," Science News Online, 171(8),
Senechal, Marjorie, "The Mysterious Mr. Ammann," The Mathematical Intelligencer, 26(4): 10-21 (2004).
Art Gallery Theorem (1973)
♪ Of course, if the polygon is convex, its entire interior can be viewed from any single vertex. When a polygon is concave, this is not true.
Chvátal,
Václav, "A Combinatorial Theorem in Plane Geometry," Journal of
Combinatorial Theory,
Do,
Fisk, Steve, "A Short Proof of Chvátal's Watchman Theorem," Journal of Combinatorial Theory, Series B, 24: 374 (1978).
O'Rourke, Joseph,
Rubik's Cube (1974)
♪ The Rubik's tesseract has more moves then a Rubik's Cube. In fact, if every particle in a million billion universes like ours were all Rubik's tesseracts -- and each tesseract had a different configuration for every second since the beginnings of these universes -- then these tesseracts would still not today have exhibited all possible configurations.
Hofstadter,
Kunkle, Daniel,
and Gene Cooperman, "Twenty-Six Moves Suffice for Rubik's Cube," Proceedings
of the International Symposium on Symbolic and Algebraic Computation (ISSAC
07, July 29–
"Mark Longridge's Rubik's Cube Web Site"; see http://cubeman.org/.
Munafo, Robert P., "Notable Properties of Specific Numbers" see http://home.earthlink.net/~mrob/pub/math/numbers-16.html.
Velleman, Dan, "Rubik's Tesseract," Mathematics Magazine, February 65(1): 27-36 (1992).
Chaitin's Omega (1974)
Chaitin, Gregory, "A Theory of Program Size Formally Identical to Information Theory," Association for Computing Machinery Journal, 22: 329-340 (1975). (This is the published paper in which Omega first appears. The term was used in a 1974 IBM Research Division Technical Report.)
Chaitin, Gregory, Algorithmic Information Theory, (Cambridge: Cambridge University Press, 1987).
Chaitin, Gregory, Meta Math!: The Quest
for Omega (
Chown, Marcus, "Omega Man," New
Scientist, 169(2281): 28-31 (
Darling, David, The Universal
Book of Mathematics (
Lemonick, Michael D., "It Doesn't Figure," TIME,
Gardner, Martin, "Chaitin's Omega," in Fractal Music, Hypercards and More (New York: Freeman, 1991) (Contains the writings of Charles Bennett.)
Surreal Numbers (1974)
Albers, Donald J. and G. L. Alexanderson, Mathematical People (Boston: Birkhauser, 1985).
Conway,
John, On Numbers and Games (
Knuth, Donald E., Surreal Numbers: How Two Ex-students Turned on to Pure Mathematics and Found Total Happiness (Reading, Massachusetts: Addison-Wesley, 1974).
Gardner, Martin, Mathematical Magic Show (Washington, DC: Mathematical Association of America, 1989).
Perko Knots (1974)
Perko, Kenneth A., Jr., "On the Classification of Knots," Proceedings of the American Mathematical Society, 45(2): 262-266 (August, 1974).
Haken, Wolfgang, "Theorie der Normalflachen," Acta. Math. 105: 245-375 (1961).
Pickover, Clifford, The
Mobius Strip (
Fractals (1975)
♪ Many visually interesting fractals are generated using iterative methods that were actually first introduced by mathematicians Gaston Julia (1893–1978) and Pierre Fatou (1878–1929) from 1918 to 1920. However, this field remained somewhat dormant until Benoit Mandelbrot revealed the striking beauty and intricacy of these shapes in the complex plane through the use of computer graphics.
Fatou, Pierre, "Sur les equations fonctionelles," Bulletin de la Societe Mathematique de France, 47: 161-271 (1919) and 48: 33-94, 208-314 (1920).
Julia, Gaston, "Memoire sur l'iteration des fonctions rationelles," Journal de Mathematiques Pures et Appliques, 4: 47-245 (1918).
Mandelbrot, Benoit, The Fractal Geometry of Nature (New York: W. H. Freeman, 1982).
Feigenbaum Constant (1975)
Feigenbaum, Mitchell, "Computer Generated Physics," in Twentieth Century Physics, edited by Laurie M. Brown, Abraham Pais, and Brian Pippard (New York: American Institute of Physics Press, 1995), 1823-1853.
May, Robert, "Simple mathematical models with very complicated dynamics," Nature, 261: 459-567 (1976).
Public-Key Cryptography (1977)
Diffie, Whitfield and Hellman, Martin, "New Directions in Cryptography," IEEE Transactions on Information Theory, 22(6): 644-654 (1976).
Hellman, Martin, "The Mathematics of Public-Key Cryptography," Scientific American, 241(2): 146-157 (August, 1979).
Lerner, K. Lee, and Brenda Wilmoth Lerner, editors, Encyclopedia of Espionage Intelligence and Security (Farmington Hills, Michigan, Gale Group, 2004). On the Web, visit "Intelligence Encyclopedia information about World War I: Loss of the German Codebook," Encyclopedia of Espionage, Intelligence, and Security; see http://www.answers.com/topic/world-war-i-loss-of-the-german-codebook.
Rivest, Ronald, Shamir, Adi, and Adleman, Leonard, "A Method for Obtaining Digital Signatures and Public Key Cryptosystems," Communications of the ACM, 21(2): 120-126 (February, 1978).
Szilassi Polyhedron (1977)
Peterson, Ivars, "A Polyhedron with a Hole," Science News
Online, 71(3),
Szilassi, Lajos, "Regular Toroids," Structural Topology, 13: 69-80 (1986).
Ikeda Attractor (1979)
Ikeda, Kensuke, "
Ikeda, Kensuke, H. Daido, and O. Akimoto, "Optical Turbulence: Chaotic Behavior of Transmitted Light from a Ring Cavity," Physical Review Letters, 45, 709-712 (1981).
Pickover, Clifford, A Passion
for Mathematics (
Strogatz, Steven H., Nonlinear Dynamics
and Chaos: With Applications to Physics, Biology, Chemistry and Engineering
(
Spidrons (1979)
Erdely, Dániel, "Official Spidron Page"; see http://www.spidron.hu/.
Peterson, Ivars, "Swirling Seas, Crystal Balls, Spirals of
Triangles Crinkle into Intricate Structures," Science News, 170(17): 266
(
Mandelbrot Set (1980)
♪ The Mandelbrot set plays an important role in complex dynamics, a field that had its beginnings in the work of French mathematicians Pierre Fatou (1878–1929) and Gaston Julia (1893–1978) in the early 1900s.
Brooks, Robert and Peter Matelski, "The dynamics of
2-generator subgroups of PSL(2,C)," in Riemann
Surfaces and Related Topics: Proceedings of the 1978 Stony Brook Conference,
Kyra,
Clarke, Arthur, C., The Ghost
From the
Darling, David, The Universal
Book of Mathematics (
Fatou, Pierre, "Sur les equations fonctionelles, " Bulletin de la Societe Mathematique de France, 47: 161-271 (1919) and 48: 33-94, 208-314 (1920).
Julia, Gaston, "Memoire sur l'iteration des fonctions rationelles," Journal de Mathematiques Pures et Appliques, 4: 47-245 (1918).
Mandelbrot, Benoit, "Fractal aspects of the iteration of z →λz(1 - z) for complex λ and z," Annals of the New York Academy of Sciences, 357: 249-259 (1980).
Mandelbrot, Benoit, The Fractal Geometry of Nature (New York: W. H. Freeman, 1982).
Wegner, Tim and Peterson, Mark, Fractal Creations (Corte Madera, California: Waite Group Press, 1991).
Monster Group (1981)
Conway, John H. and Sloane, N. J. A., "The Monster Group and its 196884- Dimensional Space" and "A Monster Lie Algebra?" Chapters 29-30 in Sphere Packings Lattices, and Groups, 2nd edition (New York: Springer-Verlag, 1993), pp. 554-571.
Griess, Robert L., Jr, "The Friendly Giant," Inventiones Mathematicae 69(1): 1-102 (1982).
Griess, Robert L., Jr., Ulrich Meierfrankenfeld, and Yoav Segev, "A Uniqueness Proof for the Monster," The Annals of Mathematics, 2nd Ser., 130(3): 567-602 (November, 1989).
Ronan, Mark, Symmetry
and the Monster: The Story of One of the Greatest Quests of Mathematics (
Ball Triangle Picking (1982)
Buchta, Christian, "A Note on the Volume of a Random
Polytope in a Tetrahedron,"
Eisenberg, Bennett and Rosemary Sullivan, "Crofton's Differential Equation," The American Mathematical Monthly, 107(2): 129-139 (2000).
Hall, Glen R., "Acute Triangles in the n-Ball," Journal of Applied Probability. 19: 712-715 (1982).
Weisstein, Eric W., "Ball Triangle Picking,"" From MathWorld--A Wolfram Web Resource; see http://mathworld.wolfram.com/BallTrianglePicking.html.
Jones Polynomial (1984)
♪ The HOMFLY polynomial got its name from the last names of its co-discoverers: Hoste, Ocneanu, Millett, Freyd, Lickorish, and Yetter. Independent work related to the HOMFLY polynomial was conducted by Prztycki and Traczyk.
Adams, Colin Conrad, The Knot Book: An Elementary Introduction
to the Mathematical Theory of Knots (
Devlin, Keith J., The Language of Mathematics: Making the
Invisible Visible (
Freyd, P., Yetter, D., Hoste, J., Lickorish, W. B. R., Millett, K., and Oceanu, A., "A New Polynomial Invariant of Knots and Links," Bulletin of the American Mathematical Society, 12(2): 239-246 (1985).
Jones, Vaughan, "A Polynomial Invariant for Knots via von Neumann Algebras," Bulletin of the American Mathematical Society, 12: 103-111 (1985).
Przytycki, Józef and Traczyk, Pawel,
"
Weeks Manifold (1985)
Cipra, Barry, "In Hyperbolic
Space, Size Matters," Science 317(5834): 38 (
Gabai, David, Robert Meyerhoff, and Peter Milley, "Minimum Volume Cusped Hyperbolic Three-Manifolds," arXiv preprint at http://front.math.ucdavis.edu/0705.4325.
Weeks, Jeffrey, Hyperbolic Structures
on 3-Manifolds,
Weeks, Jeffrey, The
Shape of Space: How to Visualize Surfaces and Three-Dimensional Manifolds,
Second Edition (
Andrica's Conjecture (1985)
♪ Andrica writes in his 2005 paper, "I discovered this problem in the period 1976-1981 when I have been extremely interested in prime number theory. The conjecture was first time published in the note of 1985 [see below]. In 1985, I have communicated the problem to Richard Guy, at that time editor to the section about open problems of journal The American Mathematical Monthly."
Andrica, Dorin, "About a Conjecture on Prime Number Theory"
(Romanian), Revista
Matematică a Elevilor din
Andrica, Dorin, "Note on a Conjecture in Prime Number
Theory,"
Andrica, Dorin, "On a Conjecture in Prime Number Theory," Proceedings
of the
Guy, Richard., Unsolved Problems in Number Theory, Second Edition (New York: Springer, 1994), Third Edition, 2005.
The ABC Conjecture (1985)
Darling, David, The Universal
Book of Mathematics (
Goldfeld, Dorian, "Beyond the Last Theorem," Math Horizons, pp. 26-34 (September, 1996).
Goldfeld, Dorian, "Beyond the Last Theorem," The Sciences, pp. 34-40 (March/April 1996).
Masser, David W., "On a b c and Discriminants," Proc. Amer. Math. Soc., 130: 3141-3150 (2002).
Nitaq, Abderrahmane, "The abc Conjecture Home Page," Departement de Mathematiques, Universite de Caen, France; see http://www.math.unicaen.fr/~nitaj/abc.html.
Oesterle, Joseph, "Nouvelles approches du 'theorème' de Fermat," Asterisque 161/162: 165-186 (1988).
Peterson, Ivars, "MathTrek: The Amazing ABC Conjecture," Mathematical
Association of
Audioactive Sequence (1986)
♪
x71 − x69 − 2x68 − x67 + 2x66 + 2x65 + x64 − x63 − x62 − x61 − x60 − x59 +
2x58 + 5x57 + 3x56 − 2x55 − 10x54 − 3x53 − 2x52 + 6x51 + 6x50 + x49 + 9x48 − 3x47 −
7x46 − 8x45 − 8x44 + 10x43 + 6x42 + 8x41 − 5x40 − 12x39 + 7x38 − 7x37 + 7x36 + x35 −
3x34 + 10x33 + x32 − 6x31 − 2x30 − 10x29 − 3x28 + 2x27 + 9x26 − 3x25 + 14x24 − 8x23 −
7x21 + 9x20 + 3x19 − 4x18 − 10x17 − 7x16 + 12x15 + 7x14 + 2x13 − 12x12 − 4x11 −
2x10 + 5x9 + x7 − 7x6 + 7x5 − 4x4 + 12x3 − 6x2 + 3x − 6.
Conway, John, "The Weird and Wonderful Chemistry of
Audioactive Decay,"
Conway, John, "The Weird and Wonderful Chemistry of Audioactive Decay," in Open Problems in Communication and Computation, T. M. Cover and B. Gopinath, editors, (New York: Springer, 1987), pp. 173–188.
Conway, John H. and Guy, Richard. K., "The Look and Say Sequence," in The Book of Numbers (New York: Copernicus/Springer, 1996).
Hilgemeir, Mario, "Die Gleichniszahlen-Reihe," Bild der Wissenschaft, 12: 194-195 (1986).
Hilgemeir, Mario, "One Metaphor Fits All: A Fractal Voyage with
Lakhtakia, Akhlesh and Pickover, Clifford, "Observations on the Gleichniszahlen-Reihe, an Unusual Number Theory Sequence," Journal of Recreational Mathematics. 25(3): 202-205 (1993).
Pickover, Clifford and Khorasani, Elahe, "Visualization of the Gleichniszahlen-Reihe, an Unusual Number Theory Sequence," Mathematical Spectrum, 23(4): 113-115 (1991).
Pickover, Clifford, Chaos in Wonderland (New York: St. Martin's Press, 1994). (Mentions the work of Roger Hargrave.)
Pickover, Clifford, "Audioactive Decay," Chapter 55 in Wonders
of Numbers: Adventures in Mathematics, Mind, and Meaning (
Mathematica (1988)
♪ Mathematica is a trademark of Wolfram Research, Inc. Maple is a trademark of Waterloo Maple, Inc. Mathcad is a trademark of Mathsoft, Inc. MATLAB is a trademark of The MathWorks, Inc.
Berlinski, David, "Ground Zero: A Review of the Pleasures of Counting, by T. W. Koerner," The Sciences, July/August 1997, pp. 37-41.
Borwein, Jonathan and David H.
Bailey, Mathematics by Experiment: Plausible Reasoning in the 21st Century (
"About Mathematica"; see http://www.stephenwolfram.com/about-mathematica/.
"Wolfram Research"; see http://www.wolfram.com/.
"Open Directory: Science and Math Software"; see http://www.dmoz.org/Science/Math/Software/.
Murphy's Law and Knots (1988)
Deibler, Richard W., Jennifer K. Mann, De Witt L. Sumners, and Lynn Zechiedrich, "Hin-Mediated DNA Knotting and Recombining Promote Replicon Dysfunction and Mutation," BMC Molecular Biology, 8: 44 (2007). (This paper suggests that DNA knotting can be very bad for the cell, promoting replication dysfunction and high rates of mutation in bacteria.)
Matthews, Robert A. J., "Knotted Rope: A Topological Example of Murphy's Law," Mathematics Today 33: 82-84 (July-August, 1997);
see http://ourworld.compuserve.com/homepages/rajm/knotfull.htm.
Peterson, Ivars, "Knotted Walks," Science News Online,
Peterson, Ivars, "Knots in Proteins," Science News Online,
170(16),
Raymer, Dorian M. and Douglas E. Smith, "Spontaneous knotting of an agitated string," Proceedings of the National Academy of Sciences USA, 104(2): 16432-16437 (October, 2007).
Sumners, De Witt L. and Stuart G. Whittington, "Knots in Self-avoiding Walks," Journal of Physics A 21:1689–1694 (1988).
Taylor, William and Kuang Li, "Protein knots—A tangled problem," Nature 421: 25 (2003).
Taylor, William, "A Deeply Knotted Protein Structure and How it Might Fold," Nature, 406: 916-919 (2000).
Virnau, Peter, Leonid A. Mirny, and Mehran Kardar, "Intricate Knots in Proteins: Function and Evolution," PLoS Computational Biology, 2(9): 1074-1059 (September, 2006).
Butterfly Curve (1989)
♪
Fay actually created the Butterfly Curve while at the
Fay,
The On-Line Encyclopedia of Integer Sequences (1996)
Sloane, Neil, A Handbook of Integer Sequences (San Diego, California: Academic Press, 1973), originally published by Academic Press, which is now part of Elsevier.
Sloane, Neil and Simon Plouffe, The Encyclopedia of Integer Sequences (San Diego, California: Academic Press, 1995).
Sloane, Neil, "The On-Line Encyclopedia of Integer Sequences"; see http://www.research.att.com/~njas/sequences/.
Sloane, Neil, "My Favorite Integer Sequences," in Sequences and their Applications, in edited by Ding, C., T. Helleseth, and H. Niederreiter (London: Springer-Verlag, 1999), arXiv:math/0207175.
Sloane, Neil, "The On-Line Encyclopedia of Integer Sequences," Notices of the American Mathematical Society 50(8): 912–915 (2003); see http://www.ams.org/notices/200308/comm-sloane.pdf.
Stephan, Ralf, "Prove or Disprove: 100 Conjectures from the OEIS," 2004; see http://arxiv.org/abs/math.CO/0409509.
Eternity Puzzle (1999)
Selby, Alex, "Eternity Solution"; see http://www.archduke.demon.co.uk/eternity/solution/.
Weisstein, Eric W., "Eternity," from MathWorld--A Wolfram Web Resource; see http://mathworld.wolfram.com/Eternity.html.
Perfect Magic Tesseract (1999)
♪ When we talk about broken diagonals of a magic square, we refer to the diagonals that leave one end of the square and return along another. For a perfect magic cube, the numbers are arranged so that each row, each column, each main diagonal of the square cross sections, and each of the four great (space) diagonals (sometimes called "triagonals") containing N integers will add to the same sum.
John Hendricks was one of the world's foremost experts on higher-dimensional magic objects, and, for example, he computed third-order magic tesseracts in which the 27 rows, 27 columns, 27 pillars, and 27 files sum to 123. Quadragonals join opposite corners, and the numbers along the quadragonals must all sum to the magic sum. Because the object has 16 corners, 8 quadragonals exist.
Hendricks, John, "The Five-and Six-dimensional Magic Hypercubes of Order 3," Canadian Mathematical Bulletin, May, 5(2): 171-189 (1962).
Hendricks, John, "The Magic Tesseracts of Order 3 Complete," Journal of Recreational Mathematics, 22(1): 16-26 (1990).
Henricks, John, "Magic Tesseract," in The Pattern Book: Fractals, Art, and Nature. Pickover, Clifford, Editor (River Edge, New Jersey: World Scientific, 1995).
Pickover, Clifford, The Zen
of Magic Squares, Circles, and Stars (
Parrondo's Paradox (1999)
♪ Note that in game A or game B played separately, you are guaranteed to lose in the long run for any allowed value of x up to 0.1.
Blakeslee, Sandra, "Paradox in Game Theory: Losing Strategy
That Wins," The
Harmer, Gregory P. and Derek Abbott, "Game theory: Losing Strategies Can Win by Parrondo's Paradox," Nature 402: 864 (1999).
Harmer, Gregory P. and Derek Abbott, "Parrondo's Paradox," Statistical Science, 14(2): 206-213 (1999).
Harmer, Gregory P., Derek Abbott, Peter G. Taylor, "The Paradox of Parrondo's Games," Proceedings: Mathematical, Physical and Engineering Sciences, 456(1994): 247-259 (February, 2000).
"The Official Parrondo's Paradox Page," The University of Adelaide; see http://www.eleceng.adelaide.edu.au/Groups/parrondo/
Solving of the Holyhedron (1999)
Hatch, Don, "Holyhedron"; see http://www.plunk.org/~hatch/Holyhedron/.
Vinson, Jade, "On Holyhedra," Discrete and Computational Geometry, 24(1): 85-104 (2000).
Bed Sheet Problem (2001)
"Folding Paper in Half 12 Times," The Historical Society of Pomona Valley; see http://www.pomonahistorical.org/12times.htm.
Kruszelnicki, Karl S., "Folding Paper: Great Moments in Science"; see http://www.abc.net.au/science/k2/moments/s1523497.htm.
Peterson, Ivars, "Folding Paper in
Half—Twelve Times," Science News Online, Week of. 165(4),
Weisstein, Eric W., "Folding," from MathWorld--A Wolfram Web Resource; see http://mathworld.wolfram.com/Folding.html.
Wong, Willie W., "Folding Paper: Beyond Conventional Wisdom," see http://www.math.princeton.edu/~wwong/blog/blog200511170411.shtml.
Solving the Game of Awari (2002)
Peterson, Ivars, "Solving an Ancient African Game," The
Mathematical Association of
Romein, John W. and Henri E. Bal, "Solving the Game of Awari using Parallel Retrograde Analysis," IEEE Computer, 36(10): 26-33 (October 2003).
Tetris is NP-Complete (2002)
♪ The scoring formula for most of the Tetris products takes into account the fact that certain row clearing operations are more difficult than others and thus should be awarded more points. Some games also award points based on the height the piece fell before locking.
Breukelaar, Ron, Erik D. Demaine, Susan Hohenberger, Hendrik Jan Hoogeboom, Walter A. Kosters, and David Liben-Nowell, "Tetris is Hard, Even to Approximate," International Journal of Computational Geometry and Applications, 14(1): 41-68 (April 2004).
Demaine, Erik D., Susan Hohenberger, and David Liben-Nowell, "Tetris is Hard, Even to Approximate," Computing and Combinatorics, 9th Annual International Conference, T. Warnow, and B. Zhu (editors), Lecture Notes in Computer Science 2697, pp. 351-363 (2003).
Peterson, Ivars, "Tetris Is Hard,"
The Mathematical Association of America,
NUMB3RS (2005)
♪ Interestingly, real-life crime cases often hinge on mathematics. For example, in 2005, the Pythagorean Theorem played a crucial role in a case before the New York State Court of Appeals, in which a man was convicted of selling drugs within 1,000 feet of a school. The Court decided that the length of the hypotenuse and not the leg lengths (corresponding to the actual streets the man could walk) should be used when determining the distance.
Devlin, Keith and Gary Lorden, The Numbers Behind
NUMB3RS: Solving Crime with Mathematics (
Devlin, Keith, "NUMB3RS Gets the Math Right," The Mathematical Association of America, February, 2005; see http://www.maa.org/devlin/devlin_02_05.html.
Frazier, Kendrick, "Do They Have Your Numb3r?", Skeptical Inquirer, January/February, 2007; see http://www.csicop.org/si/2007-01/numb3r.html.
Peterson, Ivars, "Geometry in
Court," Science News Online, 170(22),
"Press Release 07-040: The ‘Numb3rs' Add Up: Popular TV Show and Its Creators Receive Public Service Award," The National Science Foundation; see http://www.nsf.gov/news/news_summ.jsp?cntn_id=108701.
Weisstein, Eric, "The Math(ematica) behind Television's
Crime Drama NUMB3RS,"
Checkers is Solved (2007)
Cho,
Schaeffer, Jonathan, One Jump Ahead: Challenging Human Supremacy in Checkers. (New York: Springer-Verlag, 1997).
Schaeffer, Jonathan, Neil Burch, Yngvi Bjornsson, Akihiro Kishimoto, Martin Müller, Robert Lake, Paul Lu, and Steve Sutphen, "Checkers Is Solved," Science, 317(5844): 1518-1522 (September 14, 2007), published online, July 19, 2007 at http://www.sciencemag.org/cgi/content/abstract/1144079.
The Quest for Lie Group E8 (2007)
♪ Also in 2007, physicist A. Garrett Lisi speculated that E8 explained how the various fundamental particles in physics may result from different aspects of the strange and beautiful symmetries of E8. In particular, he found a way to place the various elementary particles and forces on the 248 points of E8. Twenty gaps remained, which he populated with "notional particles," such as those predicted to be associated with gravity. It is possible that Lisi's highly speculative theory, or similar theories, are complementary to string theory rather than an alternative to string theory.
In 2008, Scientific American featured a news story skeptical of Lisi's E8 theory; nonetheless, it is fascinating the degree to which mathematics is used to explore the fabric of reality. Albert Einstein once remarked that he sought truth in equations and then trusted that experiments would one day verify his theories. "Our experience hitherto justifies us in believing that nature is the realization of the simplest conceivable mathematical ideas," Einstein wrote. "I am convinced that we can discover by means of purely mathematical constructions the concepts and laws connect them with each other."
Collins, Graham, "Wipeout? A Hyped Theory of Everything Sinks from Sight," Scientific American, 298(4): 30-33 (April 2008).
Lisi, A. Garrett, "An
Exceptionally Simple Theory of Everything," submitted on
Mackenzie, Dana, "Mathematics: Mapping the
Merali, Zeeya, "Is Mathematical Pattern
the Theory of Everything?" New Scientist, 196(2630): 8-10 (
"Mathematicians Map E8," The American Institute of Mathematics; see http://aimath.org/E8/.
Mathematical Universe Hypothesis (2007)
♪ Tegmark's theory was partly based on a talk given at the symposium "Multiverse and
String
Theory: Toward Ultimate Explanations in Cosmology" held on
The theorist A. Garrett Lisi speculates in Zeeya Merali's "Is Mathematical Pattern the Theory of Everything?": "I think the universe is pure geometry -- basically, a beautiful shape twisting around and dancing over space-time. Since E8 [a complex, eight-dimensional mathematical pattern with 248 points] is perhaps the most beautiful structure in mathematics, it is very satisfying that nature appears to have chosen this geometry."
To my mind, mathematics is a process of discovery. Mathematicians are like archeologists. Physicist Roger Penrose felt the same way about fractal geometry. In his book The Emperor's New Mind, he says that fractals (for example, intricate patterns such as the Julia set or Mandelbrot set) are out there waiting to be found:
"It would seem that the Mandelbrot set is not just part of our
minds, but it has a reality of its own...
The computer is being used in essentially the same way that an experimental
physicist uses a piece of experimental apparatus to explore the structure of
the physical world. The Mandelbrot set
is not an invention of the human mind:
it was a discovery. Like
Collins, Graham, "Wipeout? A Hyped Theory of Everything Sinks from Sight," Scientific American, 298(4): 30-33 (April 2008).
Egan,
Greg,
Fredkin, Edward, "Five Big Questions with Pretty Simple Answers, IBM Journal of Research and Development, 48(1): 31-35 (January, 2004).
Lisi, A. Garrett, "An
Exceptionally Simple Theory of Everything," submitted on
Fredkin, Edward, "Digital Mechanics," Physica D 45: 254 –270 (1990).
Tegmark, Max, "Is ‘The Theory of Everything' Merely the Ultimate Ensemble Theory?" Annals of Physics, 270(1): 1-51 (1998).
Merali, Zeeya, "Is Mathematical Pattern
the Theory of Everything?" New Scientist, 196(2630): 8-10 (
Tegmark,
Max, "Mathematical Cosmos: Reality by Numbers," New Scientist,
195(2621): 39-41 (
Tegmark, Max, "The Mathematical
Universe,"
Tegmark, Max, "Shut up and Calculate,"
Tegmark, Max, "Multiverse and String Theory," in Visions
of Discovery: Shedding New Light on Physics and Cosmology, edited by R. Y.
Chiao, M. L. Cohen, A. J. Leggett, W. D. Phillips, and C. L. Harper, Jr. (
Penrose, Roger, The Emperor's New Mind (New York: Penguin, 1991).
Pickover, Clifford, A Passion
for Mathematics (
Pickover, Clifford, A Beginner's Guide to Immortality: Extraordinary
People, Alien Brains, and Quantum Resurrection (
Rucker, Rudy, The Lifebox, the Seashell, and the Soul
(
Schmidhuber, Jürgen, "A Computer Scientist's View of Life, the Universe, and Everything," in Foundations of Computer Science: Potential - Theory - Cognition, Lecture Notes in Computer Science, edited by Freksa, C., Jantzen, M., and Valk, R. (New York, Springer, 1997), pp. 201-208; see http://www.idsia.ch/~juergen/computeruniverse.html.
Wigner,
Wolfram,
Stephen, A New Kind of Science (
Zuse, Konrad, "Rechnender Raum" ("Calculating Space"), Elektronische Datenverarbeitung, 8: 336-344 (1967).
 Konrad Zuse published one of the first works on digital physics that proposed that the
universe is being computed on a discrete "device." (See reference above)
Konrad Zuse published one of the first works on digital physics that proposed that the
universe is being computed on a discrete "device." (See reference above)