Hamiltonian Chaos
Chaos and Time-Series Analysis
10/24/00 Lecture #8 in Physics 505
This is probably the most technically difficult
lecture of the course.
 Comments on Homework
#6 (Lyapunov Exponent)
Comments on Homework
#6 (Lyapunov Exponent)
-
Not everyone had a good graph of LE versus
C
for B = 0.3
-
Some had numerical troubles with unbounded orbits (C > 1.42)
-
BASIC code for doing part 3 has been put
on the WWW
 Review (last
week) - Bifurcations
Review (last
week) - Bifurcations
-
Bifurcation is a qualitative change in behavior at a critical
parameter value
-
Observation of a bifurcation verifies determinism
-
Flows are often analyzed using their maps (Poincaré
section)
-
Classifications:
-
Local - involves single equilibrium points
-
Global - equilibrium points appear or vanish
-
Continuous (subtle) - eigenvalues cross unit circle
-
Discontinuous (catastrophic) - eigenvalues appear or vanish
-
Explosive - like catastrophic but no hysteresis
(occur when attractor touches the basin boundary)
-
There are dozens of bifurcations, many not discovered
-
Terminology is not precise or universal (still evolving)
-
Transcritical Bifurcation
-
Pitchfork Bifurcation
-
Flip Bifurcation
-
Tangent (or Saddle-Node or Blue Sky) Bifurcation
-
Catastrophe (1-D example)
-
Hopf Bifurcation
-
Niemark (or Secondary Hopf) Bifurcation
-
A stable limit cycle becomes unstable and a 2-torus is born
-
The Poincaré section exhibits a Hopf bifurcation
-
Main sequence (quasi-periodic route to chaos)
-
fixed point --> limit cycle --> 2-torus --> chaos
-
N-torus with N > 2 not usually seen (Piexito's Theorem)
(3-torus and higher are structurally unstable)
-
This contradicts the Landau theory of turbulence
(turbulence is a sum of very many periodic modes)
-
Also called the Newhouse-Ruelle-Takens route
-
Probably the most common route to chaos at high-D
 Hamiltonian Systems -
Introduction and Motivation
Hamiltonian Systems -
Introduction and Motivation
-
These are systems that conserve mechanical energy
-
They have no dissipation (frictionless)
-
They are of historical interest and importance
-
Examples (all from physics):
-
Planetary motion (recall 3-body problem)
-
Charged particles in magnetic fields
-
Incompressible fluid flows (liquids)
-
Trajectories of magnetic field lines
-
Quantum mechanics
-
Statistical mechanics
 A Case Study - Mass on
a Spring (frictionless)
A Case Study - Mass on
a Spring (frictionless)
-
dx/dt = v
-
dv/dt = -(k/m)x
-
This system has 1 spatial dimension (1 degree of freedom)
-
It has a 2-D phase space however
-
Solution: kx2 + mv2 =
constant (conservation of energy)
-
Hamiltonian: H = kx2/2 + mv2/2
(total energy)
-
kx2/2 is the potential energy (stored in spring)
-
mv2/2 is the kinetic energy (energy of motion)
-
Let k = m = 1 for simplicity
-
Given the Hamiltonian, we can get the equations of motion:
-
dx/dt = dH/dv
= v
-
dv/dt = -dH/dx
= -x
-
where d is the partial derivative
-
The motion occurs along a 1-D curve in 2-D space
-
This curve is not a limit cycle (it is a center)
-
Such a system cannot exhibit chaos (even if driven)
 Hamilton's Equations
(N Dimensions)
Hamilton's Equations
(N Dimensions)
-
Generalize the above ideas to dimensions N > 1:
-
dqi/dt = dH/dpi
(q is a generalized coordinate)
-
dpi/dt = -dH/dqi
(p is a generalized momentum = mv)
-
p and q constitute the phase space for
the dynamics
-
N-dimensional dynamics have a 2N-dimensional phase space
-
pi and qi (for i
= 1 to N) are the phase space variables
-
Note: dH/dt = dH/dp
dp/dt + dH/dq
dq/dt = 0
-
H is a constant of the motion (Hamiltonian)
-
There may be other constants (say a total of k)
-
The dynamics are constrained to a 2N - k dimensional
space
-
Hamiltonian's equations are just another dynamical ODE system:
-
dq/dt = f(p, q)
-
dp/dt = g(p, q)
-
...
-
Note: dV/dt / V = trace J = fq
+ gp + ...
= d/dq
[dH/dp]
+ d/dp
[-dH/dq]
+ ... = 0
-
Phase-space volume is conserved
 Properties of Hamiltonian
Systems
Properties of Hamiltonian
Systems
-
They have no dissipation (frictionless)
-
There are one or more conserved quantities (energy, ...)
-
They are described by a Hamiltonian function H
-
There are 2N dimensions for N degrees of freedom
-
Motion is on a 2N - k dimensional (hyper)surface
-
k + 1 Lyapunov exponents are equal to zero
-
There are no attractors (or attractor = basin)
-
Transients don't die away (no need to wait)
-
Equations are time-reversible
-
Orbit returns arbitrarily close to the initial condition
-
Phase-space volume is conserved (Liouville's theorem)
-
The flow is incompressible (like water)
-
The Lyapunov exponents sum to zero
-
Chaos can occur only for N > 1 (at least 2 degrees
of freedom)
-
The dynamics occur in a space of integer dimension
-
This space may be a (fat)
fractal however (many holes)
 2-D Symplectic (Area-Preserving)
Maps
2-D Symplectic (Area-Preserving)
Maps
-
Xn+1 = f(Xn, Yn)
-
Yn+1 = g(Xn, Yn)
-
An+1/An = |det J|
= |fxgy - fygx|
= 1
-
Example: Hénon map with B = 1
-
Xn+1 = 1 - CXn2
+ Yn
-
Yn+1 = Xn
-
An+1/An = |0 - (1)(1)| =
1
-
Computer demo (C = 0.3)
-
More general polynomial symplectic map:
-
Xn+1 = A + Yn + F(Xn)
-
Yn+1 = B - Xn
-
One choice of F is C1 + C2X
+ C3X2 + ...
-
Verify that this has An+1/An
= |det J| = 1
-
Slide show from Strange
Attractors book
-
Stochastic web maps:
-
These occur for charged particle in EM wave
-
Xn+1 = a1 + [Xn
+ a2sin(a3Yn + a4)]cos
a
+ Ynsin a
-
Yn+1 = a5 + [Xn
+ a2sin(a3Yn + a4)]sin
a
+ Yncos a
-
where a = 2p/N
(N is an integer)
-
Verify that this has An+1/An
= |det J| = 1
-
l1 is positive but small
-
Exhibit minimal chaos or Arnol'd diffusion
-
Examples: case 1
(N = 9) / case 2 (N
= 5)
 Simple Pendulum (2-D
Conservative Flow)
Simple Pendulum (2-D
Conservative Flow)
-
dx/dt = v (v is really an angular
velocity)
-
dv/dt = -sin x (x is really an
angle)
-
For x << 1, sin x --> x and orbits
are circles around a center:
-
More generally equilibria are at v* = 0, x* = Np
(where N is an integer, N = 0, ±1, ±2,
±3, ...)
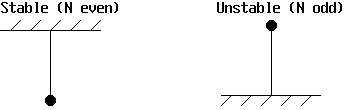
-
Phase space trajectories:
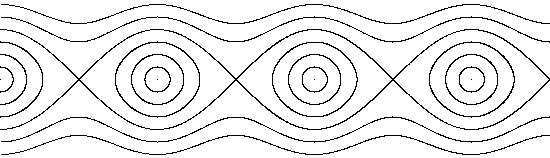
-
O-points (centers) and X-points (saddle points)
-
Separatrix (homoclinic orbit) separates trapped (elliptic)
and passing (hyperbolic) orbits
-
Homoclinic orbits are sensitive to perturbations
 Chirikov (Standard) Map
Chirikov (Standard) Map
-
Start with the pendulum equations:
-
Solve by the leap-frog method:
-
vn+1 = vn - h1sin
xn
-
xn+1 = xn + h2vn+1
-
Leap frog is symplectic if fx = gv
= 0
-
Let q = x/2p,
r = v/2p, h1
= K, h2 = 1:
-
2prn+1 = 2prn
- K sin(2pqn)
-
2pqn+1 = 2pqn
+ 2prn+1
-
rn+1 = [rn - (K/2p)
sin(2pqn)] mod 1
-
qn+1 = [qn
+ rn+1] mod 1
-
K is the nonlinearity parameter
-
This system also models ball bouncing on vibrating floor
-
Animation of Chirikov
map

J. C. Sprott | Physics 505
Home Page | Previous Lecture | Next
Lecture