Bifurcations

Comments on Homework #5 (Hénon Map)

• Everyone did fine
• Many noted the large number of iterates required when zoming in on the attractor
• Only a couple of people had a good plot of the basin of attraction

Review (last week) - Strange Attractors

• Kaplan-Yorke (Lyapunov) Dimension
• D_KY = D - (l₁ + l₂ + ... + l_D) / l_D+1
• where D is the largest integer for which l₁ + l₂ + ... + l_D > 0
• D_KY = 1.258 for Hénon map (B = 0.3, C = 1.4)
• D_KY = 2.062 for Lorenz attractor (p = 10, r = 28, b = 8/3)
• Chaotic flows always have D_KY > 2
• Hence we need visualization techniques
• Chaotic maps always have D_KY  > 1
• Why not use a multipoint interpolation?
• Is chaos the rule or the exception?
• Polynomial maps and flows
• Artificial neural networks
• Examples of strange attractors
• Properties of strange attractors
• Dimension of strange attractors
• Strange attractors as general approximators
• Strange attractors as objects of art

What is the "Most Chaotic" 2-D Quadratic Map?

• This work is unpublished
• Use genetic algorithm to maximize l₁ for 12 parameters
• Mate 2 chaotic cases (arbitrarily chosen)
• Kill inferior offspring (eugenics)
• Introduce occasional mutations
• Replace parents with superior children
• The answer?  - 2 decoupled logistic maps!
• X_n+1 = 4X_n(1 - X_n)
• Y_n+1 = 4Y_n(1 - Y_n)
• This system has l₁ = l₂ = log(2) as expected
• It is area expanding but folded in both directions
• Its Kaplan-Yorke dimension is D_KY = 2
• Largest Lyapunov exponent generally decreases with D
• Implications
• Complex systems evolve at the "edge of chaos"
• Allows exploration of new regions of state space
• But retains good short-term memory

Shift Map (1-D Nonlinear)

• Start with logistic map:  X_n+1 = 4X_n(1 - X_n)
• Let  X = sin² pY
• Then  sin² pY_n+1 = 4 sin² pY_n (1 - sin² pY_n)

= 4 sin² pY_n cos² pY_n
• But  2 sin q cos q = sin 2q  (from trigonometry)
• Hence  sin² pY_n+1 = sin² 2pY_n
• Thus  Y_n+1 = 2Y_n (mod 1)  (shift map)
• "mod 1" means take only the fractional part of 2Y_n
• Caution:  mod only works for integers on some compilers

In this case, use instead:
IF X >= 1 THEN X = X - INT(X)
IF X < 0 THEN X = INT(X) - X
• Shift map is conjugate to the logistic map

(equivalent except for a nonlinear change of variables)
• More specifically, this is a piece-wise linear map
• Maps the unit interval (0, 1) back onto itself twice:


• Involves a stretching and tearing
• Lyapunov exponent:  l = log(2)
• Invariant measure (probability density) is uniform
• Generates apparently random numbers in (0, 1)
• But these numbers are strongly correlated (obviously)
• Solution:  Y_n = 2ⁿY₀ mod 1
• Why is it called a "shift map"?
• Represent initial condition in binary:  0.1011010011...
• Or in (left/right) symbols:  RLRRLRLLRR...
• Each iteration left-shifts by 1:  1.011010011...
• Mod 1 discards the leading 1:  0.011010011...
• The sequence is determined by the initial condition
• Only irrational initial conditions give chaos
• Any sequence of RL's can be generated
• Computer hint:  Use  X_n+1 = 1.999999X_n mod 1
• Dynamics are similar in the tent map:

Computer Random Number Generators

• A generalization of the shift map:  Y_n+1 = (AY_n + B) mod C
• A, B, and C must be chosen optimally (large integers)
• A is the number of cycles
• B is the "phase" (horizontal shift)
• C is the number of distinct values
• Example:  A = 1366, B = 150889, C = 714025
• There are many other choices (see Knuth)
• Must also choose an initial "seed" Y₀
• This is called a "linear congruential generator"


• Lyapunov exponent:  l = log(A)  (very large)
• Numbers produced this way are pseudo-random
• The sequence will repeat after at most C steps
• In QuickBASIC the numbers repeat after 16,777,216 = 2¹⁴ steps
• The repetition time is much longer in PowerBASIC
• Cycle time can be increased with shuffling

Intermittency - Logistic Map at A = 3.8284

• This is just to the left of the period-3 window
• Dynamics change abruptly from period-3 to chaos
• Time series (X_n versus n):


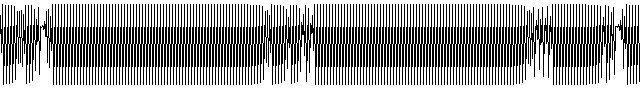
• This is a result of a tangent bifurcation(X_n+3 versus X_n)
• Can be understood by the cobweb diagram
• Orbit gets caught for many iterations in a narrow channel
• This is the intermittency route to chaos  (cf: transient chaos)

Bifurcations - General

• A qualitative change in behavior at a critical parameter value
• Observation of a bifurcation verifies determinism
• Flows are often analyzed using their maps (Poincaré section)
• Classifications:
• Local - involves one or more equilibrium points
• Global - equilibrium points appear or vanish
• Continuous (subtle) - eigenvalues cross unit circle
• Discontinuous (catastrophic) - eigenvalues appear or vanish
• Explosive - like catastrophic but no hysteresis

(occur when attractor touches the basin boundary)
• There are dozens of bifurcations, many not discovered
• Terminology is not precise or universal (still evolving)
• Transcritical Bifurcation
• A simple form where a stable fixed point becomes unstable
• Or an unstable point becomes stable
• Example:  Fixed points of logistic map
• X* = 0, 1 - 1/A
• At A = 1, stability of points switch
• Exchange of stability between two fixed points
• Pitchfork Bifurcation
• This is a local bifurcation


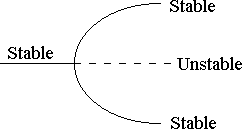
• Stable branch becomes unstable
• Two new stable branches are born
• Happens when eigenvalue of fixed point reaches +1
• This usually occurs when there is a symmetry in the problem
• Flip Bifurcation
• As above but solution oscillates between the branches
• This is the common period-doubling route to chaos
• As occurs in the logistic map at 3 < A < 3.5699
• Happens when eigenvalue of fixed point reaches -1
• Can double and then halve without reaching chaos
• Can occur only in maps (not flows)
• Tangent (or Saddle-Node or Blue Sky) Bifurcation
• This was previously discussed under intermittency
• Provides a new route to chaos
• This is also a local bifurcation
• It is sometimes called an interior crisis
• Basic mechanism for creating and destroying fixed points
• Catastrophe (1-D example)
• Cubic map:  X_n+1 = AX_n(1 - X_n²)


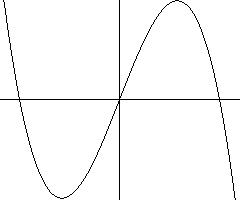
• Anti-symmetric about X_n = 0  (allows negative solutions)


• Catastrophe occurs at A = 27^1/2/2 = 2.59807... where attractors collide
• This system is exhibits hysteresis (decrease in A can leave X < 0)
• Also occurs in two back-to-back logistic maps
• Can also have infinitely many attractors
• Process equation: X_n+1 = X_n + A sin(X_n)
• Fixed points: X* = n pi  for n = 0, + 1, +2, ...
• Attractors collide at A = 4.669201...
• Orbits diffuse in X for A > 4.669201...
• Hopf Bifurcation
• A stable focus becomes unstable and a limit cycle is born
• Example:  Van der Pol equation at b = 0


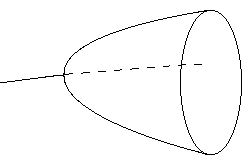
• This bifurcation is local and continuous
• It occurs when complex eigenvalues touch the unit circle
• Niemark (or Secondary Hopf) Bifurcation
• A stable limit cycle becomes unstable and a 2-torus is born


• The Poincaré section exhibits a Hopf bifurcation
• Main sequence (quasi-periodic route to chaos)
• fixed point --> limit cycle --> 2-torus --> chaos
• N-torus with N > 2 not usually seen (Piexito's Theorem)

(3-torus and higher are structurally unstable)
• This contradicts the Landau theory of turbulence

(turbulence is a sum of very many periodic modes)
• Also called the Newhouse-Ruelle-Takens route
• Probably the most common route to chaos at high-D