J. C. Sprott
Introduction
What follows is the derivation of a set of differential
equations describing the dynamics of walking and running. The model is
extremely simple. It assumes the legs are stiff and oscillate at their
natural resonant frequency. Newton’s second law is solved assuming the
mass (m) of the body is concentrated at the top of the legs (length
L)
and moves forward with a constant horizontal velocity (vx).
The transition from walking to running occurs when both feet lose contact
with the ground.
The Model
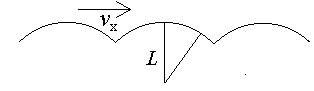 If
the legs are stiff during walking, the body moves forward through a sequence
of circular arcs, like a wheel rotating on its spokes without benefit of
rim. Each foot is in contact with the ground 50% of the time and leaves
the ground at the instant the other touches. As a result, the mass of the
body, assumed concentrated at the top of the legs, moves forward along
a trajectory as shown:
If
the legs are stiff during walking, the body moves forward through a sequence
of circular arcs, like a wheel rotating on its spokes without benefit of
rim. Each foot is in contact with the ground 50% of the time and leaves
the ground at the instant the other touches. As a result, the mass of the
body, assumed concentrated at the top of the legs, moves forward along
a trajectory as shown:
The mass m moves vertically in response to the superposition of two forces, gravity mg (g = 9.8 m/s2) in the downward direction, and an upward normal force N exerted by the ground on the foot. Thus by Newton’s second law, the vertical component of its velocity vy obeys the equation:
mdvy/dt = N – mg
As long as the foot maintains contact with the ground, the mass moves along a circular trajectory with a downward acceleration of approximately vx2/L, from which the required normal force can be calculated as N = mg – mvx2/L.
Note that the normal force is constant and less than mg throughout the circular portion of the trajectory and there is a value of vx at which N reaches zero. For larger values of vx, the foot leaves the ground and the mass moves along a parabolic trajectory rather than a circular trajectory with gravity as the only force. This condition corresponds to the transition from walking to running in this model. The speed at which the transition occurs is vx = (gL)1/2, or about 3 m/s (~ 7 MPH) for a person of average size.
Although the normal force is constant and less that mg throughout the downward curving portion of the trajectory, there must by a large impulsive upward force greater than mg at the cusps where the trajectory abruptly changes from downward to upward. This impulse must equal the integral of the downward force over the remaining interval so that there is no net acceleration of the mass averaged over a cycle. Hence I = (mg – N)T/2, where T is the natural period of oscillation of a leg. This impulse changes the vertical component of the momentum by mDvy = I, from which the initial value of vy can be calculated, vy(0) = Dvy/2 = I/2m = (g – N/m)T/4, where N = max[0, mg – mvx2/L].
From Newton’s second law the dynamical equations can thus be derived:
dy/dt = vy
dvy/dt = max(0, g – vx2/L) - g
The transition from walking to running is smooth at the value calculated
above, and there is no qualitative change in the trajectory of the mass.
Power Requirement
The average power required to move forward at velocity vx can be estimated by assuming that one has to supply the energy mgh to raise the center of mass through a height h each half cycle, and that none of this energy is recovered. The average power is thus P = 2mgh / T. The height h can be calculated from h = vy(0)T/8, from which the power can be calculated:
P = mgvy(0)/4 = (g – max[0, g – vx2/L])mgT/4
For walking at low speed, the power is PW = vx2mgT/4L, whereas for running the power is PR = mg2T/4. At the transition speed, the power required for m = 50 kg and T = 0.5 s is about 600 W. Walking is generally performed with a period close to the natural resonance of the leg, T = 2p(2L/3g)1/2, whereas for running, one can increase the period to achieve higher speed, with a corresponding proportional increase in the required power. At this optimal period, the initial vertical velocity when walking is vy(0) = pvx/61/2 = 1.283vx. It is reasonable to assume that this ratio of vy(0)/vx also persists for running since it is close to the optimum ratio of 1.0 at which the maximum distance is traveled per step. Under this assumption, the power expended in running is PR = pmgvx/61/2, whereas for walking it is PW = pmgvx2/(gL)1/2/6. If the walk-run transition occurs at vx = (gL)1/2, as postulated above, this corresponds to the point at which the two power curves cross. Thus the general expression for the power consumed in walking and running is
P = 1.283 mgvx min[1, vx/(gL)1/2]
Finally the general expression for the initial vertical velocity subject to the above assumptions is
vy(0) = 1.283 vx max[1, (1 – max[0, 1 – vx2/gL])]
This initial condition along with the dynamical equations above provide a complete description of the motion for all values of vx within the assumptions of this rather idealized model.