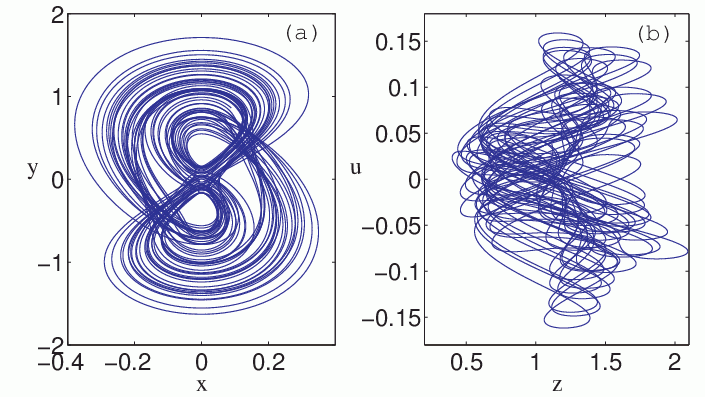
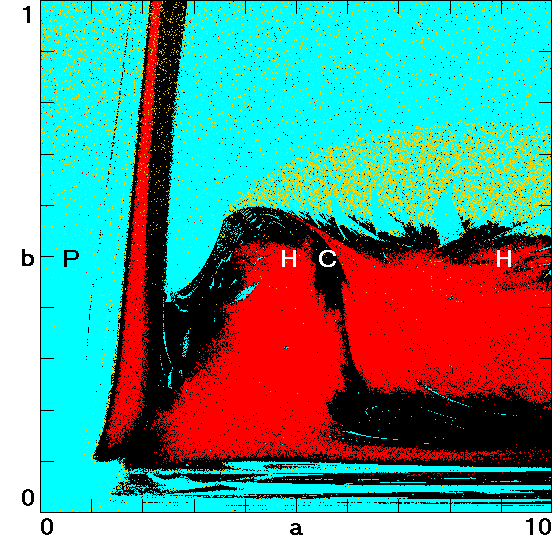
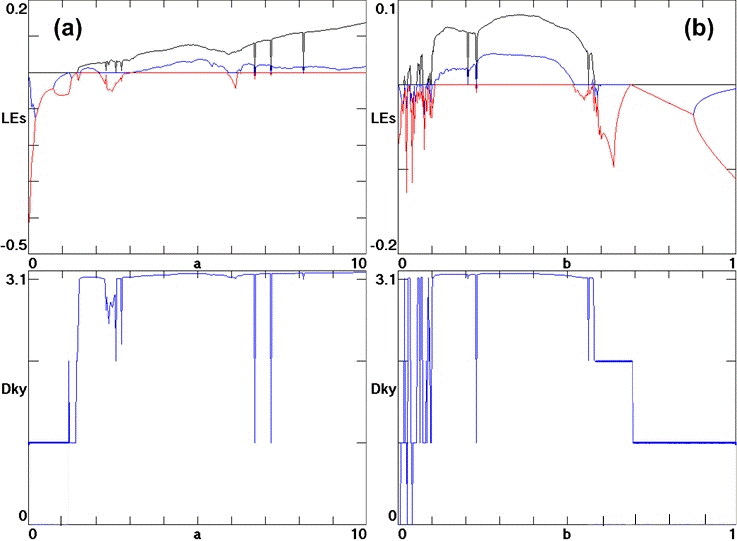
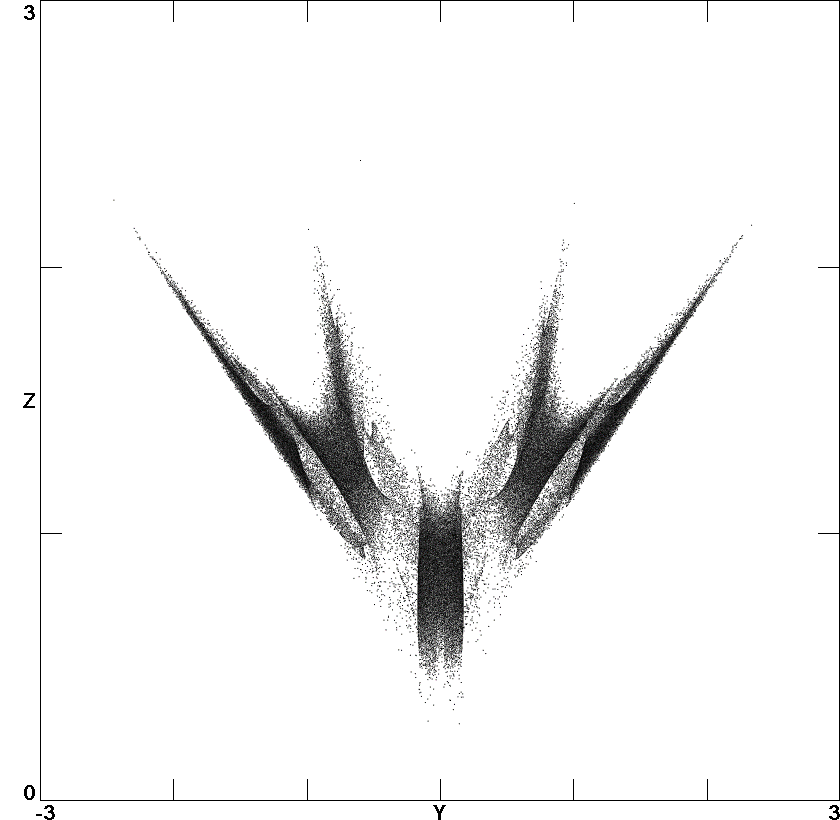Bistability in a Hyperchaotic System with a Line Equilibrium

Chunbiao Lia, J.C.Sprottb, Wesley Thioc
aSchool of Information Science and Engineering, Southeast University 210096, Nanjing, China
bDepartment of Physics, University of Wisconsin-Madison 53706, Madison, WI, USA
cDepartment of Electrical and Computer Engineering, The Ohio State University 43210, Columbus, OH, USA
Received October 26, 2013

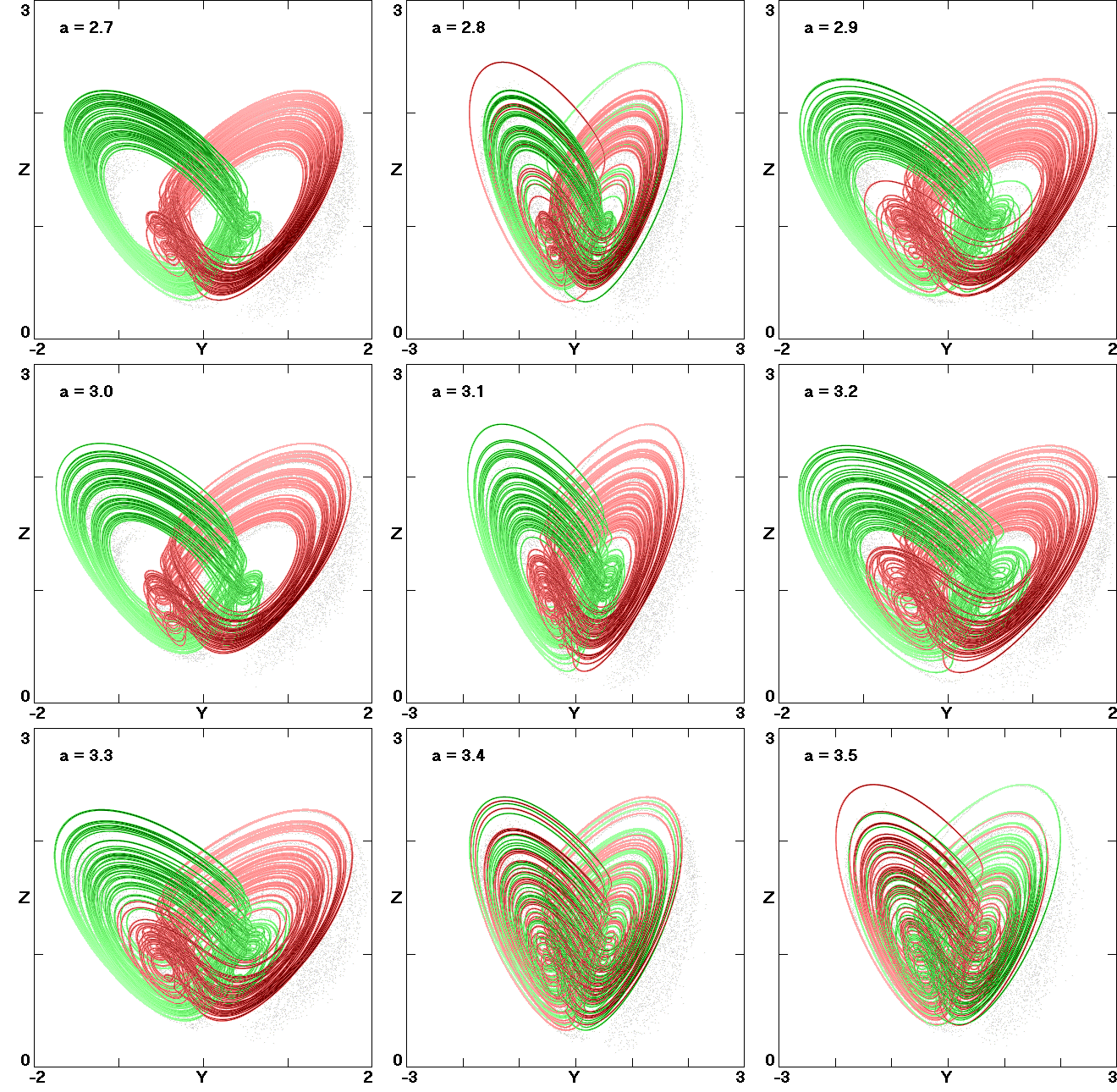
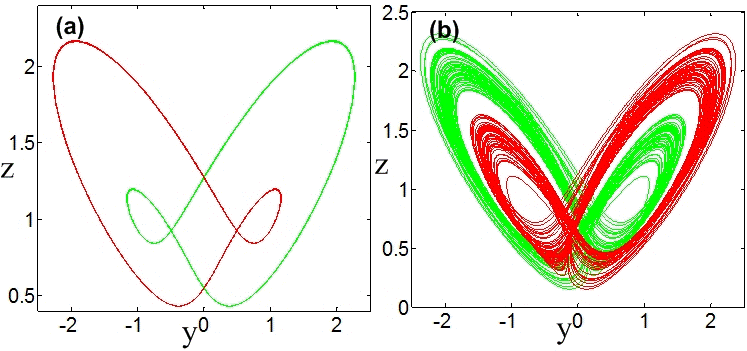
A hyperchaotic system with an infinite line of equilibrium points is described. A criterion is proposed for quantifying the hyperchaos, and the position in the three-dimensional parameter space where the hyperchaos is largest is determined. In the vicinity of this point, different dynamics are observed including periodicity, quasi-periodicity, chaos, and hyperchaos. Under some conditions, the system has a unique bistable behavior, characterized by a symmetric pair of coexisting limit cycles that undergo period doubling, forming a symmetric pair of strange attractors that merge into a single symmetric chaotic attractor that then becomes hyperchaotic. 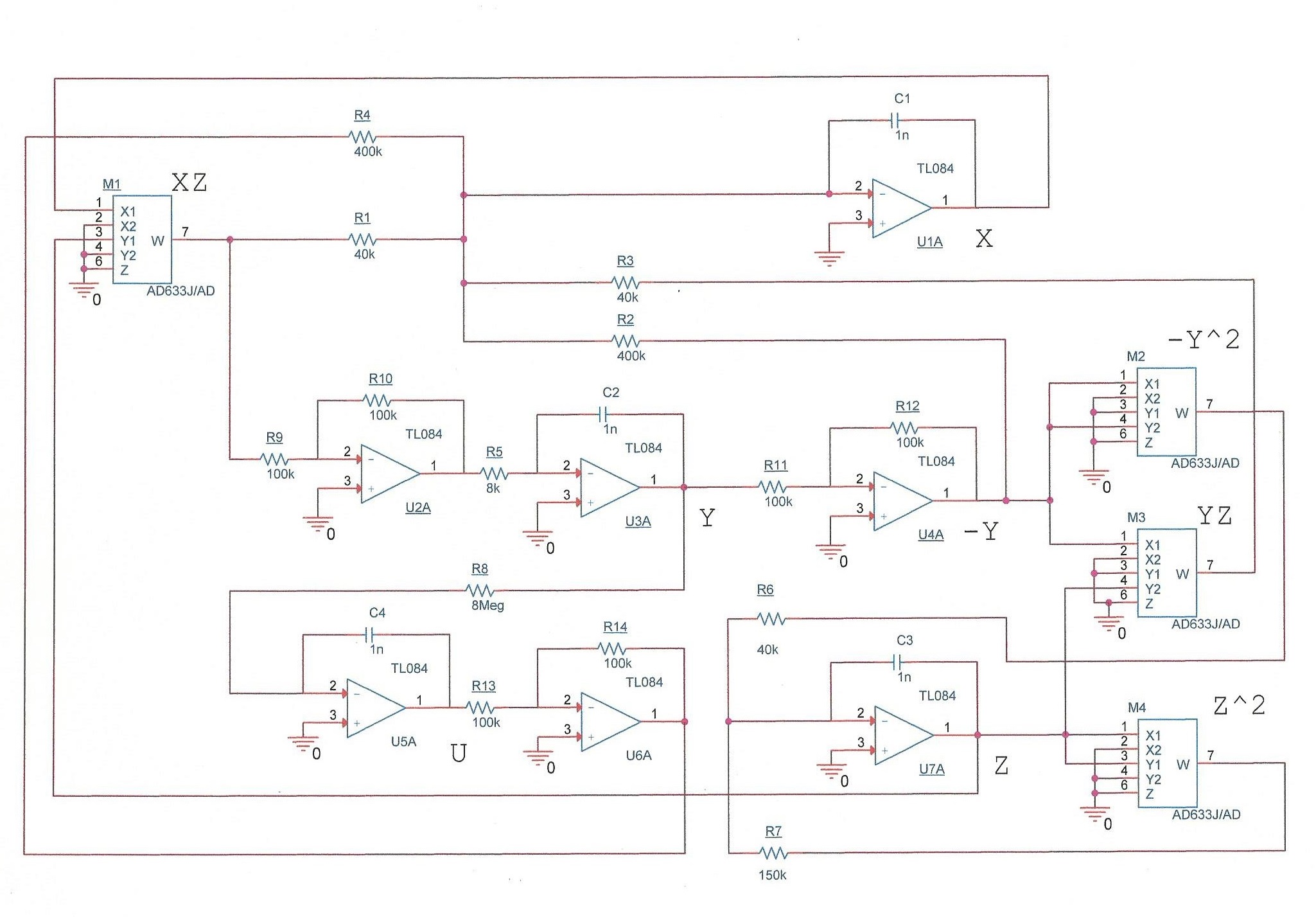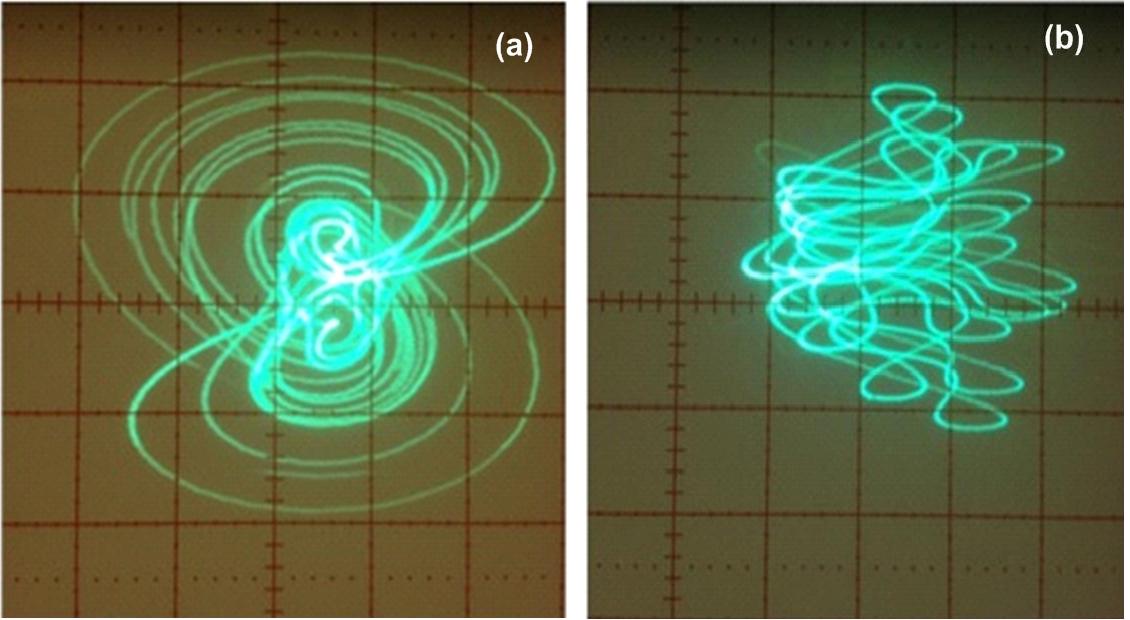The system was implemented as an electronic circuit whose behavior confirms the numerical predictions.

Ref: C. Li, J. C. Sprott, and W. Thio, Journal of Experimental and Theoretical Physics 118, 494-500 (2014)

The complete paper is available in PDF format.

Return to Sprott's Books and Publications.
Figure 1

Fig. 1
Figure 2
Fig. 2
Figure 3
Fig. 3
Figure 4
Fig. 4
Figure 5
Fig. 5
Figure 6
Fig. 6
Figure 7
Fig. 7
Figure 8
Fig. 8