Generalization of the Simplest Autonomous Chaotic System

Buncha Munmuangsaena, Banlue Srisuchinwonga, J.C. Sprottb
aSirindhorn International Institute of Technology (SIIT), Thammasat University, Pathum-Thani 12000, Thailand
bDepartment of Physics, University of Wisconsin, Madison, WI 53706, USA

Received 19 October 2010, Received in revised form 7 February 2011, Accepted 12 February 2011, Available online 16 February 2011

ABSTRACT

An extensive numerical search of jerk systems of the form x''' + x'' + x = f (x') revealed many cases with chaotic solutions in addition to the one with f (x') = x'2 that has long been known. Particularly simple is the piecewise-linear case with f (x') = α(1− x') for x' > 1 and zero otherwise, which produces chaos even in the limit of α→∞. The dynamics in this limit can be calculated exactly, leading to a two-dimensional map. Such a nonlinearity suggests an elegant electronic circuit implementation using a single diode.

Ref: B. Munmuangsaen, B. Srisuchinwong, and J.C. Sprott, Phys. Lett. A 375, 1445-1450 (2011)

The complete paper is available in PDF format.

Return to Sprott's Books and Publications.


Fig. 1. Attractors of Eq. (3) for each of the nonlinear functions in Table 1.
Figure 1

Fig. 2. The largest Lyapunov exponent and bifurcation diagram of Eq. (3) for f (x') = −A exp(x') with 0 < A < 0.5.
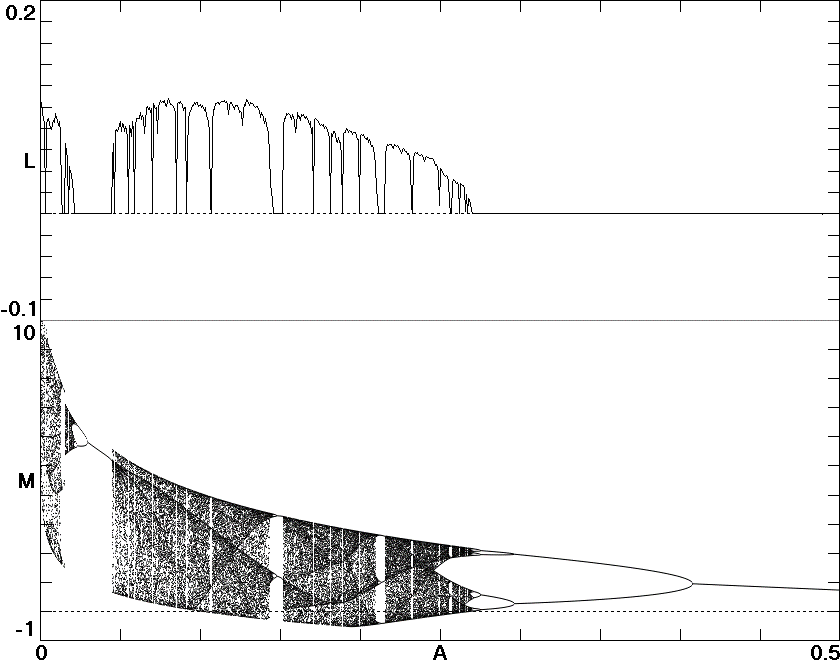
Figure 1

Fig. 3. Homoclinic orbit in Eq. (3) for f (x') = −A exp(x') with A = 0.1306.
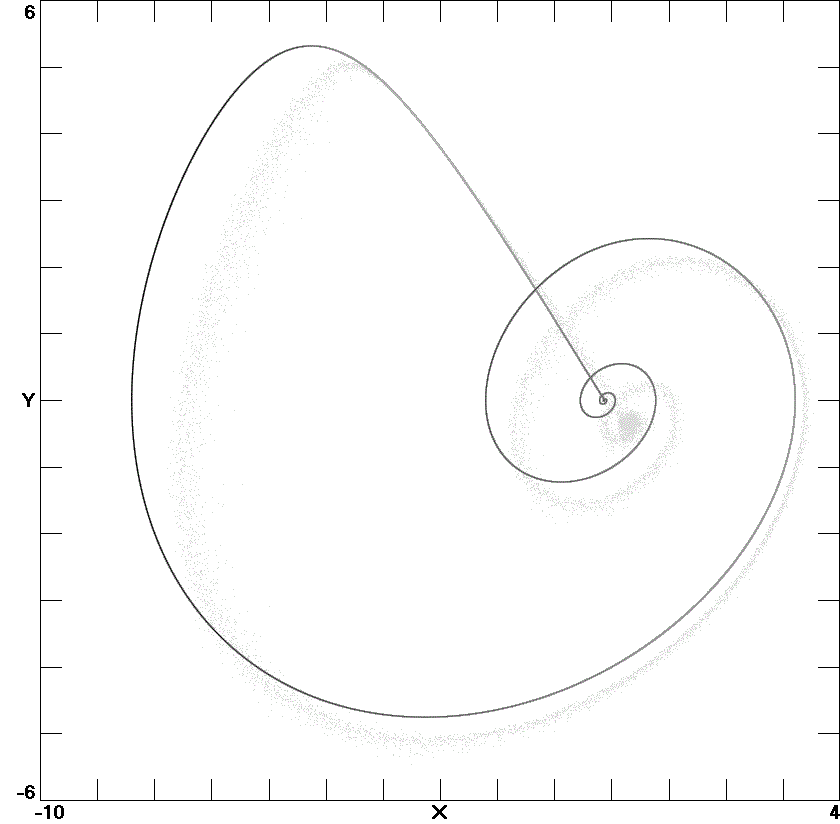
Figure 3

Fig. 4. Attractor for the piecewise-linear system.
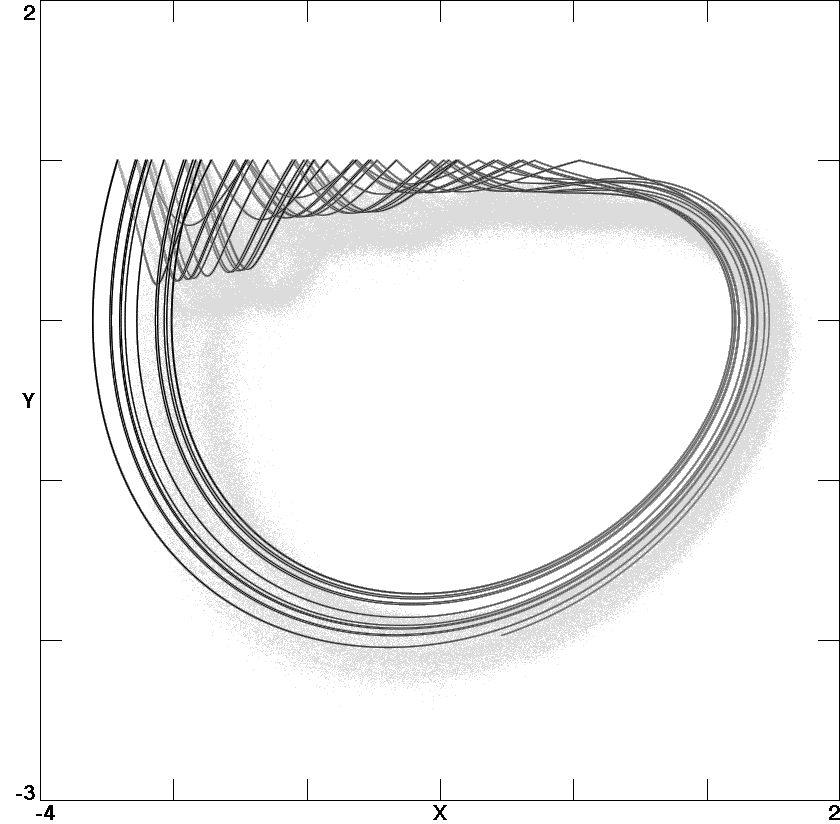
Figure 4

Fig. 5. Poincaré section at x' = 0 for the piecewise-linear system.
Figure 5

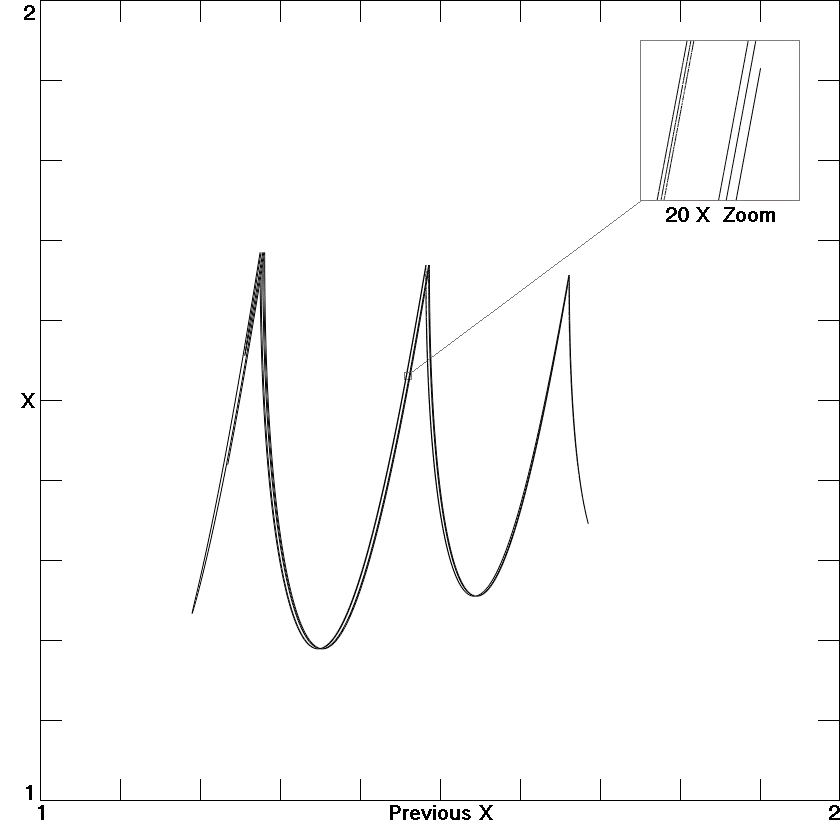
Fig. 6. Return map for the maximum value of x for the piecewise-linear system.
Figure 6