Simple Driven Chaotic Oscillators with Complex Variables
Delmar Marshall
Department of Physics, Amrita Vishwa Vidyepeetham, Clappana 690-525,
India
J. C. Sprott
Departments of Physics, University
of Wisconsin, 1150 University Avenue, Madison, WI 53706, USA
(Received 12 November 2008; accepted 21 January 2009; published online
5 March 2009)
ABSTRACT
Despite a search, no chaotic driven complex-variable oscillators of the
form z˙+ f(z)
= eiwt or z˙+ f(z¯�)
= eiwt are found, where f is a
polynomial with real coefficients. It is shown that, for analytic
functions f(z), driven complex-variable
oscillators of the form z˙+ f(z)
= eiwt cannot have chaotic
solutions. Seven simple driven chaotic
oscillators of the form z˙+ f(z,
z¯�) = eiwt with polynomial f(z,
z¯)� are given. Their
chaotic attractors are displayed, and
Lyapunov spectra are calculated. Attractors for two of the cases have
symmetry across the x = −y line. The systems’ behavior with
�w as a
control parameter in the range of w
= 0.1–2.0 is examined, revealing
cases of period doubling, intermittency, chaotic transients, and period
adding as routes to chaos. Numerous cases of coexisting attractors are
also observed.
Ref: D. Marshall and J. C. Sprott,
Chaos 19, 013124-1 - 013124-7
(2009)
The complete paper is available
in PDF format.
Return to Sprott's Books and Publications.
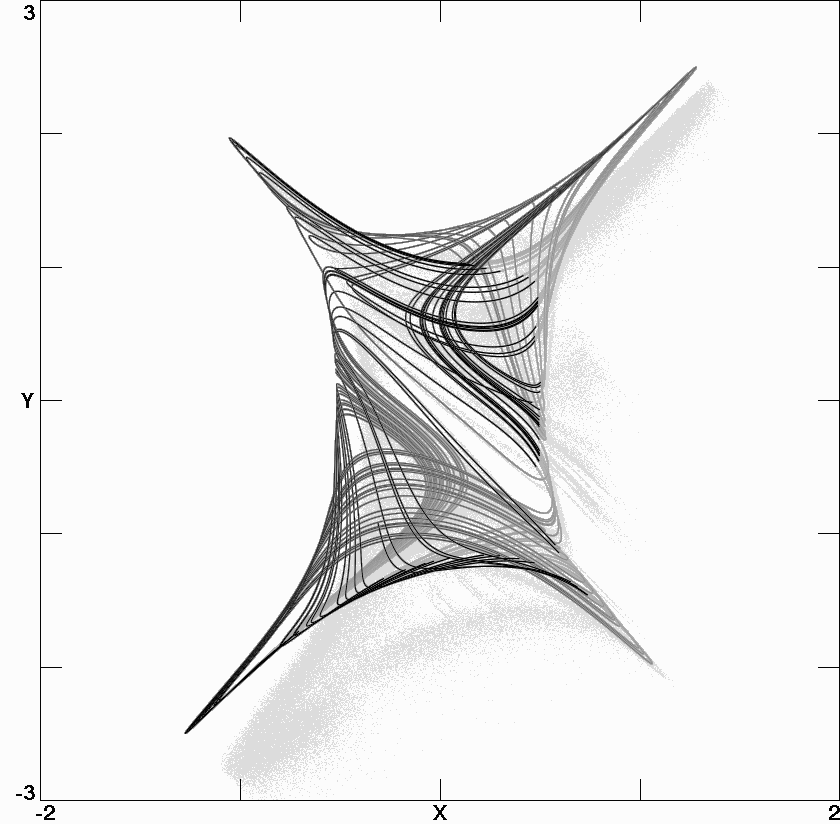
Fig. 1.
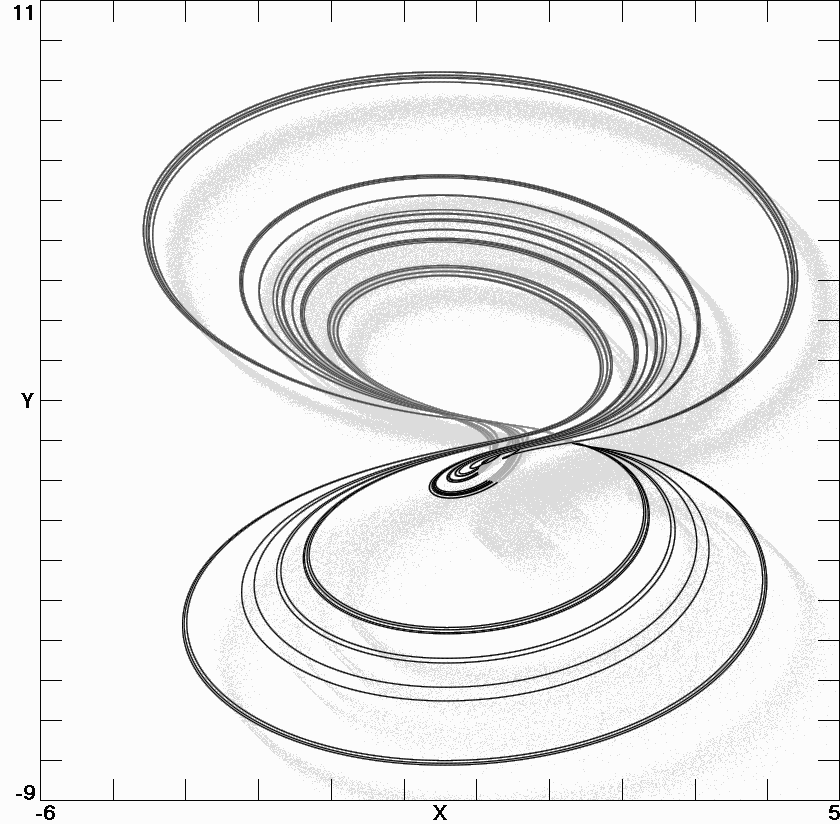
Fig. 2.
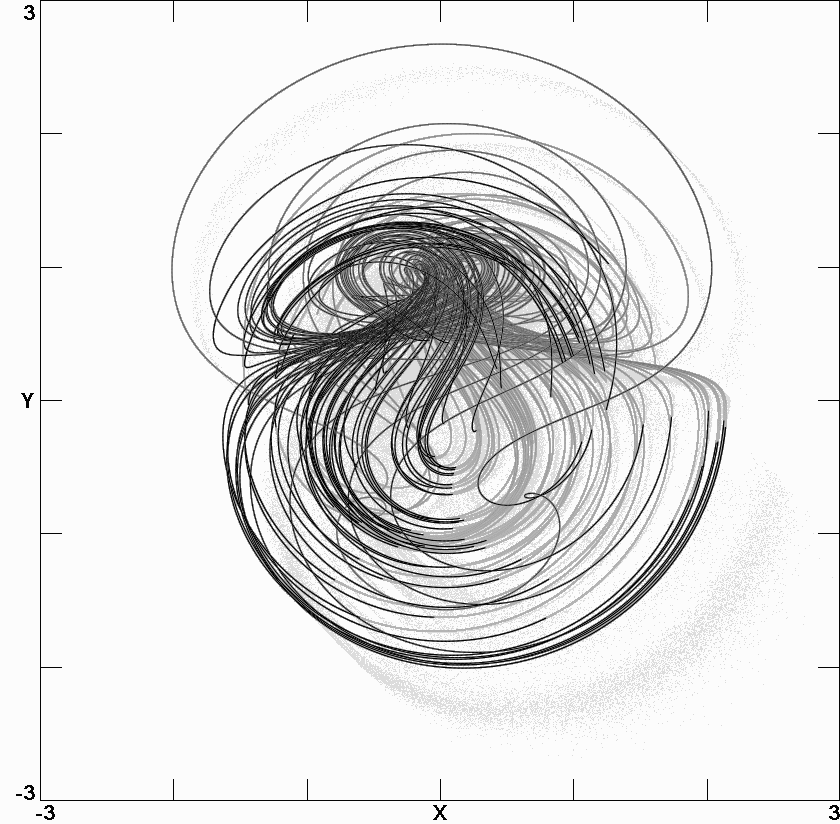
Fig. 3.
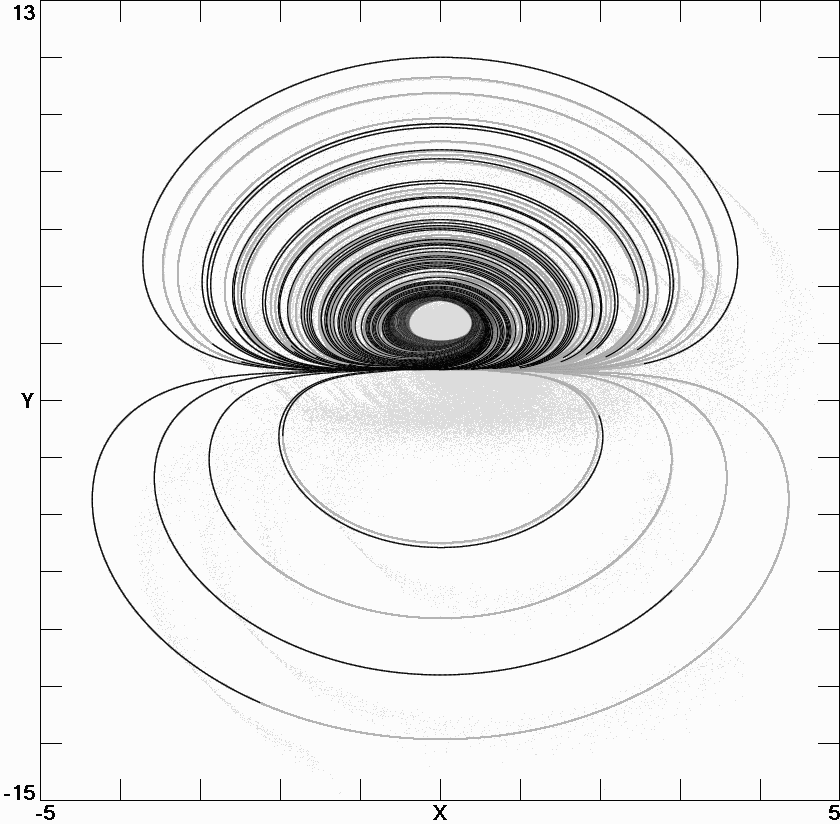
Fig. 4.

Fig. 5.
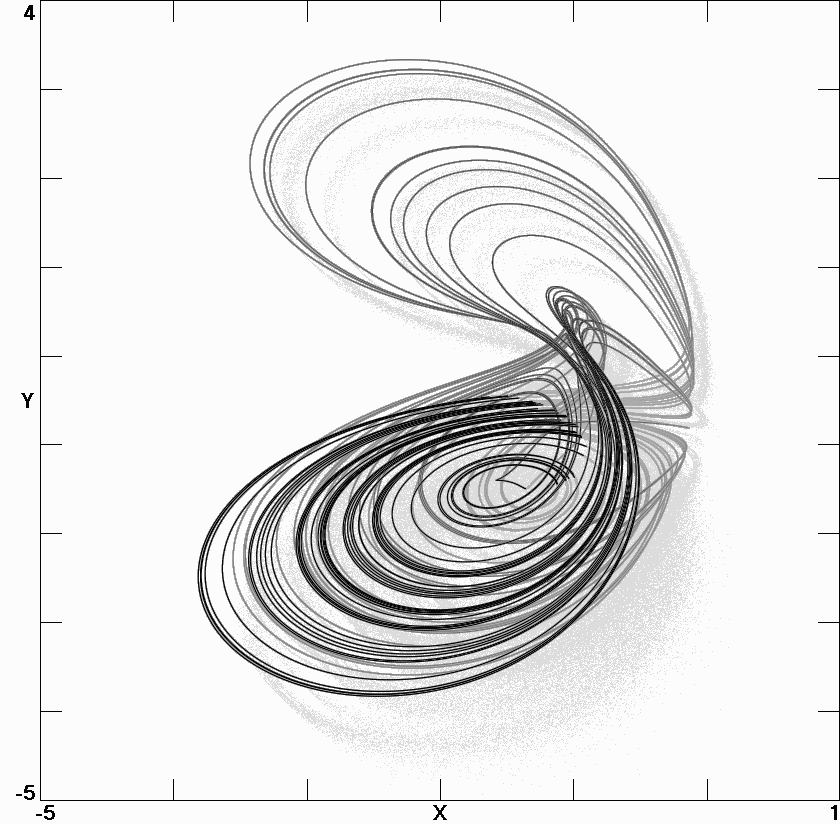
Fig. 6.
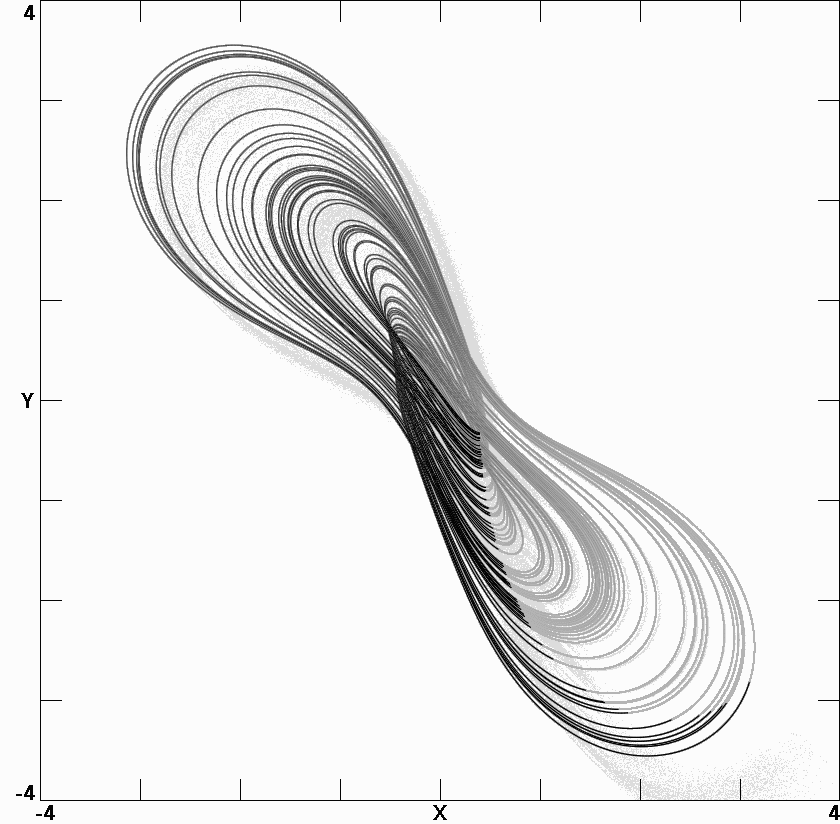
Fig. 7.
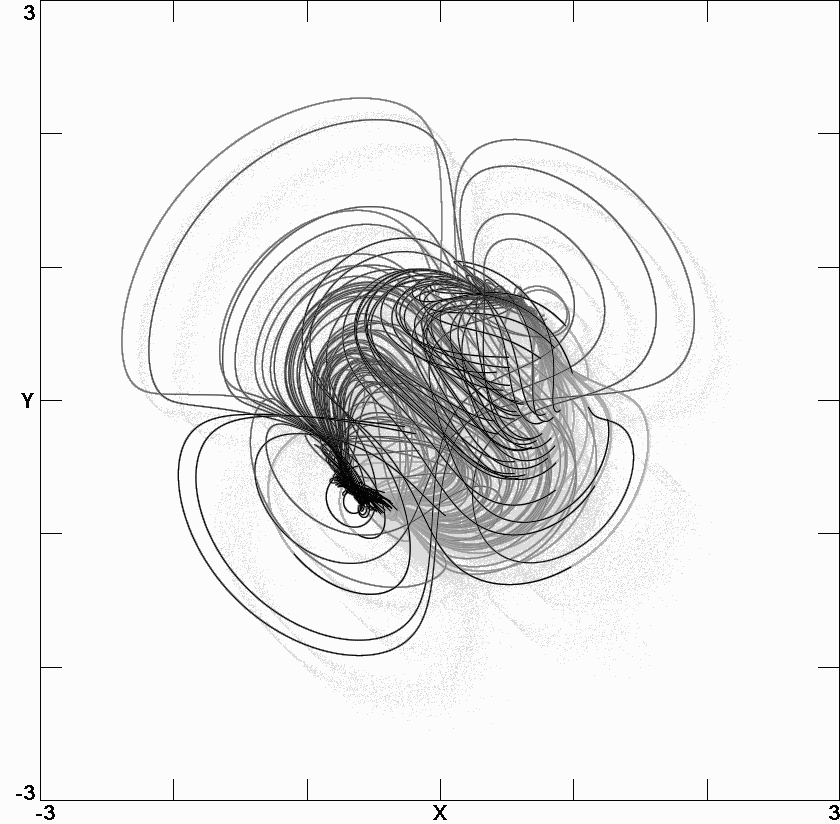
Fig. 8.