Maximally Complex Simple Attractors

J. C. Sprott
Departments of Physics, University of Wisconsin, 1150 University Avenue, Madison, Wisconsin 53706, USA

(Received 12 July 2007; accepted 17 August 2007; published online 28 September 2007)

ABSTRACT

A relatively small number of mathematically simple maps and flows are routinely used as examples of low-dimensional chaos. These systems typically have a number of parameters that are chosen for historical or other reasons. This paper addresses the question of whether a different choice of these parameters can produce strange attractors that are significantly more chaotic (larger Lyapunov exponent) or more complex (higher dimension) than those typically used in such studies. It reports numerical results in which the parameters are adjusted to give either the largest Lyapunov exponent or the largest Kaplan-Yorke dimension. The characteristics of the resulting attractors are displayed and discussed.

Ref: J. C. Sprott, Chaos 17, 031124-1 - 031124-6 (2007)

The complete paper is available in PDF format.

Return to Sprott's Books and Publications.


Fig. 1. Lyapunov exponent for the general symmetric map showing peaks at alpha = 1 (tent map) and alpha = 2 (logistic map) where its value is ln(2).
Figure 1


Fig. 2. Attractor for the maximally complex Henon map with alpha = 1 and b = 0.542 72 along with its basin of attraction.
Figure 2


Fig. 3. Attractor for the maximally complex Lozi map with a = 1.7052 and b = 0.5896 along with its basin of attraction.
Figure 3


Fig. 4. Attractor for the maximally chaotic normalized Lorenz system with alpha = 0.300, gamma = 0.028, and beta = 0.250.
Figure 4


Fig 5. Attractor for the maximally complex Lorenz system with R = 3.4693.
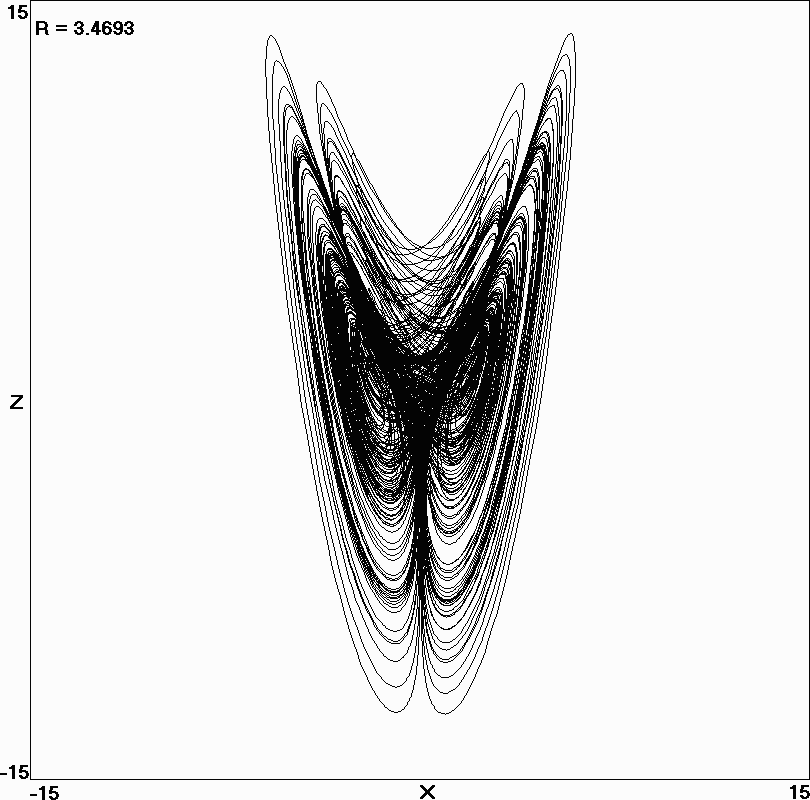
Figure 5


Fig. 6. Poincaré section at y = 0 for the maximally complex Lorenz system with R = 3.4693.
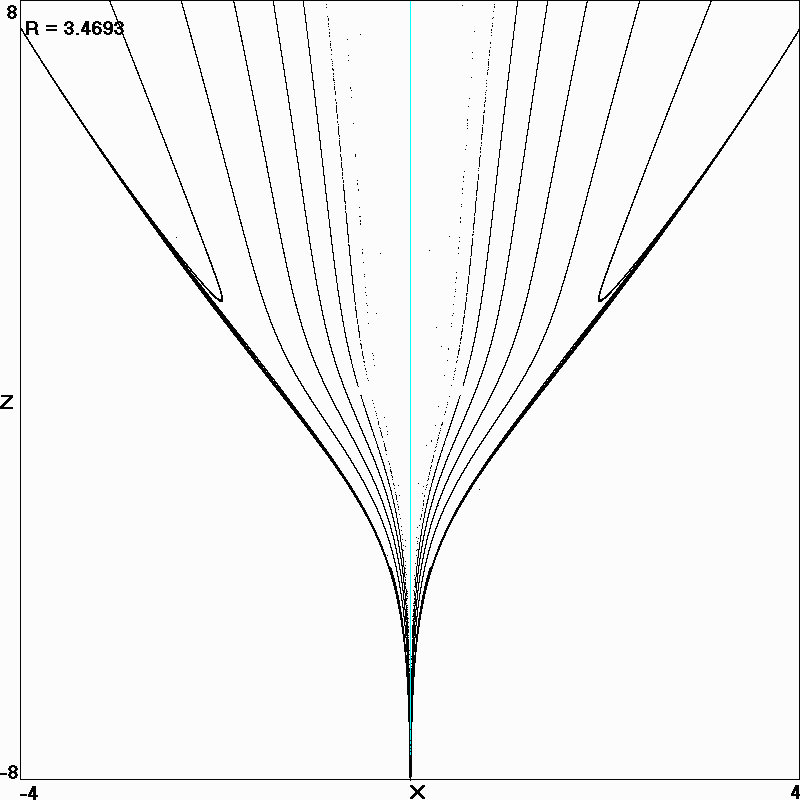
Figure 6


Fig. 7. Variation of the Kaplan-Yorke dimension with the parameter R for the diffusionless Lorenz system in Eq. (8).
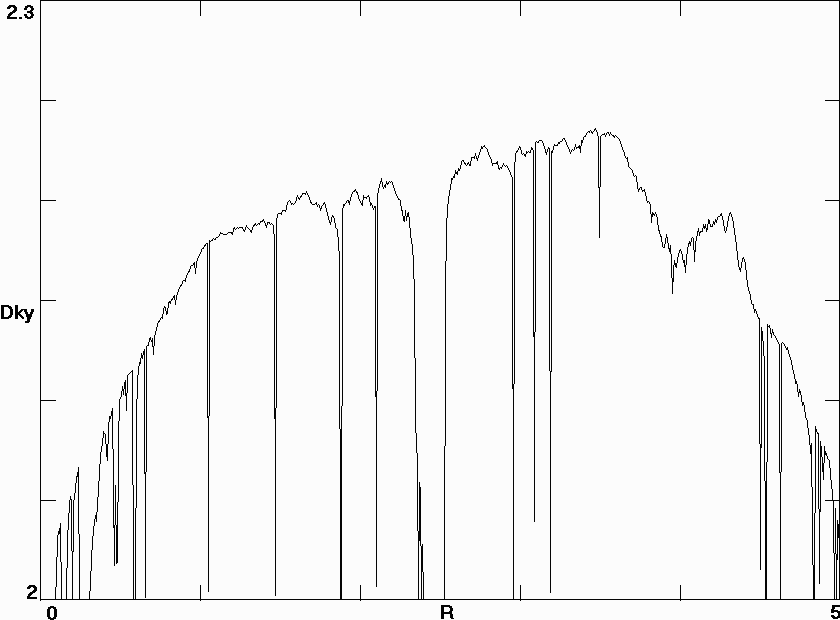
Figure 7


Fig. 8. Attractor for the maximally chaotic Rössler system with a = 0.395, b = 0.487, and c = 8.164.
Figure 8


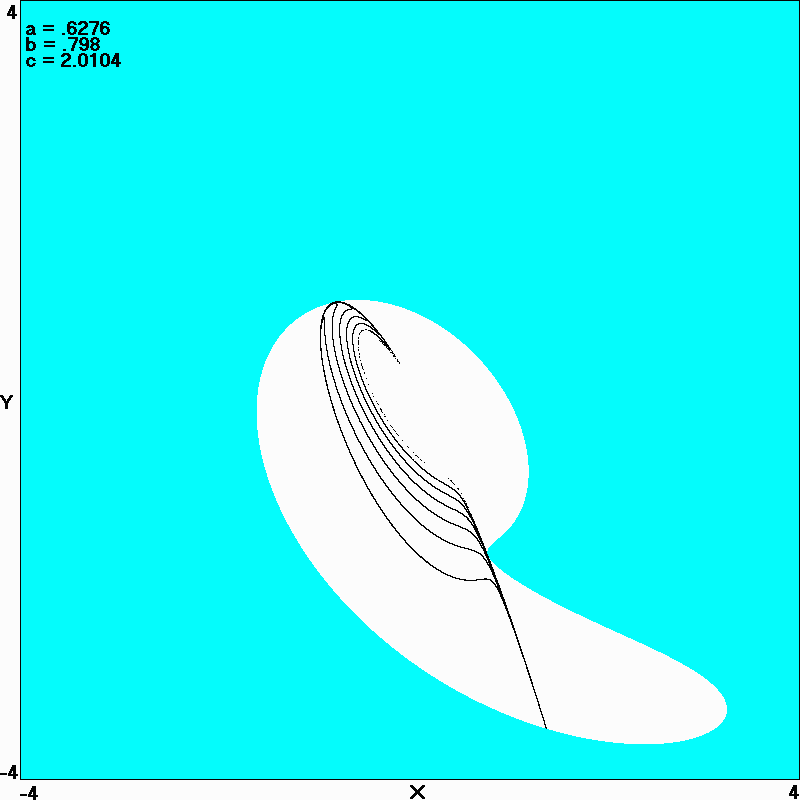
Fig. 9. Attractor for the maximally complex Rössler system with a = 0.6276, b = 0.7980, and c = 2.0104.
Figure 9


Fig. 10. Poincaré section at z = z-* for the maximally complex Rössler system with a = 0.6276, b = 0.7980, and c = 2.0104.
Figure 10