Fig. 1. Eigenvalues of the coexisting equilibrium with N = 100 and s = 1.
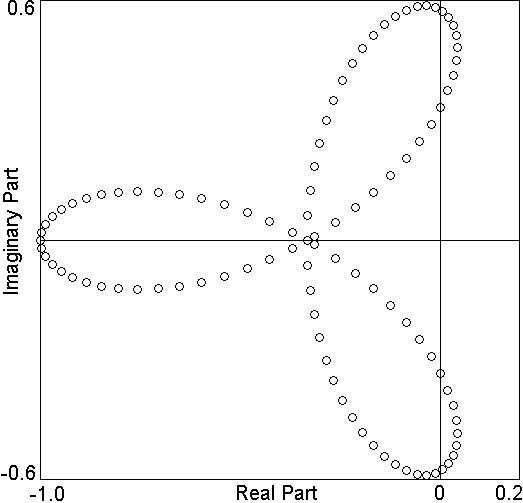
Fig. 2. A one-dimensional ring of species interacting according to
Eq. (2).
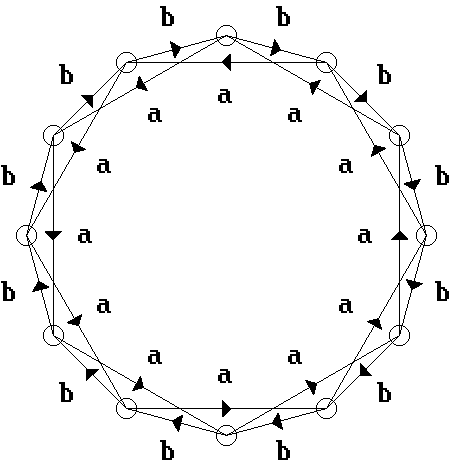
Fig. 3. Largest Lyapunov exponent and Kaplan-Yorke dimension for Eq.
(2) with s = 1.
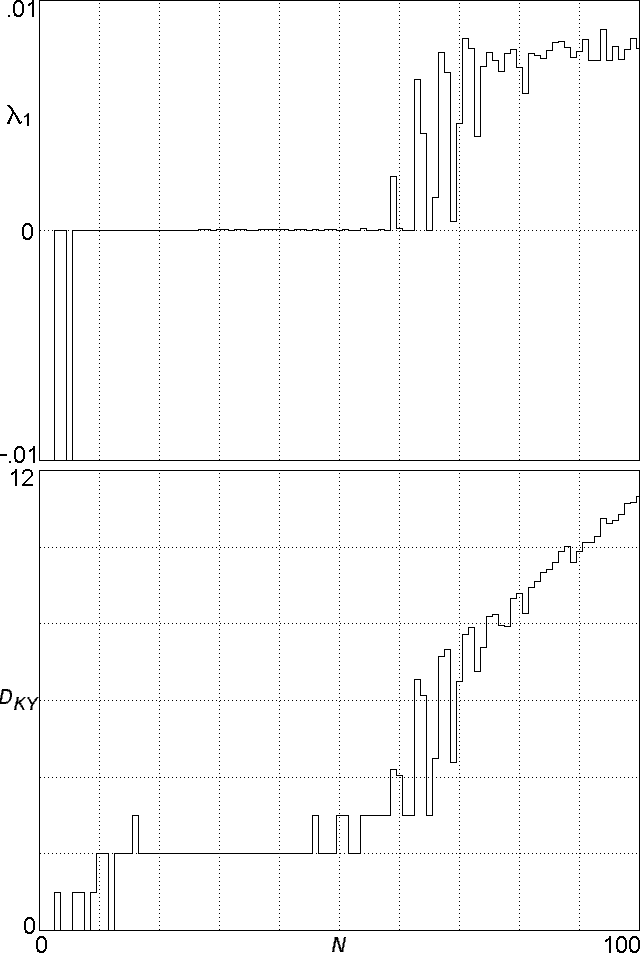
Fig. 4. Largest Lyapunov exponent for
Eq. (2) with N = 100 showing
the quasiperiodic route to chaos that is typical of high-dimensional
systems.
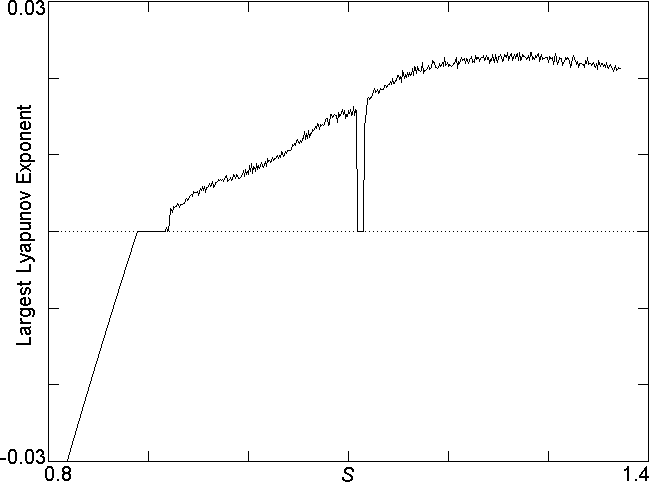

Fig. 5. Spatiotemporal plot of |xi+1 - xi| from Eq. (2) with N = 480 and s = 1.

Fig. 6. Spatiotemporal cross-correlation function with N = 100 and s = 1 showing propagation and dispersion.
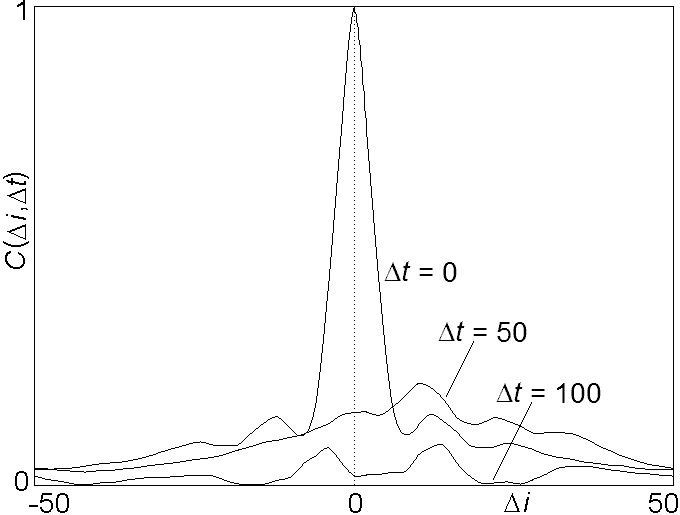
Fig. 7. Total biomass, biodiversity, and a typical x(t) versus time for Eq. (2) with N = 100 and s = 1.
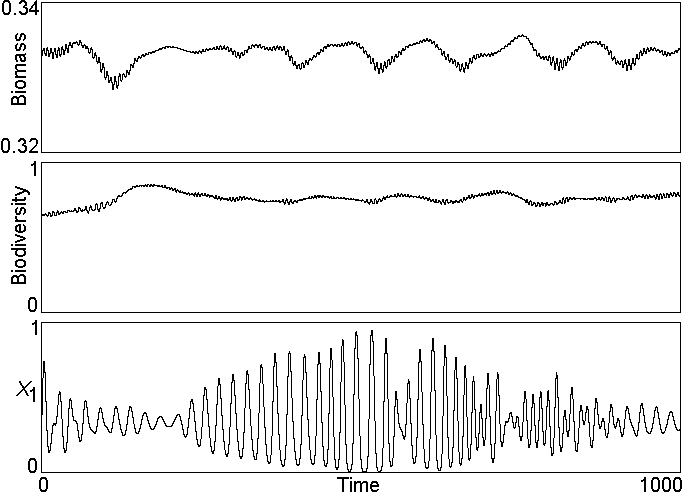

Fig. 6. Spatiotemporal cross-correlation function with N = 100 and s = 1 showing propagation and dispersion.

Fig. 7. Total biomass, biodiversity, and a typical x(t) versus time for Eq. (2) with N = 100 and s = 1.
