Dynamical Models of Happiness

J. C. Sprott
Department of Physics, University of Wisconsin - Madison

ABSTRACT

A sequence of models for the time evolution of one's happiness in response to external events is described. These models with added nonlinearities can produce stable oscillations and chaos even without external events. Potential implications for psychotherapy and a personal approach to life are discussed.

Ref: J. C. Sprott, Nonlinear Dynamics, Psychology, and Life Sciences 9, 23-36 (2005).

The complete paper is available in PDF format.

See the companion paper on Dynamical Models of Love

A less technical, more personal version of this is in Chapter 18 of my Memoirs.

Return to Sprott's Books and Publications.

Fig. 1. Possible responses of the happiness model in Eq. 1 to an isolated event.

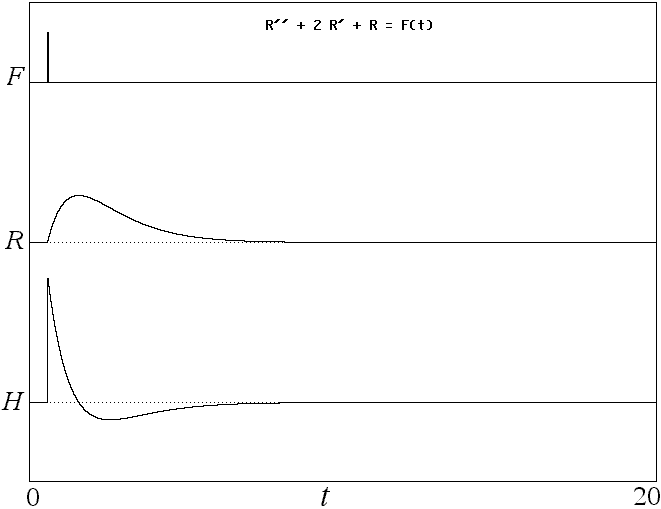
Fig. 2. Response of happiness (H) to a single event like winning the lottery from Eq. 1 with critical damping.

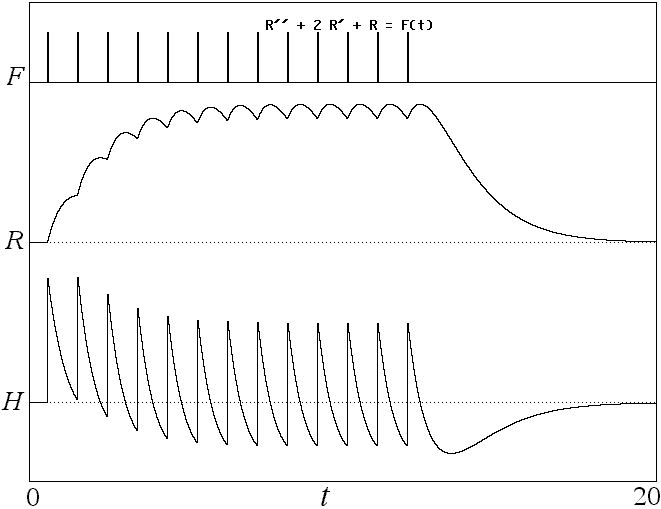
Fig. 3. Response of happiness (H) to a periodic stimulus such as drug addiction from Eq. 2.

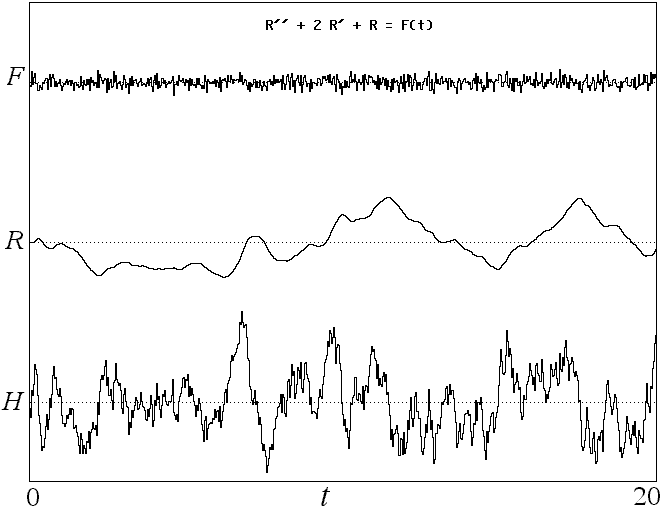
Fig. 4. Response of happiness (H) to Gaussian white noise typical of real life from Eq. 2.

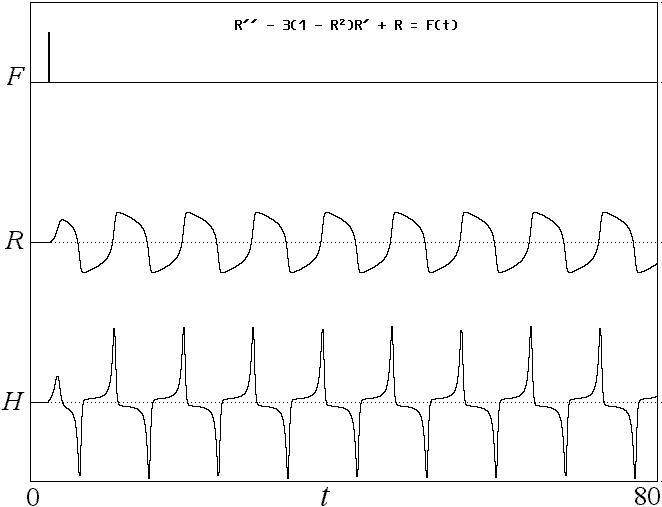
Fig. 5. Limit cycle behavior modeling a bipolar disorder from Eq. 3.

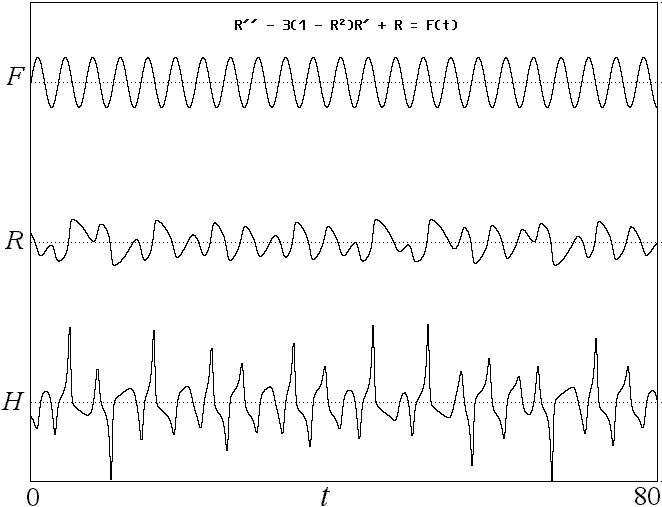
Fig. 6. Chaotic behavior of happiness (H) with a periodic forcing from Eq. 3.

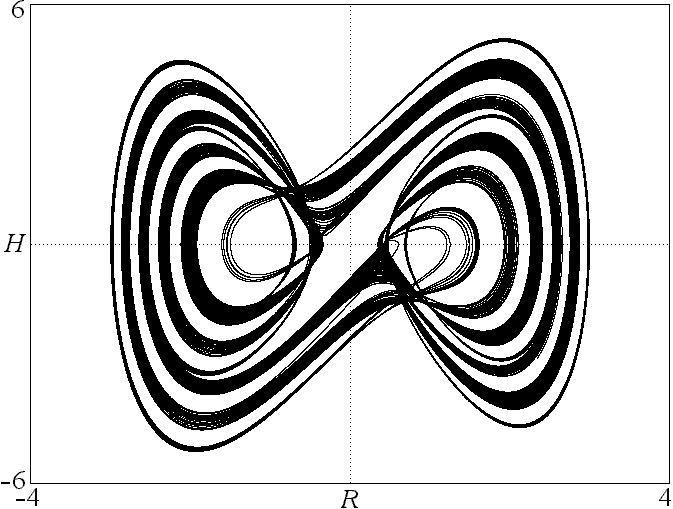
Fig. 7. Strange attractor from the happiness model with anticipation in Eq. 4.