On the Probability of Chaos in Large Dynamical Systems: A Monte Carlo Study

W. Davis Dechert
Department of Economics, University of Houston, Houston, USA

Julien C. Sprott, David J. Albers
Department of Physics, University of Wisconsin, Madison, USA

Received 29 August 1995; accepted 1 July 1997

ABSTRACT

In this paper we report the result of a Monte Carlo study on the probability of chaos in large dynamical systems. We use neural networks as the basis functions for the system dynamics and choose parameter values for the networks randomly. Our results show that as the dimension of the system and the complexity of the network increase, the probability of chaotic dynamics increases to 100%. Since neural networks are dense in the set of dynamical systems, our conclusion is that most large systems are chaotic.

Ref: W. D. Dechert, J. C. Sprott, and D. J. Albers, Journal of Economic Dynamics and Control 23, 1197-1206 (1999)

The complete paper is available in PDF format.

Return to Sprott's Books and Publications.

Fig. 1. Contour plot for n = 8 with increasing d and s showing that the probability of chaos approaches unity as d becomes large.

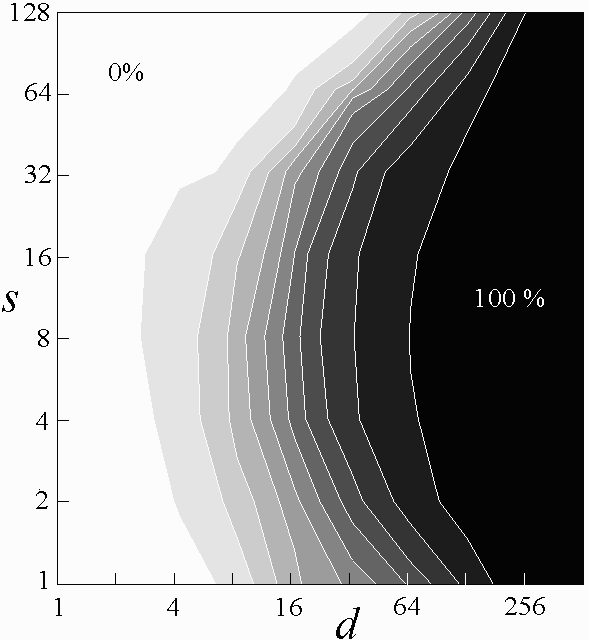
Fig. 2. Contour plot for s = 8 with increasing n and d showing that the probability of chaos approaches unity as d becomes large.

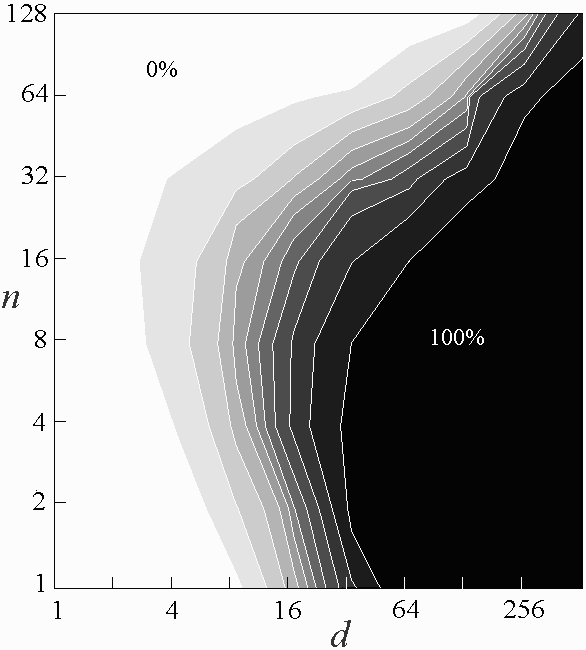
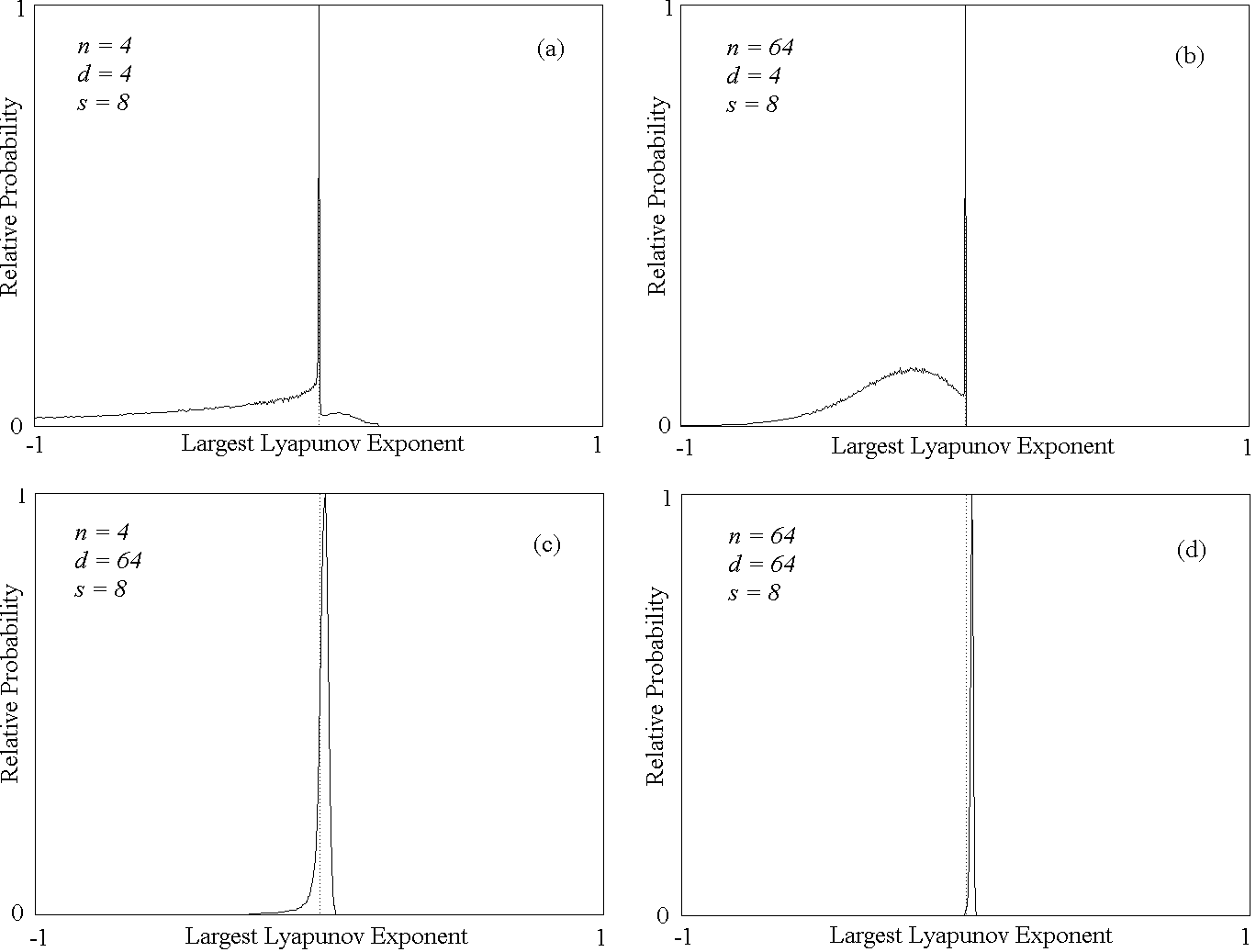
Fig. 3. Distributions of largest Lyapunov exponents for various n and d with s = 8.

The programs and data are available at the World Wide Web site: https://sprott.physics.wisc.edu/neural/.