Lyapunov Exponents

Comments on Homework #3 (Van der Pol Equation)

• Some people only took initial conditions inside the attractor
• For b < 0 the attractor becomes a repellor (time reverses)
• The driven system can give limit cycles and toruses but not chaos (?)
• Can get chaos if you drive the dx/dt equation instead of dy/dt

Review (last week) - Dynamical Systems Theory

• Types of attractors/repellors:
• Equilibrium points (radial, spiral, saddle) 0-D
• Limit cycles (closed loops) 1-D
• 2-Toruses (quasiperiodic surfaces) 2-D
• N-Toruses (hypersurfaces) N-D
• Strange attractors (fractal) Non-integer D

(Attractor dimension < system dimension)
• Stability of equilibrium points:
• Find equilibrium point: f(x) = 0  ==> x*, etc.
• Calculate partial derivatives f_x etc. at equilibrium
• Construct the Jacobian matrix J
• Find the characteristic equation:  det(J - l) = 0
• Solve for the D eigenvalues:  l₁, l₂, ...l_D
• Find the eigenvectors (if needed) from JR = lR
• Stable and unstable manifold (inset & outset)
• Organize the phase space
• Plot position of eigenvalues in complex-plane
• If any have Re(l) > 0, point is unstable
• Index is number of eigenvalues with Re(l) > 0
• Dimension of outset = index
• Volume expansion:  dV/dt / V = l₁ + l₂ + l₃ + ...
• By convention, l₁ > l₂ > l₃ > ...
• An attractor has dV/dt < 0
• Different rules for stability of fixed points for maps
• In 1-D, X = X₀lⁿ is stable if |l| < 1
• In 2-D and higher, stable if all l are inside unit circle
• Bifurcations occur when l touches unit circle
• Examples of chaotic dissipative flows in 3-D:
• Driven pendulum
• dx/dt = v
• dv/dt = -sin x - bv + A sin wt
• A = 0.6,  b = 0.05,  w = 0.7
• Driven nonlinear oscillator (Ueda)
• dx/dt = v
• dv/dt = -x³ - bv + A sin wt
• A = 2.5,  b = 0.05,  w = 0.7
• Driven Duffing oscillator
• dx/dt = v
• dv/dt = x - x³ - bv  + A sin wt
• A = 0.7,  b = 0.05,  w = 0.7
• Driven Van der Pol oscillator
• dx/dt = v
• dv/dt = -x + b(1 - x²)v + A sin wt
• A = 0.61,  b = 1,  w = 1.1  (a torus)
• Can get chaos with drive in dx/dt equation
• Lorenz attractor
• dx/dt = p(y - x)
• dy/dt = -xz + rx - y
• dz/dt = xy - bz
• p = 10,  r = 28,  b = 8/3
• Rössler attractor
• dx/dt = -y - z
• dy/dt = x + ay
• dz/dt = b + z(x - c)
• a = b = 0.2,  c = 5.7
• Simplest dissipative chaotic flow
• dx/dt = y
• dy/dt = z
• dz/dt = -x + y² - Az
• A = 2.107
• Other simple chaotic flows

General Properties of Lyapunov Exponents

• A measure of chaos (how sensitive to initial conditions?)
• Lyapunov exponent is a generalization of an eigenvalue
• Average the phase-space volume expansion along trajectory
• 2-D example:
• Circle of initial conditions evolves into an ellipse


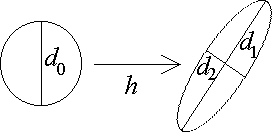
• Area of ellipse:  A = pd₁d₂ / 4
• Where d₁ = d₀e^l1^t is the major axis
• And d₂ = d₀e^l2^t is the minor axis
• Magnitude and direction continually change
• We must average along the trajectory
• As with eigenvalues, dA/dt / A = l₁ + l₂
• Note:  l is always real (sometimes base-2, not base-e)
• For chaos we require l₁ > 0  (at least one positive LE)
• By convention, LEs are ordered from largest to smallest

l₁ > l₂ > l₃ > ...
• In general for any dimension:
• (hyper)sphere evolves into (hyper)ellipsoid
• One Lyapunov exponent per dimension
• Units of Lyapunov exponent:
• Units of l are inverse seconds for flows
• Or inverse iterations for maps
• Alternate units:  bits/second or bits/iteration
• Caution:  False indications of chaos
• Unbounded orbits can have l₁ > 0
• Orbits can separate but not exponentially
• Can have transient chaos

Lyapunov Exponent for 1-D Maps

• Suppose  X_n+1 = f(X_n)
• Consider a nearby point X_n + dX_n
• Taylor expand:  dX_n+1 = df/dX dX_n + ...
• Define e^l = |dX_n+1/dX_n| = |df/dX|  (local Lyapunov number)
• Local Lyapunov exponent:  l = log |df/dX|
• Can use any base such as log_e (ln) or log₂
• Since df/dX is usually not constant over the orbit,
• We average <log |df/dX|> over many iterations
• For example, logistic map:
• df/dX = A(1 - 2X), and
• log |df/dX| is minus infinity at X = 1/2
• l(A) has a complicated shape
• There are infinitely many negative spikes
• A = 4 gives l = ln(2)  (or 1 bit per iteration)

Lyapunov Exponents for 2-D Maps

• Suppose  X_n+1 = f(X_n, Y_n), Y_n+1 = g(X_n, Y_n)
• Area expansion:  A_n+1 = A_ne^l1^+l2  (as with eigenvalues)
• l₁ + l₂ = <log (A_n+1/A_n)> = <log |det J|> = <log |f_xg_y - f_yg_x|>
• For example, Hénon map:
• X_n+1 = 1 - CX_n² + BY_n   [= f(X, Y)]
• Y_n+1 = X_n   [= g(X, Y)]
• Alternate representation:  X_n+1 = 1 - CX_n² + BX_n-1
• Note: This reduces to quadratic map for B = 0
• Usual parameters for chaos: B = 0.3, C = 1.4
• l₁ + l₂ = <log |f_xg_y - f_yg_x|> = log |-B| = -1.204 (base-e)

(or -1.737 bits per iteration in base-2)
• Contraction is the same everywhere (unusual)
• Numerical calculation gives l₁ = 0.419 (base-e)

(or 0.605 bits per iteration in base-2)
• Hence l₂ = -1.204 - 0.419 = -1.623 (base-e)

(or -2.342 bits per iteration in base-2)

Lyapunov Exponents for 3-D Flows

• Sum of LEs:  Sl = l₁ + l₂ + l₃ = <trace J> = <f_x + g_y + h_z>
• Must be negative for an attractor (dissipative system)
• This is the divergence of the flow
• It is the fractional rate of volume expansion (or contraction)
• For a conservative (Hamiltonian) system, sum is zero
• For non-point attractors, one exponent must = 0

[corresponding to the direction of the flow]
• For a chaotic system, one exponent must be positive

Numerical Calculation of Largest Lyapunov Exponent

1. Start with any initial condition in the basin of attraction
2. Iterate until the orbit is on the attractor
3. Select (almost any) nearby point (separated by d₀)
4. Advance both orbits one iteration and calculate new separation d₁
5. Evaluate log |d₁/d₀| in any convenient base
6. Readjust one orbit so its separation is d₀ in same direction as d₁
7. Repeat steps 4-6 many times and calculate average of step 5
8. The largest Lyapunov exponent is l₁ = <log |d₁/d₀|>
9. If map approximates an ODE, then l₁ = <log |d₁/d₀|> / h
10. A positive value of l₁ indicates chaos

General character of exponents in 3-D flows:

 

l1	l2	l3	Attractor
neg	neg	neg	equilibrium point
0	neg	neg	limit cycle
0	0	neg	2-torus
pos	0	neg	strange (chaotic)

• For flows in dimension higher than 3:
• (0, 0, 0, -, ...)  3-torus, etc.
• (+, +, 0, -, ...)  hyperchaos, etc.

Kaplan-Yorke (Lyapunov) Dimension

• Attractor dimension is a geometrical measure of complexity
• Random noise is infinite dimensional (infinitely complex)
• How do we calculate the dimension of an attractor?  (many ways)
• Suppose system has dimension N  (hence N Lyapunov exponents)
• Suppose the first D of these sum to zero
• Then the attractor would have dimension D

(in D dimensions there would be neither expansion nor contraction)
• In general, find the largest D for which l₁ + l₂ + ... + l_D > 0

(The integer D is sometimes called the topological dimension)
• The attractor dimension would be between D and D + 1
• However, we can do better by interpolating:

D_KY = D + (l₁ + l₂ + ... + l_D) / |l_D+1|
• The Kaplan-Yorke conjecture is that D_KY agrees with other methods
• Multipoint interpolation doesn't work
• 2-D Map Example: Hénon map  (B = 0.3, C = 1.4)
• l₁ = 0.419 and l₂ = -1.623
• D = 1 and D_KY = 1 + l₁ / |l₂| = 1 + 0.419 / 1.623 = 1.258
• Agrees with intuition and other calculations
• 3-D Flow Example:  Lorenz Attractor  (p = 10, r = 28,  b = 8/3)
• Numerical calculation gives l₁ = 0.906
• Since it is a flow, l₂ = 0
• l₁ + l₂ + l₃ = <f_x + g_y + h_z> = -p - 1 - b = -13.667
• Therefore, l₃ = -14.572
• D = 2 and D_KY = 2 + l₁ / |l₃| = 2 + 0.906 / 14.572 = 2.062
• Chaotic flows always have D_KY > 2

[Chaotic maps can have any dimension]

Precautions

• Be sure orbit is bounded and looks chaotic
• Be sure orbit has adequately sampled the attractor
• Watch for contraction to zero within machine precision
• Test with different initial conditions, step size, etc.
• Supplement with other tests (Poincaré section, Power spectrum, etc.)