Energetics of Walking
and Running
J. C. Sprott
Also available is MS-Word
format
Introduction
What follows is an estimate of the power
consumed in walking and in running as a function of a person's
mass (m), leg length (L), and running speed (v).
The speed at which running becomes more efficient than walking
is calculated. An estimate is given for the maximum sustained
running speed. The minimum required coefficient of friction is
calculated for walking and running.
Walking Model
Make the following assumptions about the
walking process:
1) Each leg is stiff during the time of its
contact with the ground like the spokes of a wheel, which
thereby rotates without benefit of a rim, and thus each foot
leaves contact with the ground at the instant the other touches
the ground. The flexing of the knee of the free leg serves only
to keep that foot from contacting the ground as its leg swings
forward, and such flexure doesn't consume significant energy or
change the natural period of oscillation of the leg.
2) The legs swing with their natural period,
assumed to be given by T = 2p [2L / 3g]1/2,
where g = 9.8 m/s2 is the acceleration due to
gravity and p = 3.14 (pi), independent of walking speed.
3) Energy is consumed in raising the center of
mass of the body once per step, and this energy is not recovered
when the center of mass is lowered again.
Under these assumptions, it is straightforward
to calculate the power (energy per unit time) expended in
walking:
Pw = (mg / p) [3gL /
2]1/2{1 - [1 - p2v2 / 6gL]1/2}
Running Model
Make the following assumptions about the
running process:
1) Each foot contacts the ground for a
negligible time during which an impulsive force propels the body
along a parabolic trajectory until the opposite foot strikes the
ground.
2) The upward component of the velocity of the
center of mass of the body at the instant the foot leaves the
ground is equal to the horizontal velocity of the center of mass
so as to achieve maximum range before the opposite foot strikes
the ground.
3) Energy is consumed in raising the center of
mass of the body once per step, and this energy is not recovered
when the center of mass is lowered again.
Under these assumptions, it is straightforward
to calculate the power (energy per unit time) expended in
running:
Pr = mgv / 4
Numerical Example
As a specific example, and to see if the
models are reasonable, calculate the power consumed for walking
and running as a function of speed v for an individual
with m = 100 kg and L = 1 m. The results are
shown in Fig. 1. The powers increase with speed--linearly for
running, and quadratically for walking at low speed. The powers
consumed in walking and running are similar at a speed of about
2 m/s (about 4.5 miles per hour), and are about 500 Watts for
our 100 kg (220 pound) person. These values seem reasonable.
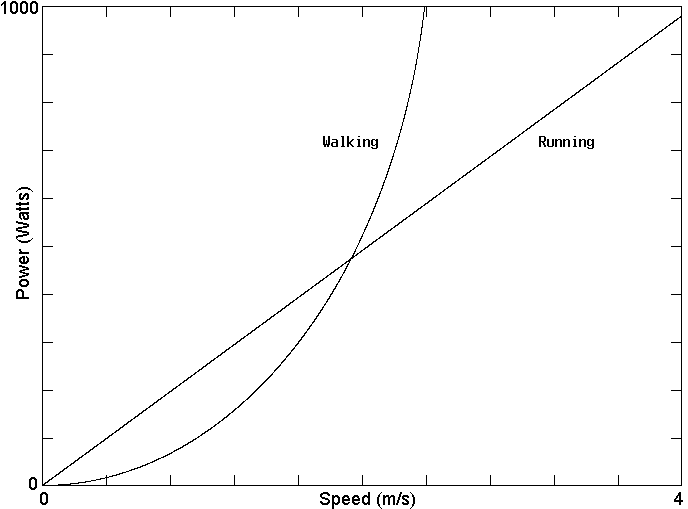
Figure 1. The power required to walk and to
run at various speeds. Note that below a speed of about 2 m/s,
it is more efficient to walk than to run, but above that
speed, it is more efficient to run.
Transition Speed
It is easy to calculate the speed vc
above which running consumes less power than walking at the same
speed. This is done by equating Pw to Pr
and solving for v. The result is
vc = (12 / 5p) [2gL /
3]1/2
This critical speed depends only on the length
of the leg, and the dependence is weak (square root). The
prediction is that a shorter person will begin running at a
lower speed than will a tall person, as expected. At the
critical speed, the person advances forward by 8L / 5
with each step, which seems a bit large.
Note that on the moon where g is about
one sixth of its value on the earth, the transition speed is
about 2.5 times lower, and thus astronauts would be expected to
run even when moving rather slowly, as seems to be the case. The
result is independent of the mass of the person, and thus the
bulky equipment carried by the astronauts should not alter the
results. This prediction could be tested on a treadmill by
having the subject carry a heavy backpack.
Maximum Running Speed
As the running speed increases, the legs have
to oscillate more rapidly. It is extremely difficult to force
them to oscillate faster than their natural resonant frequency.
Additional energy, so far neglected, has to be expended to do
so. If we take this resonant frequency as the upper limit of
comfortable running, the maximum running speed vm
can be calculated:
vm = p[gL / 6]1/2
The prediction is that tall people can run
faster than short people, and that a person with legs 1 m long
should have a maximum speed of 4.02 m/s (or 8.98 miles per
hour). Sprinters can do somewhat better than this speed, but it
is a reasonable upper limit for a marathon runner.
Friction Requirements
Experience suggests that it is harder to run
on ice than to walk on ice. We can quantify this expectation by
calculating the minimum coefficient of friction m for which the foot
does not slip for each case. For the walking case, the result is
µ = v /
[6gL / p2 -
v2]
For the running case, the force is impulsive (it occurs over a
very short time interval), and it is thus much larger than the
person's weight. Furthermore, to launch the person at a 45° angle
requires equal vertical and horizontal forces. Running thus
requires µ = 1
independent of speed.
The minimum coefficients of friction required
for walking and running are shown in Fig. 2. As expected, the
minimum required coefficient of friction occurs for slow
walking. However, above a speed of v = [3gL]1/2
/ p
= 0.884 vc, it should be easier to run on ice
than to walk.
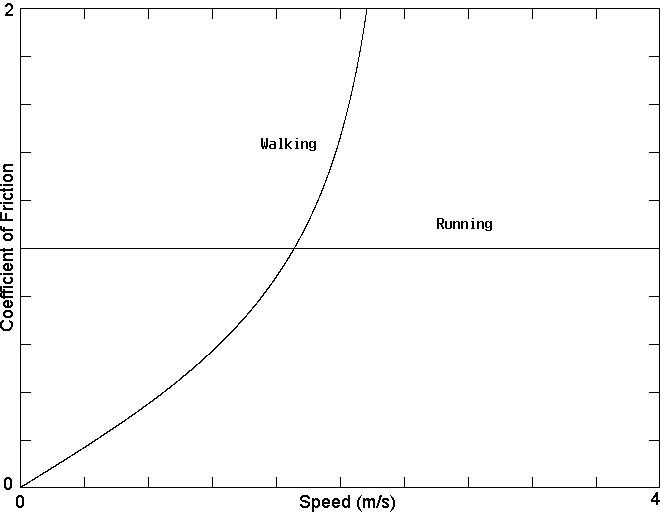
Figure 2. The minimum coefficient of
friction µ required to walk and to run. Note that below a
speed of about 2 m/s, it is easier to walk on a slippery
surface than to run, but that above that speed it is easier to
run, although the minimum coefficient of friction is µ = 1.

