Department of Physics, University of Wisconsin, Madison, WI 53706, USA
July 21, 2013
For the parameters usually studied, the Lorenz system,
x' = s(y - x)
y' = -xz + rx - y
z' = xy - bz
has a single global strange attractor. However, there is a small region of parameter space,
s = 10
24.06 < r < 24.74
b = 8/3
where the strange attractor coexists with two stable equilibria. This is mentioned in Strogatz, Nonlinear Dynamics and Chaos (1994), pp. 330-331, who references Sparrow, The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors (1982) for more detail. The purpose of this note is to show what the basins of attraction for the three attractors look like for r = 24.4.
Since the basins are three-dimensional, they are shown here in two-dimensional cross sections. The first plot shows a cross section in the plane z = 23.4 which contains the two stable equilibrium points, indicated by solid black circles and their corresponding basins of attraction in green and yellow with the basin for the strange attractor in light blue. The black lines in the blue region are a cross section of the strange attractor.
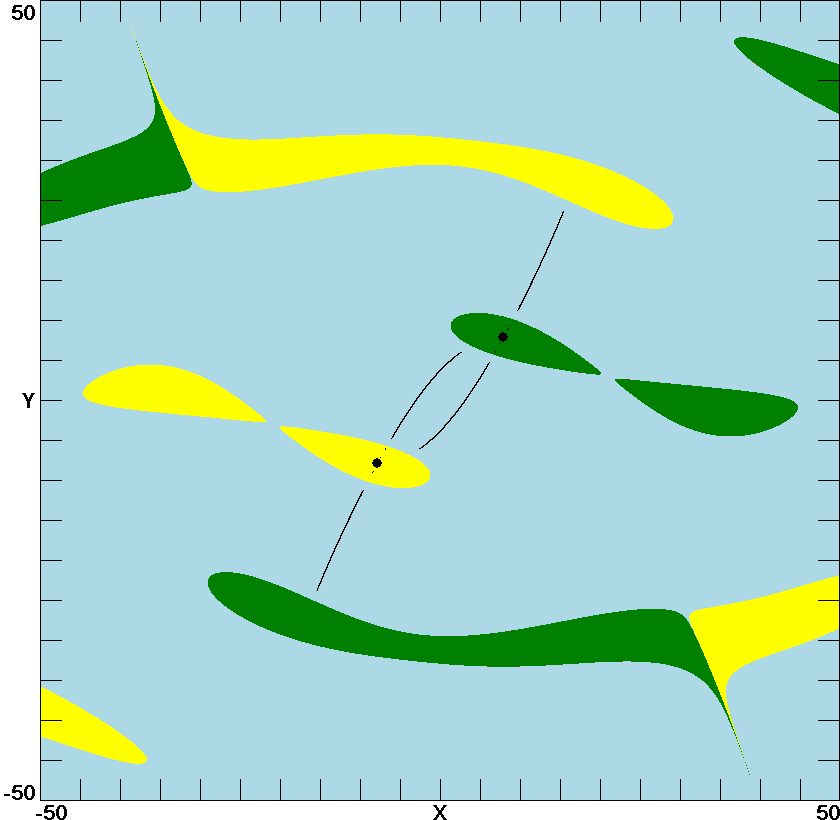
Basins of attraction for the Lorenz system
with r = 24.4 in the plane z = 23.4
Since the above cross section does not contain the unstable equilibrium at the origin, the following plot show the basins in the x=y plane where all three equilibria lie, with the unstable one indicated by an open circle. Any resemblance to a smiley face is coincidental.
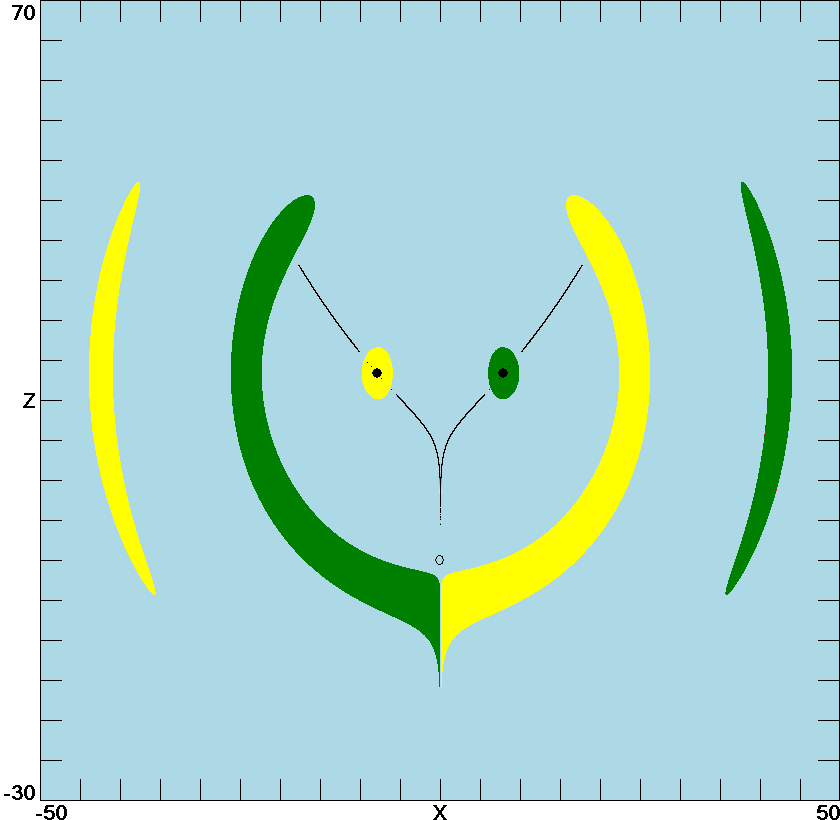
Basins of attraction for the Lorenz system with r = 24.4 in the plane x=y
Since the above cross section does not contain the unstable equilibrium at the origin, the following plot show the basins in the x=y plane where all three equilibria lie, with the unstable one indicated by an open circle. Any resemblance to a smiley face is coincidental.

Basins of attraction for the Lorenz system with r = 24.4 in the plane x=y