A RIGOROUS DETERMINATION OF THE OVERALL PERIOD IN THE
STRUCTURE OF A CHAOTIC ATTRACTOR
ZERAOULIA ELHADJ
Department of Mathematics,
University of T´eb´essa, (12000), Algeria
zeraoulia@mail.univ-tebessa.dz
zelhadj12@yahoo.fr
J. C. SPROTT
Department of Physics, University of Wisconsin,
Madison, WI 53706, USA
sprott@physics.wisc.edu
Received January 28, 2012; Revised July 12, 2012
ABSTRACT
There are many examples of
nonconnected chaotic attractors consisting of several
components. The determination of an overall period of such a
system is typically done only by a numerical integration of the
system. In this letter, we provide a rigorous proof that the
exact value of the overall period of a particular 2-D chaotic
attractor from an iterated map is two once the attractor has
partitioned and quantized into disconnected sets. As far as we
know, there are no examples of a rigorous proof for such a
property in the current literature.
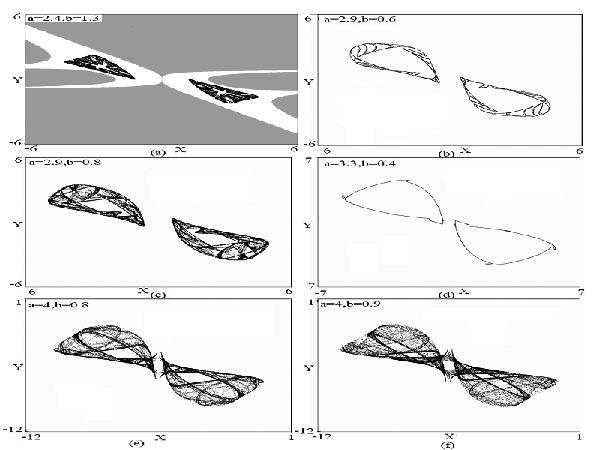
Fig. 1. Attractors of the map (1) with (a)
a = 2.4,
b
= 1.3, (b)
a = 2.9,
b = 0.6, (c)
a = 2.9,
b = 0.8, (d)
a = 3.3,
b = 0.4, (e)
a
= 4,
b = 0.8, (f)
a = 4,
b = 0.9. From
[Zeraoulia & Sprott, 2011]

