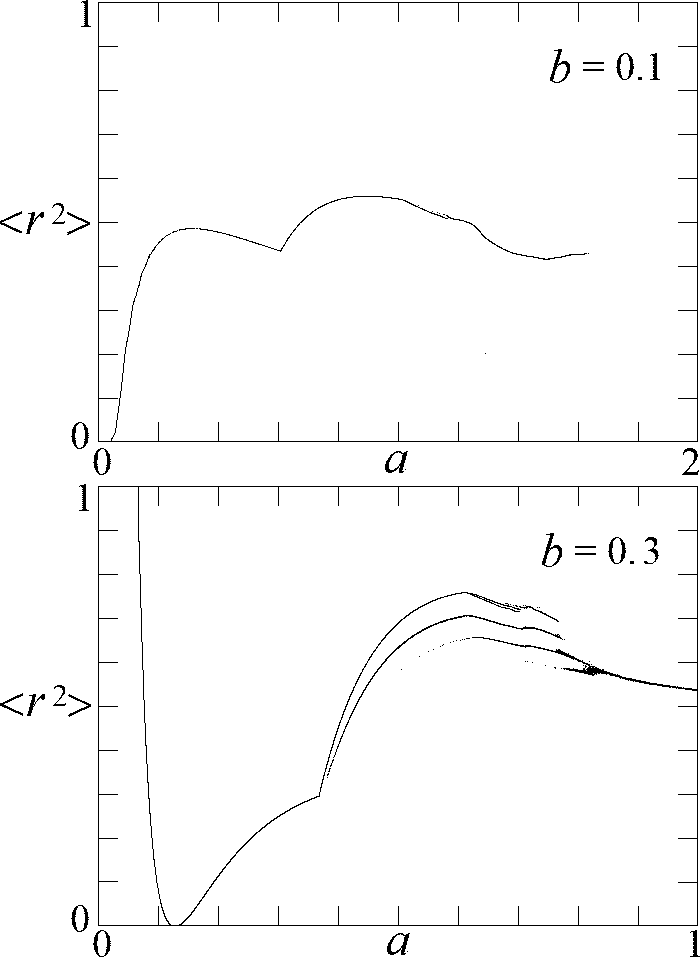High-Dimensional Dynamics in the Delayed Henon Map

J. C. Sprott
Departments of Physics, University of Wisconsin, Madison, WI 53706, USA

Received 3 April 2006, Accepted 16 August 2006, Published 20 September 2006

ABSTRACT

A variant of the Henon map is described in which the linear term is replaced by one that involves a much earlier iterate of the map. By varying the time delay, this map can be used to explore the transition from low-dimensional to high-dimensional dynamics in a chaotic system with minimal algebraic complexity, including a detailed comparison of the Kaplan-Yorke and correlation dimensions. The high-dimensional limit exhibits universal features that may characterize a wide range of complex systems including the spawning of multiple coexisting attractors near the onset of chaos.

Ref: J. C. Sprott, Electronic Journal of Theoretical Physics 3, 19-35 (2006)

The complete paper is available in PDF format.

Return to Sprott's Books and Publications.


Fig. 1. Regions of dynamical behaviors for Eq. (1) for various values of the time delay.
Fig. 1.

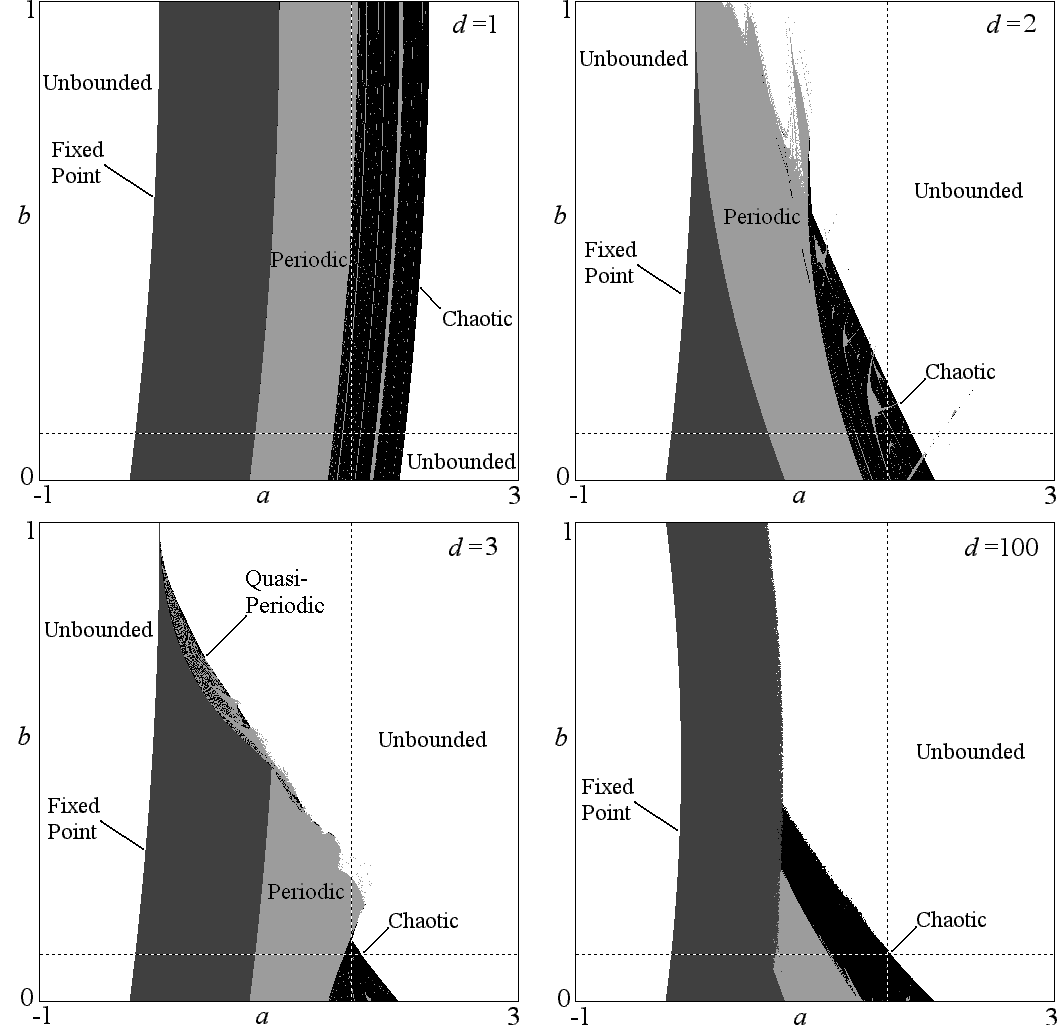
Fig. 2. Attractors for the system in Eq. (1) with a = 1.6 and b = 0.1 for various values of the time delay.
Fig. 2.


Fig. 3. Kaplan-Yorke dimension and Lyapunov exponents for the system in Eq. (1) with a = 1.6 and b = 0.1 versus time delay.
Fig. 3.


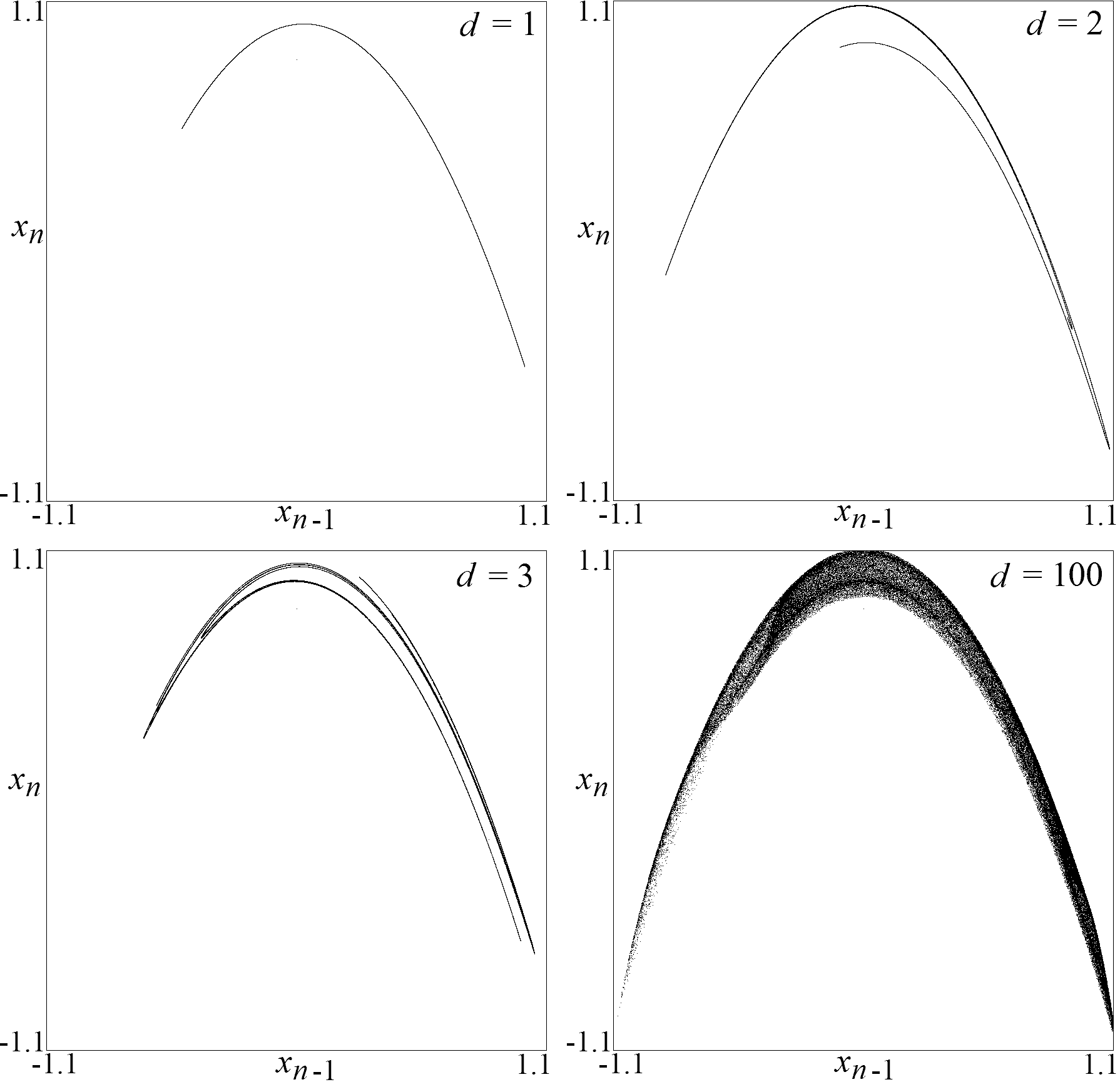
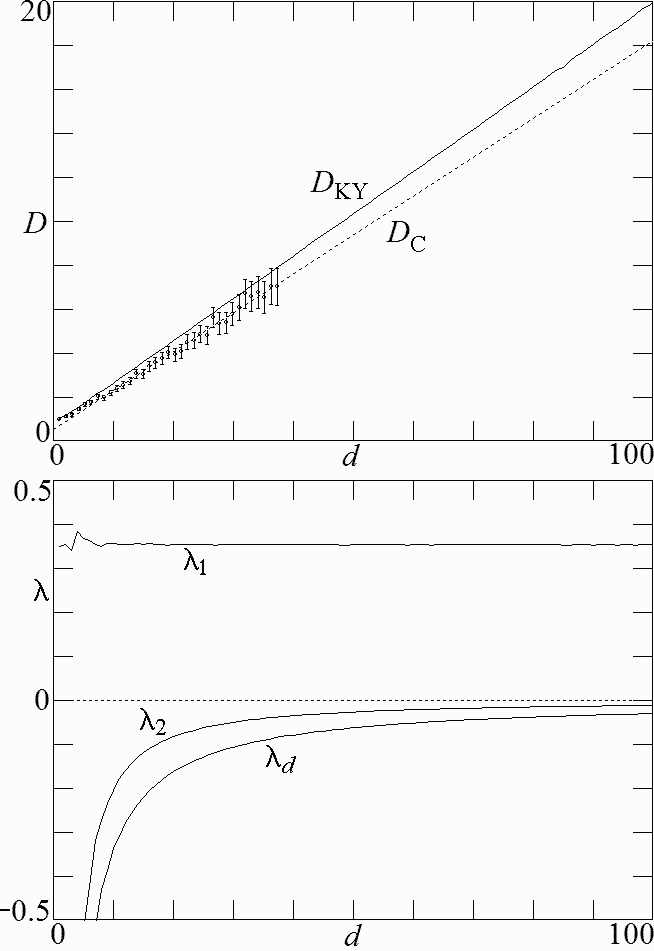
Fig. 4. Kaplan-Yorke dimension and Lyapunov exponents for the system in Eq. (1) with b = 0.1 showing the route to chaos at low dimension (d = 2) and high dimension (d = 100).
Fig. 4.

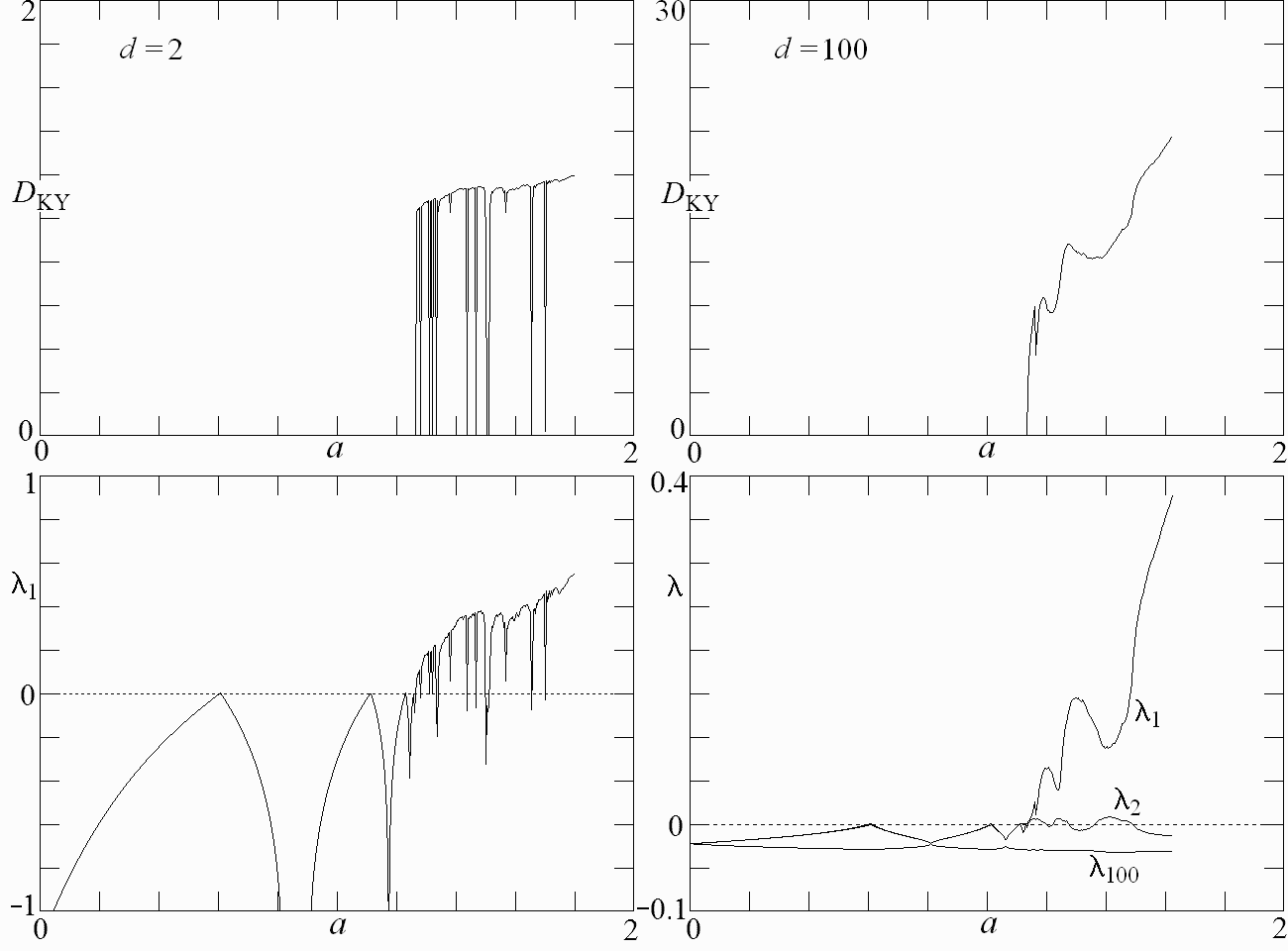
Fig. 5. Kaplan-Yorke dimension and a few of the largest Lyapunov exponents for the system in Eq. (1) with b = 0.1 and d = 100 showing in more detail the onset of chaos.
Fig. 5.

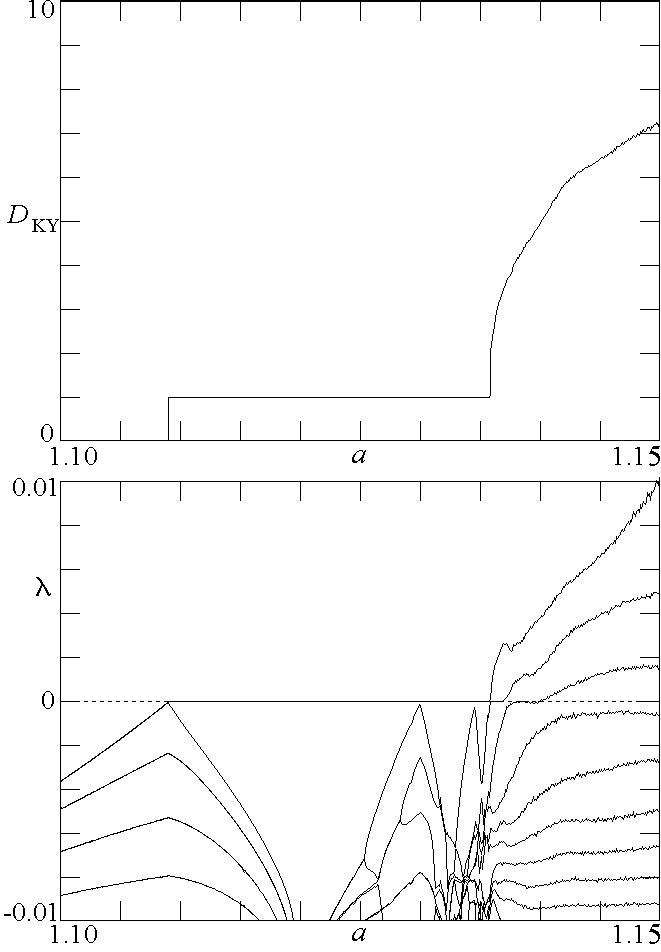
Fig. 6. Attractors for the system in Eq. (1) with b = 0.1 and d = 100 showing period doubling of a drift ring approaching the onset of chaos.
Fig. 6.

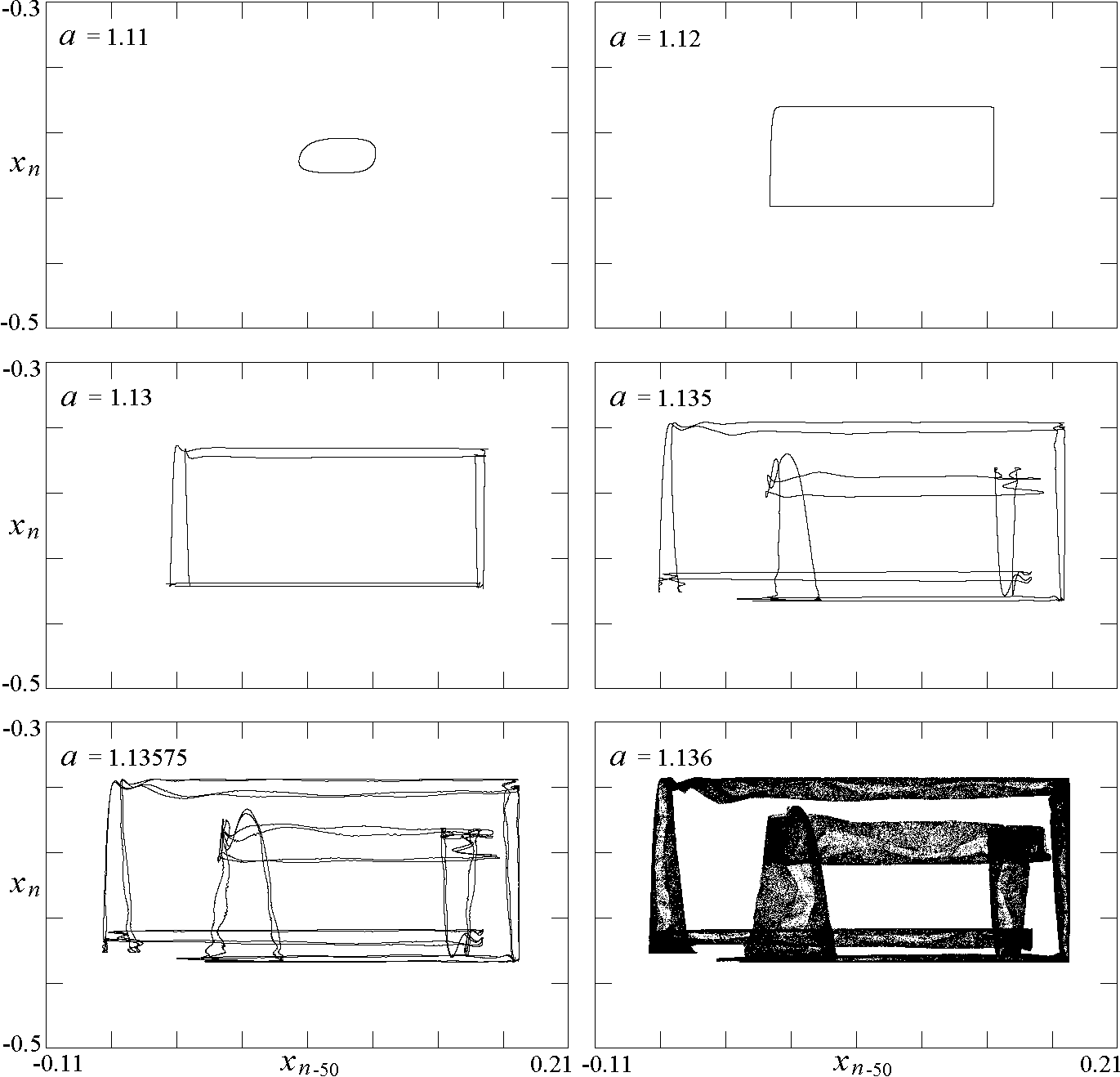
Fig. 7. Global bifurcations and multiple attractors for two values of b with d = 100.
Fig. 7.

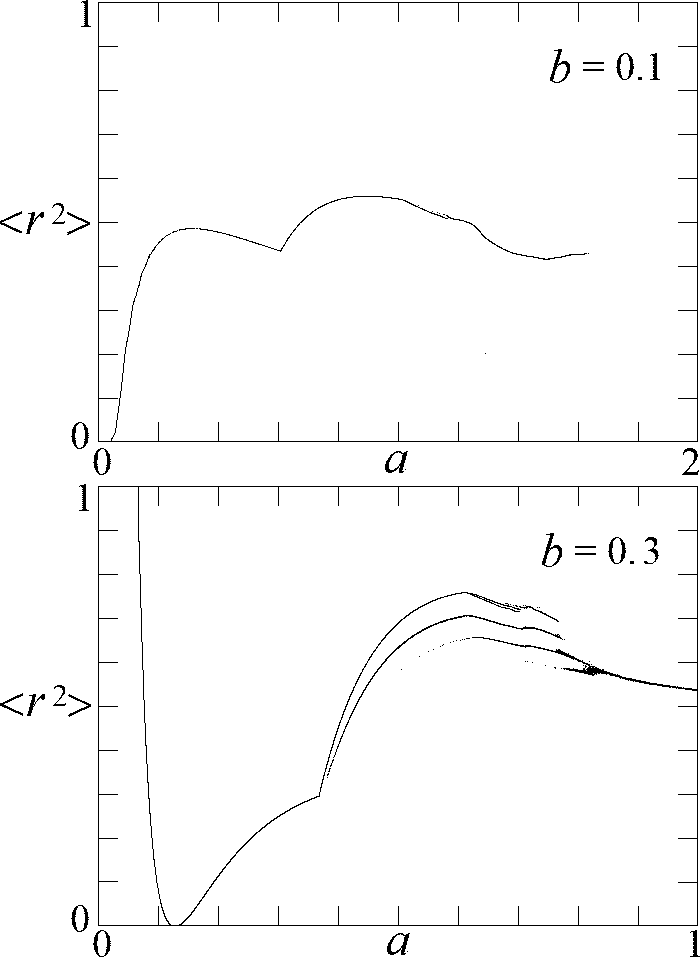
Fig. 8. Relative probability of different values of <r2> for a = 0.7, b = 0.3, and d = 100, indicating the existence of at least seven distinct attractors.
Fig. 8.

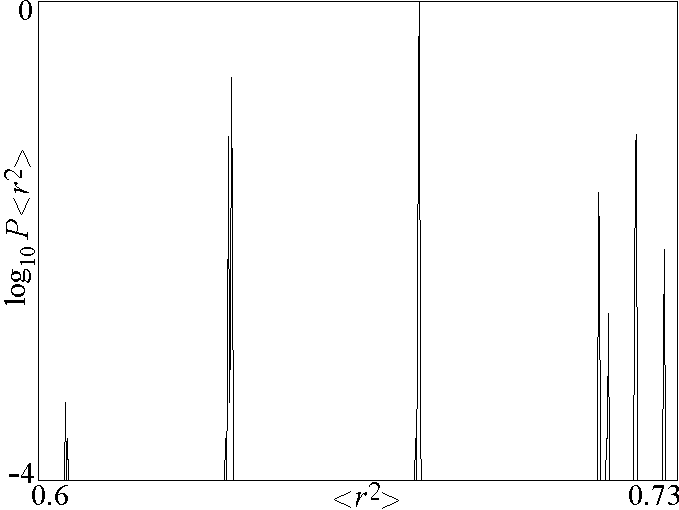
Fig. 9. Four coexisting attractors for a = 0.7, b = 0.3, and d = 100 near the onset of chaos.
Fig. 9.