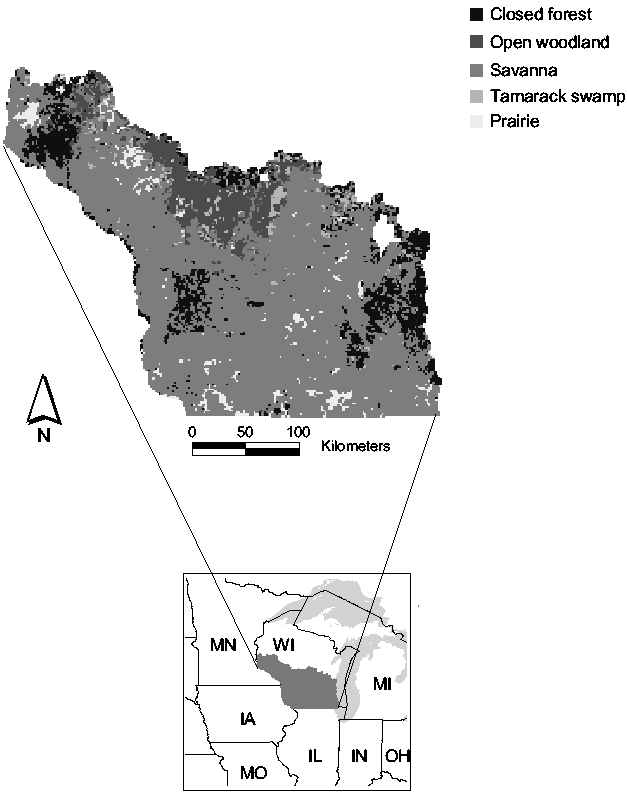
Fig. 1: The historical landscape of southern Wisconsin, USA
A case study for self-organized criticality and complexity in forest landscape ecology
Janine Bolliger
Swiss Federal Research Institute (WSL)
Zürcherstrasse 111; CH-8903 Birmendsdorf, Switzerland
janine.bolliger@wsl.ch
1.1 Introduction
Current challenges in ecological research aim at relating the understanding of individual plant or animal landscapes to higher-level phenomena that can be approximated by general concepts. Since self-organized criticality is a very universal phenomenon occurring across a broad range of disciplines, it may serve as a tool to address the understanding of ecosystem complexity and function in a more general framework. The phenomenon of self-organized criticality is thus a powerful interdisciplinary approach for completion of some of the current theoretical frameworks (e.g., metapopulation theory, static equilibrium theory) with a profound understanding of how ecological feedback (e.g., resource limitations), internal interactions (e.g., selection, competition), or historical accident act together in order to understand how and why biotic units occur together on their current locations across ecosystems. The successes of physics give confidence that models using simple parameters can account for the general behavior of system complexity. This may be unlikely applied to ecology, where details in their spatio-temporal context often matter. However, critical phenomena are a field where the intuitive idea that large amounts of detail are needed to explain the observed complexity, does not hold true. Simple models, thus, have been successfully used in a variety of ecological fields to address theoretical as well as applied fields in ecology.
In this paper, we investigated the historical landscape of southern Wisconsin (60,000 km2) for self-organized criticality and complexity. The landscape is patterned into prairies, savannas, open and closed forests, using data from the United States General Land Office Surveys that were conducted during the 19th century, at a time prior to Euro-American settlement.
A simple cellular automaton replicates the fractal pattern of the forest landscape and predicts its evolution. Spatial distributions and temporal fluctuations in global quantities show power-law spectra, implying scale-invariance, characteristic of self-organized criticality. The evolution toward the self-organized critical state and the robustness of that state to perturbations are discussed.
1.2 The historical forest landscape of southern Wisconsin
The study area covers approximately 60,000 km2 and includes the southern part of the state of Wisconsin, USA. The historical landscape of southern Wisconsin is represented by the United States General Land Office Surveys. The surveys are widely recognized to provide a good basis for large-scale quantitative and qualtitative information on landscapes prior to Euro-American settlement, albeit of various biases and constraints (Manies and Mladenoff 2000; Bolliger et al., 2002; Mladenoff et al., 2002). In Wisconsin, the surveys were conducted between 1832 and 1866. The land was divided into township grids, each consisting of 36 1-mile (1.6 x 1.6 km) sections. Survey posts were set every half a mile (quarter section corners), and every full mile (section corners). Typically, one to four trees near the posts were blazed (witness trees) to mark the section and quarter section corners. The witness tree species, diameter, and distance to the corner were recorded. Descriptive notes on ecosystem properties such as swamps, burns, or windfall were recorded, and occasionally sketched. The set of original field notes was digitally compiled for the entire state of Wisconsin for the purpose of ecological analysis and mapping purposes (Sickley, 2000). We used tree-species information of all types of corners (section, quarter section, line, and meander corners) to conduct this study.
Prior to Euro-American settlement, the landscape of southern Wisconsin consisted of primarily four major vegetation types: prairies, savannas, open and closed woodlands. The tree densities derived from the surveys were used to distinguish landscape patterns according to a classification by Anderson and Anderson (1975): Prairie (<0.5 trees/ha), savanna (0.5-46 trees/ha), open woodland (46-99 trees/ha), and closed forest (> 99 trees/ha) (1 ha = 1 x 104 m2). Pixels dominated by tamaracks were categorized as swamps.
The historical landscape of southern Wisconsin was dominated by savannas, followed by forests and prairie. Tamarack swamps are very rare (Fig. 1).

Fig. 1: The historical landscape of southern Wisconsin, USA
1.3 The cellular automaton model
The cellular automaton model consists of a rectangular array of 253 x 202 cells. Each cell has one of six values (representing prairie, savanna, open or closed forest, tamarack swamp, or missing data) chosen with the same probability as the data since for calculations longer than a few thousand generations, there is a tendency for the minority categories to become extinct. To prevent that from happening, the replacements are made with a probability slightly less than 100% that is continually adjusted to keep the probability of each category approximately constant. In doing so, we assume that the proportions of the landscape pattern stays constant through time, i.e., the environmental constraints that shape the landscape (fire, wind) do not change through time. At each time step, landscape evolution is driven by a randomly chosen cell in the array that is replaced by a cell chosen randomly from its circular neighborhood of radius r (measured in units of the cell size) where r is the only parameter of the model measured in units of the lattice spacing. The radius r may take values between 1 (local) and 10 (regional) units. The r = 1 unit case includes 4; the r = 3 case includes 28, and the r = 10 case includes 314 grid cells.
The model’s robustness was tested for initial conditions (random and ordered), boundary conditions (periodic and reflecting) and perturbation experiments. Perturbations are generated by varying the initial proportions of the landscape pattern and by cells that are randomly assigned different landscape types. Dying perturbations (i.e., decrease in perturbed cells) indicate low sensitivity to the initial conditions, whereas growing perturbations (i.e., increase in perturbed cells) over time indicate strong sensitivity. The model’s sensitivity to the original 1-square mile grid size was tested by resampling the grid on various grid sizes ranging from 2 to 8 miles. All results presented here are not sensitive to any of the measures of robustness.
1.4 Measures of self-organized criticality and complexity
1.4.1 Fractal dimension and spatial scale-invariance
Fractal geometry is used to compare properties of the spatial structures of simulated and observed landscapes since they quantify the spatial complexity apparent in landscapes. Here, we applied a variant of the Grassberger-Procaccia algorithm (Grassberger and Procaccia 1983) to quantify the total structure of the landscape (Sprott et al. 2002). The fractal dimension is calculated using correlation sums. The correlation sum C(r) is defined as the probability that two randomly chosen points of the same landscape type are within a distance e of one another, where e is taken as the maximum norm |x1 – x2| + |y1 – y2|. To assess the pattern-size scale invariance, the log of the correlation sum C(e ) is plotted versus the log of the scale size e . The range of e over which the plot is a straight line is the scaling region, and the slope of the line dlogC(e )/dloge is the correlation dimension, which is one measure of the fractal dimension and a point of comparison of the model with the observations. Power laws are usually referred to as a footprint of self-organization to a critical state. In a spatial context, this indicates that the landscape exhibits the highest pattern diversity, dominated by few large, and many smaller patterns. Changes in pattern size affect the entire pattern distribution across all scales.
Results show that the fractal dimension (slope of the graph) for both the observed and simulated landscape is about 1.6, indicating that the spatial properties of the observed landscape are well reproduced by the model (Fig. 2). The slope remains constant, indicating that no particular spatial scale is singled out, and that a pattern has the same properties when observed at different spatial resolutions. This property is referred to as spatial scale invariance, meaning that the landscape is a true fractal.
1.4.2 Cluster probability and temporal scale-invariance (1/f power laws)
Cluster probability is used to measure organization and the temporal behavior of the simulated landscape. It is defined as the portion of cells that are part of a cluster on the entire array of cells. A point in the array is assumed to be part of a cluster if its four nearest neighbors are the same as it is. A highly disorganized array has a small cluster probability, and a highly organized array has a large cluster probability. The cluster probability i.e., the portion of cells that are part of a cluster across the entire region amounts to 32.3% for the observed landscape (Fig. 3). Cluster probability was used to assess the temporal scale-invariance as evidenced by 1/f temporal fluctuations in power spectra. 1/f power spectra typically contain a large amount of both, high frequency and low frequency signals with no characteristic time scale. The measure for organization of the landscape, cluster probability, approaches 32.3% for the observed landscape (Fig. 3) indicating that 32.3% of the cells are part of clusters that ultimately form the observed landscape pattern in Fig. 1.

Fig. 2: Fractal dimension as a measure of comparison between obsered and simulated landscape pattern

Fig. 3: Cluster probability as a measure of comparison between observed and simulated landscape patterns. The landscape evolves with (a) random, (b) ordered initial conditions
The different sizes of neighborhoods (radius sizes) used in the model can be viewed as a measure of how far away cells are able to interact with each other. Choosing small neighborhoods (r = 1 that corresponds to 4 neighboring cells), results in over-organization of the landscape (Fig. 3) i.e., it reaches a higher percentage of clustered cells (68.9%) than the observed landscape (32.3%). As cells within a small neighborhood are more likely to exhibit similar features, and since local interactions due to small radii sizes allow only limited connection with the entire set of features occurring on the landscape, it is more likely that evolving cells find cells with the same features, and thus over-organize. If large neighborhoods (r = 10 that corresponds to about 314 neighboring cells) are chosen, the simulated landscape does not self-organize, exhibiting a cluster probability less than 10% (Fig. 3 (a) and (b)). Large neighborhoods account for the overall landscape-pattern diversity. In such cases the likelihood that cells with identical properties interact is small since such cells are often found adjacent to each other. If intermediate neighborhoods (r = 3 that corresponds to about 28 neighboring cells) are chosen, however, self-organization of the landscape to the observed value of 32.3% is observed (Fig. 3 (a) and (b)). Intermediate neighborhood sizes appear thus to account for large enough landscape diversity to allow occasional larger-distance interactions, in addition to the small-scale interactions between neighbors. The effect of the neighborhood sizes on self-organization is independent of the initial conditions. For a completely random landscape in Fig. 3 (a), order is created (increasing cluster probability) with time. For a completely ordered landscape in Fig. 3 (b), the order is decreased (decreasing cluster probability). Analyses of the temporal fluctuations of the cluster probability after convergence for the different sizes of neighborhoods as analyzed in Fig. 3 are shown in Fig. 4. When plotted on a log-log scale, the power (squares of amplitudes) and the frequency (inverse of the period) of the converged graph of the cluster probability exhibit power-law behavior for r = 1 and r = 3 (Fig. 4 a). Power spectra that exhibit straight lines are referred to as power laws. The straight line of the power law indicates that no particular time scale is singled out, and the properties of a given frequency stand for all frequencies (scale invariance), indicating that any landscape-pattern change may take place any time and are likely to affect the entire landscape on every temporal scale. The neighborhood size of r = 10 does not show power-law behavior (Fig. 4 b), as particular time scales are singled out (i.e., the graph is not a straight line).
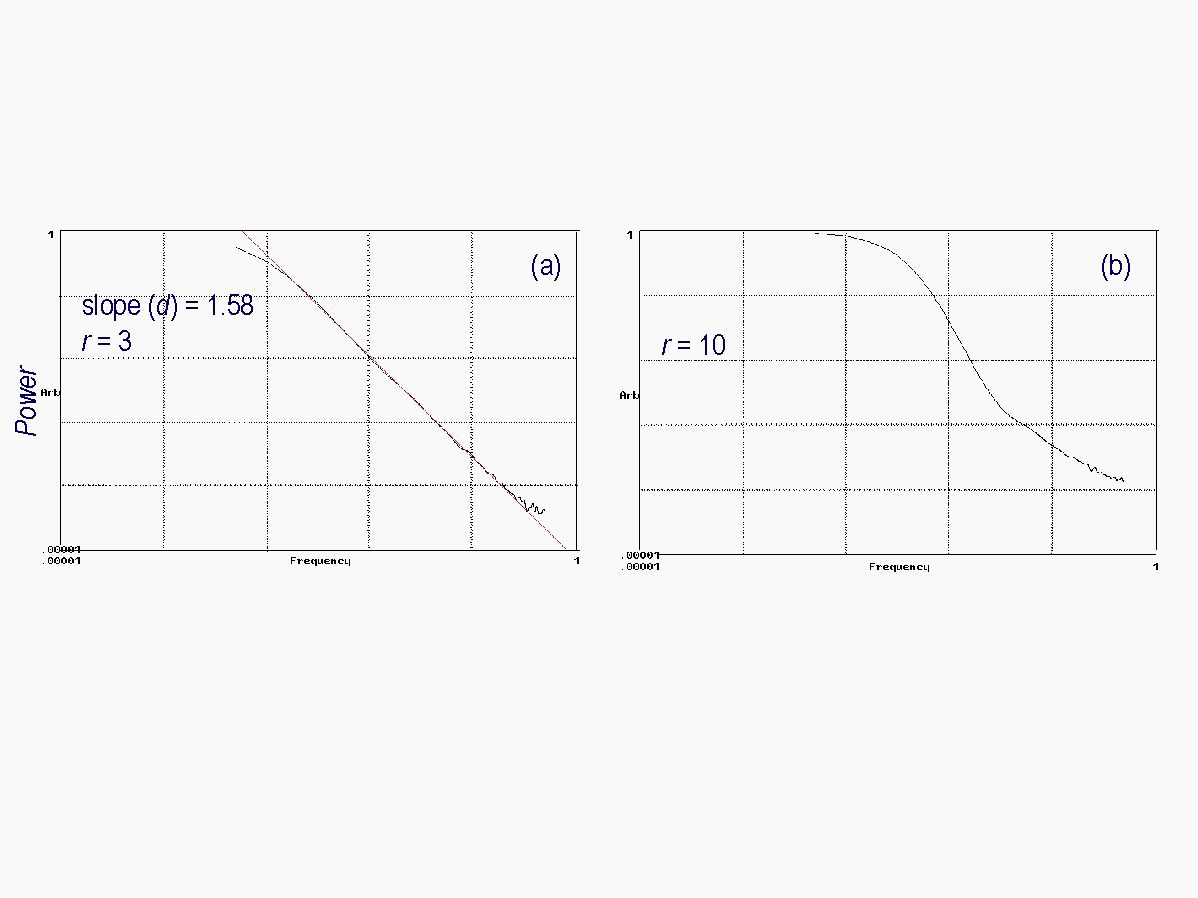
Fig. 4: (a): Power law behavior for r = 1 and r = 3 (b) no power law for r = 10
1.4.3 Algorithmic complexity
Algorithmic complexity is used as a measure of comparison between the complexity of the observed and the simulated landscapes. Algorithmic complexity is the size of the simplest computational algorithm that is able to reproduce the data. With this approach, condensation of the entire set of interactions between system components is achieved. One way to estimate this quantity takes advantage of the fact that GIF graphic files are nearly optimally compressed. The algorithmic complexity of the landscape-pattern graphics is determined by the size of the GIF file of the landscape image after substracting the fixed size of the file header (Sprott et al. 2002).
Results show that the GIF file representing the observed landscape compresses to 6205 bytes. The self-organized simulated landscape with r = 3 compresses to a size similar to the observed landscape (6792 bytes) compared to a complete random landscape that compresses to 8136 bytes.
1.5 Summary
We present a generic and process-independent model that is sufficient for generating a complex pattern resembling the historical landscape of southern Wisconsin. The model uses a single, adjustable parameter to mimick low-level interaction processes among the landscape components (patterns). Our model predicts that generic simple rules (a) may create self-organization by driving the dynamics of a landscape so that order emerges spontaneously from different initial conditions, and (b) self-organize to a critical state by presenting the dynamics as scale-free: temporally as power laws and spatially as fractals. We thus state that models with simple rules that do not specify specific processes may suffice to replicate the landscape pattern originating from complex spatial and temporal interactions. Process-independent models (neutral models) have played an important role in various fields of ecology, including applied fields: Landscape patterning, fire disturbance, effects of habitat fragmentation on birds or mammals, extinction thresholds or predictions of the effect of habitat- and land-use changes on species, but also in the field of theoretical landscape ecology where the neutral models provide generalized null models to generate patterns in the absence of specific processes with the intention to achieve statistical, rather than spatially explicit representations of the landscape under study.
1.7 Acknowledgements
I would like to thank David J. Mladenoff, Department of Forest Ecology and Management, University of Wisconsin-Madison, Madison WI, USA, for providing the U. S. General Land Office data to conduct this work. I am very grateful for the conceptual and technical support provided by J. C. Sprott, Department of Physics, University of Wisconsin-Madison, Madison WI, USA. The Swiss National Science Foundation supported this work with a grant for prospective researchers by the University of Bern, Switzerland.
1.8 References
Anderson, R. C. and M. R. Anderson. 1975. The presettlement vegetation of Williamson County, Illinois. Castanea 40:345-363.
Bolliger J., Nordheim E. V., Mladenoff D. J. 2002. A single-parameter using tree-species associations to reduce ambiguities in historical data sets. Landscape Ecology. In review.
Manies K. L., Mladenoff D. J. 2000. Testing models to produce landscape-scale presettlement vegetation maps form the U.S. public land survey records. Landscape Ecology 15: 741-754.
Manies K. L., Mladenoff D. J., Nordhein, E. V. 2001. Assessing large-scale surveyor variability in the historic forest data of the original US public land survey. Canadian Journal of Forest Research 31: 1719-1730..
Mladenoff D. J. Dahir S. E. Schulte L. A., Guntenspergen G. G. 2002. Narrowing historical uncertainty: A probabilistic classification of ambiguously identified tree species in historical forest survey data. Ecosystems. In press.
Grassberger P., Procaccia I, Phys. Rev. Lett. 50 (1983) 346.
Sickley T. A. 2000. Pre-European settlement vegetation of Wisconsin, Database documentation V. 1. April 2000. 20 pp.
Sprott J. C., Bolliger J., Mladenoff D. J. 2002. Self-organized criticality in forest landscape evolution. Physics Letters A. In press.