Contact |
Books |
Home |
Contact |
Books |
Home |
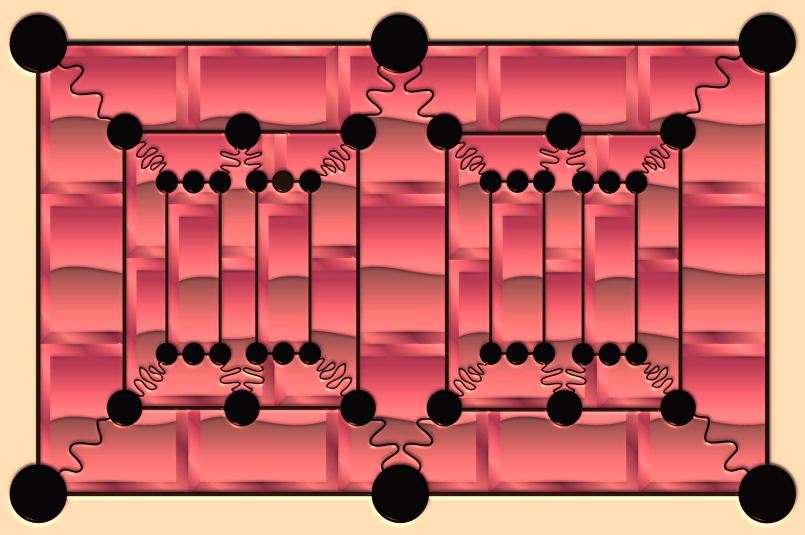
"I believe that scientific knowledge has fractal properties, that no matter how much we learn, whatever is left, however small it may seem, is just an infinitely complex as the whole was to start with. That, I think, is the secret of the Universe." - Isaac Asimov, I. AsimovThe playing board for the Fractal Fantasies is a fractal nesting of interconnected rectangles (see figure). The board contains rectangles within rectangles interconnected with wiggly lines as shown in the figure. There are always two rectangles within the rectangles which encompass them. The degree of nesting can be varied.
 Beginners play with only a few nested rectangles, while grand masters play with many recursively positioned
rectangles -- like Russian dolls within dolls within dolls. Tournaments last for days.
The playing board illustrated here is called a "degree 2" board, because it has two different sizes of rectangles within the large bounding rectangle. Beginners
usually start with a degree 1 board, and grand masters have been known to use a degree 20 board.
Beginners play with only a few nested rectangles, while grand masters play with many recursively positioned
rectangles -- like Russian dolls within dolls within dolls. Tournaments last for days.
The playing board illustrated here is called a "degree 2" board, because it has two different sizes of rectangles within the large bounding rectangle. Beginners
usually start with a degree 1 board, and grand masters have been known to use a degree 20 board.
One player uses white playing pieces (like stones), the other uses black. Each player starts with a number of pieces equal to 1/2 the number of vertices (dots) on the board minus two. For the board here, each player gets 19 stones. With alternate moves, the players begin by placing a stone at points on the black dots that are empty. As they place stones, each player attempts to form a row of three stones along any one of the horizontal sides of any rectangle. This three-in-a-row assembly of stones is called a Googol. When all the stones have been placed, players take turns moving a piece to a neighboring vacant space along one of the wiggly or straight connecting lines. When a player succeeds in forming a Googol (either during the alternate placement of pieces at the beginning of the game, or during alternate moves along lines to adjacent empty points) then the player captures any one of the opponent's pieces on the board and removes it from the board. In some versions of the game, an opposing stone cannot be taken from an opposing Googol.) A player loses when he or she no longer has any pieces or cannot make a move.
Mathematicians and philosophers will no doubt spend many years pondering a range of questions, particularly for boards with higher nesting. Computer programmers will design programs allowing the board to be magnified in different areas permitting the convenient playing at different size scales. They'll all wish they had fractal consciousnesses allowing the contemplation of all levels of the game simultaneously.
Many of our friends have spent years of their lives pondering the following questions relating to Fractal Fantasies. No one has succeeded in answering these questions for games with degree higher than 2. Various centers have been established and funded in order to answer the following research questions:
I've received numerous mail from readers who experimented with the Fractal Fantasies game. For example, Martin Stone from Temple University suggests a distributed version of the game played over the Internet. He writes, "Imagine a multi-user recursive game server dedicated to the fostering of a greater intuitive understanding of recursive structures and permutations." David Kaplan from New York University points out that the game rules for the Fractal Fantasies are similar to a medieval game called Nine Man Morris played on a different playing board. Paul Miller notes that the Fractal Fantasy Game was discussed at the Boston Chapter of MENSA. He asks, "Can pieces of a Googol move out and back (thus forming and reforming the Googol)?" He suggests that the Googol pieces be allowed to move only if there is no other legal move. Alternatively, if a player moves a piece out of a Googol, he should not be allowed to move it back into the same place on the next turn. Michael Currin from the University of Natal (South Africa) suggests that the game be adapted to allow more than two players. Finally, Brian Osman, a 15-year-old from Massachusetts, writes:
I greatly enjoyed your description of the Fractal Fantasies in the March 1993 issue of BYTE magazine. However, I point out that some of what you said is almost impossible! I've calculated the number of rectangles and "spots" for every size board, using the formula: [2^(N+1)] - 1, where N is the degree of the board. From this, one can find the number of spots by simply multiplying by 6. Once you have this number, divide by two and subtract two to find the number of stones for each player. You have stated that grand masters have been known to use boards of degree 20. I've checked my calculations repeatedly, and this would require each player start with 6,291,451 stones! Assuming each opening move (only those to place your pieces) took 2 seconds, the players wouldn't be able to move until 291.2708797 days after they started the game. Am I missing something, or are your numbers as ludicrous as they seem to me? Please don't take offense at this. I still found your article very enjoyable.