Contact |
Books |
Home |
Contact |
Books |
Home |
|
Let me tell you a secret. For years I have wanted to travel the longest straight line that traverses America. My rules for such a line were simple. The line could not pass outside America and could not go through the oceans and the Gulf of Mexico. In other words, the line had to stay inside the continental boundaries.
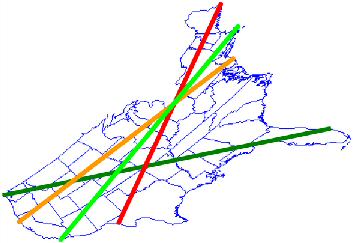
I am happy to report that my friend, Mark Nandor, has finally been able to determine the town located on both ends of such a line. Our four "test lines" are shown on the maps at right. Our early attempts involved a line that attached to Northeastern Maine, but that's the red line and clearly the best we can do is to get into West Texas, which won't give us a very long line. Similarly, the orange line from Northern. California to North Carolina doesn't cut it on the normal map, although it is much better. Going from the Southwestern tip of California up and through Cape Cod isn't so bad, but still is about 10% shorter than the dark green line that stretches from Northwestern Washington to much of the way to Southern Florida. We call this line the ultralineamentum, after the Latin word "lineamentum" [a line drawn with pen or pencil]; read more below... |
where great arcs are lines. 
|
Our journey starts at Ocean Creek by the Makah Indian Reservation in Washington, and our amazing journey ends near 1 Ocean Drive, Jupiter, Florida, 33469. (Ocean Creek is not the name of a city or town, but the name of the actual stream.)
To reiterate, our trip starts in Washington state at the beach at Ocean Creek, 124° 41' 38'' W, 48° 21' 44'' N:

Our journey ends on the beach at Jupiter, Florida at 80° 4' 29'' W, 26° 57' 11'' N:

The straight-line (on a sphere) distance between the two is 2802 miles. Mapquest (using a 200-600 foot hike at either end to actually get from the road to the ocean) tells me it would take us 52 hours and 37 minutes to get from one end to the other, and we'd have to travel 3431 miles to do it. Of course, in our real journey we would make frequent stops to enjoy the surroundings.

Accurate depiction of longest line in gnomonic coordinates:
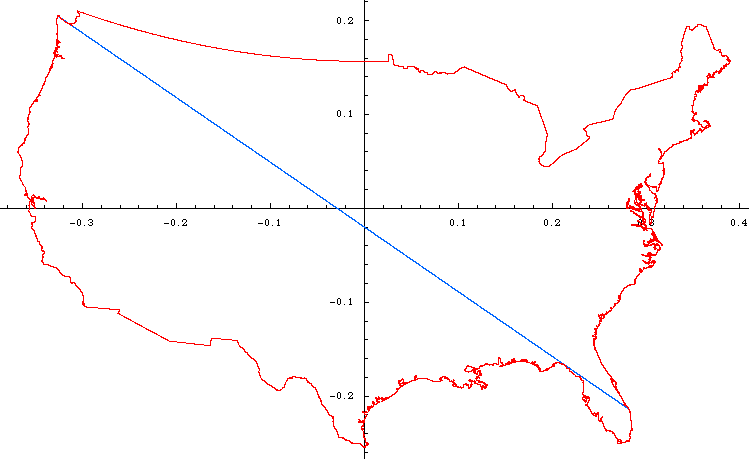
Accurate depiction of longest line in cartesian coordinates:
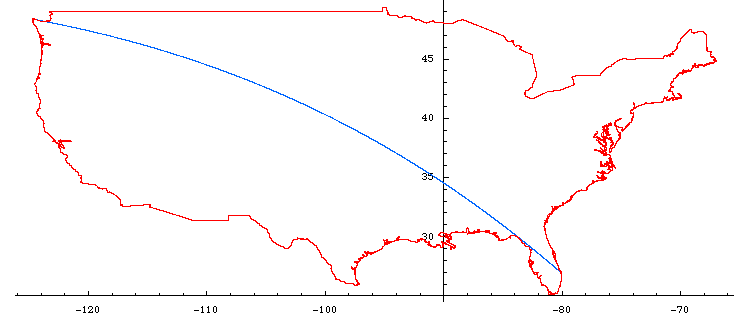
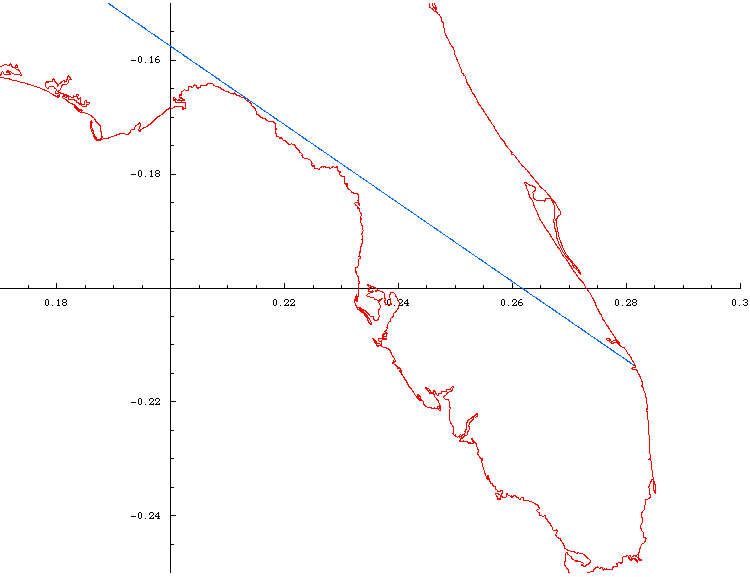
Magnification of Florida segment:
Longest line that is not all within the US:
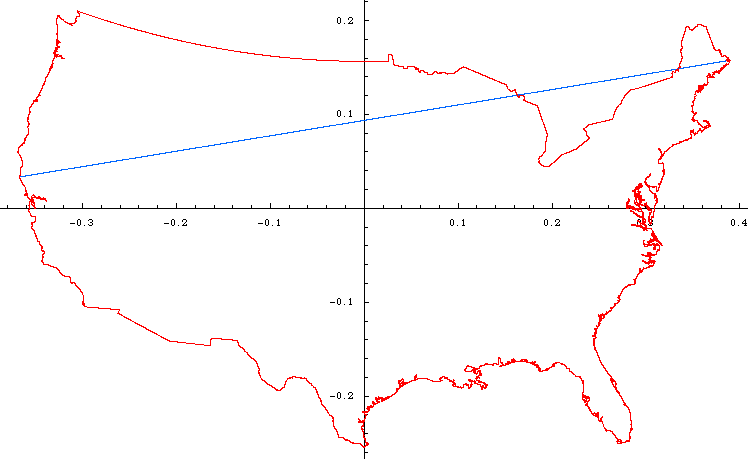
I downloaded a copy of all of the GPS landmark data from some supposed source at the CIA (http://www.evl.uic.edu/pape/data/WDB/). From this, I had to get out all of the coastline and boundary data for the United States. This actually took quite a bit of labor since they have 4 levels of "useful" data, but they don't rank them strictly as "all the 1s together" and "all the 2s together" and so on. It was actually quite annoying. But in any case, I ended up using 52332 points for the United States. The only real screwup that I ended up keeping was the US/Canada border in NW Washington as the part that goes into the Pacific, and not just the land. But I don't feel like poring through all of the coastline data to figure out which points I've left out. Those points don't matter for this case because when I ran my computer program it didn't find the longest line all the way out to the ocean, so it certainly couldn't find the longest point closer in!
In any case, I tested each pair of points to see how long the distance was on the sphere we call the Earth (yes, there are approximations involved there). If the distance was over 2700 miles, I kept that pair of points. If not, I just threw it away. I took the pairs of points, as well as the original map data, and transformed them to a gnomonic projection, where all great arcs are straight lines (thanks for finding the name of the projection, Graham!). Next, on the gnomonic plot, I connected the points I had found if the distance was over 2850 miles. It was pretty obvious that none of these were candidates since they all left the country.
I kept lowering the limit and eventually I finally found a line that was just barely tangent to the corner of the Florida Panhandle, as I had suspected.
One more note: for any gnomonic projection, we get to choose where
the projection plane is tangent to the sphere. If one chooses the
tangent plane to be tangent near the middle of the US, you get what
most maps look like. If you go off-center, you get crazier shapes,
but the key is that for ANY of the gnomonic plots, straight lines are
great arcs.
![]()
Return to Reality Carnival.
If you like stories like this, Reality Carnival has many more.