Grand
Internet Math Challenge
"The Grand Internet Math Challenge: Can you go beyond simple
magic squares?"
Copyright 1999, by Cliff Pickover
Please note: The wonderful results of this challenge are now published
in my book The Zen of Magics Squares, Circles, and
Stars (An Exhibition of Suprising Structures Across Dimensions) (Princeton
Unviversity Press, 2002). If you want to see how it all started, see below.
For this fun but difficult Internet math challenge, you
don't have to know more than the mathematics of addition. If you can find
an elegant solution to one of these, I'll try to put your solution in a
book and credit you so you will be forever remembered in the annals of
history. So very few of these have been solved.
(For all these problems, I prefer you use consecutive
numbers starting with 1, and that no numbers repeat, but if this is not
possible, you are free to relax the constraint. For example, start at a
number other than one.)
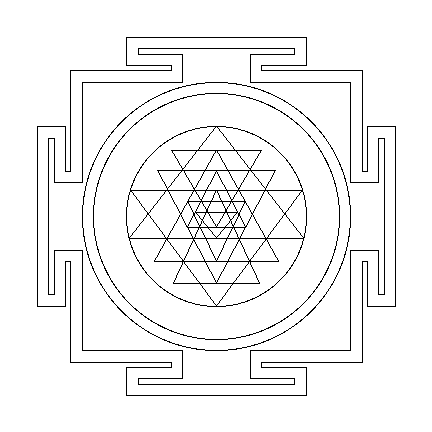
Mathematics and Mind: Yantra Magic Arrangements
Place an integer at each intersection point. If possible,
use integers that are consecutive. No integers should be repeated. The
sums of integers along each line (in the intersecting triangles and vertices)
or each circle (in the intersecting circle diagrams) should have the same
sum. Prize given to the first individual who solves each one of these.


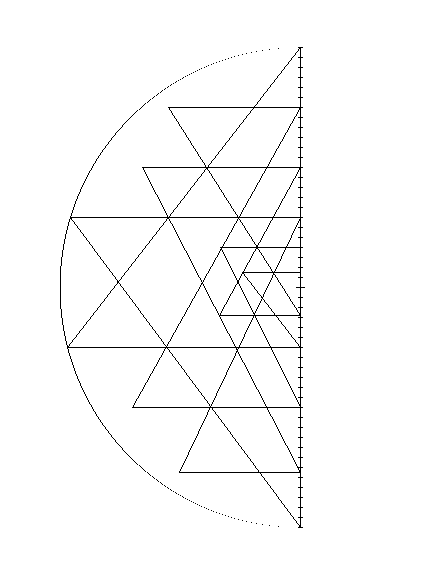
Seferovich
 Solution!
Solution!
Durga yantra image by Yantras
and Mandalas by PennyLea Mackie . Please visit this wonderful
site as soon as possible. You may purchase the exquisite fine art reproductions.
Nagle




Click on each image for magnification.
Can you place numbers on some of the vertices of these
incredible Nagle mandala images by Nagle
Design ? Please visit this wonderful site as soon as possible. You
may purchase the exquisite fine art reproductions.
Can you place numbers on these Rosicrucian symbols?
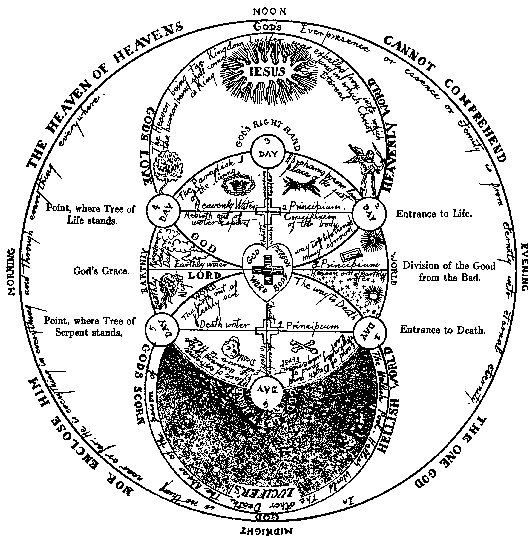

Can you place numbers on some of my own designs?
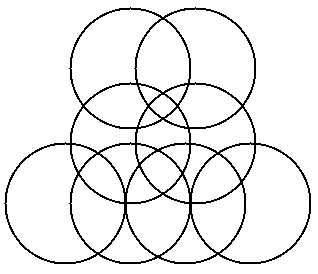
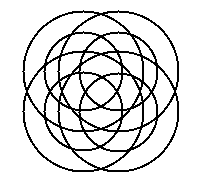
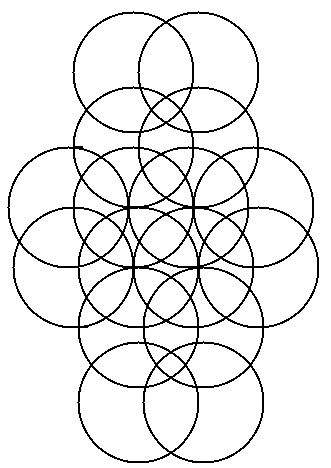
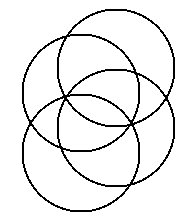 Solution!
Solution!
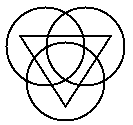 Solution!
Solution!
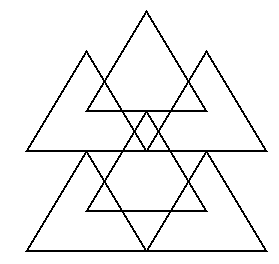
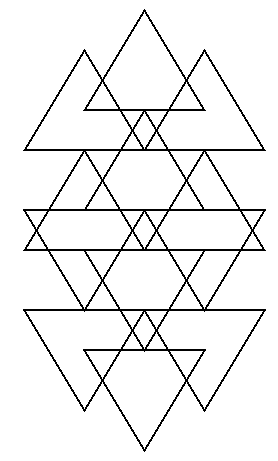
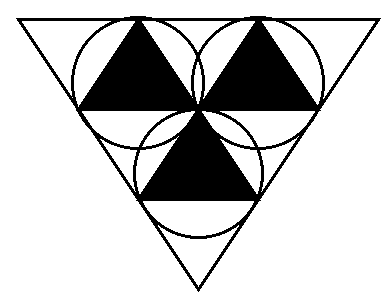 Solution!
Solution!
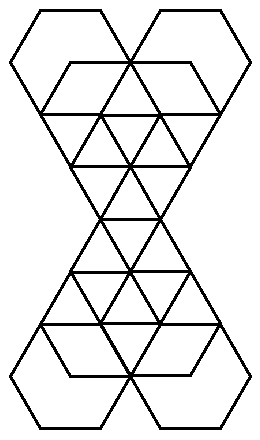

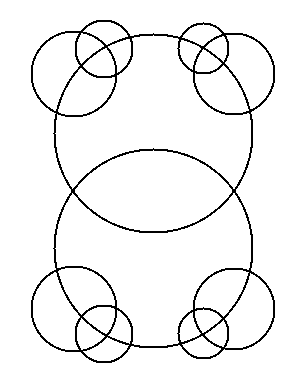 Solution!
Solution!
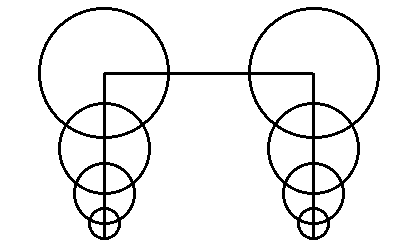 Solution!
Solution!
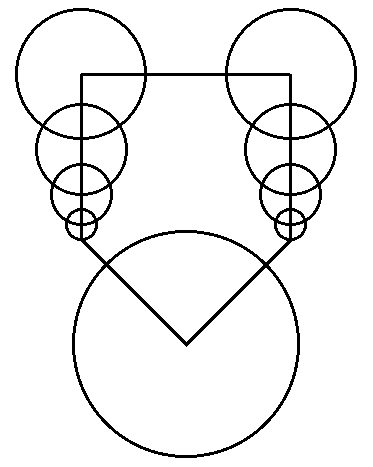
Rules: Place an integer in each cell so that when the
numbers in every row and column are added together, the sum is the same
constant.
Cube with cutout Tortured
cube Cube with cutout 2 Dissected
Cube Hyperdimensional frame cube CrossTwisted
world
Rules: 1) Look at the small squares. Place an integer
in each square. The sums of the integers forming a diagonal must always
be the same. Truncate the figure as you wish in order to remain sane.
2) Another set of rules for the same figure. You see two
kinds of cells. Cells A are small squares. Cells B are larger polygons
with a stairscase edge. Place an integer in each of the cells A so that
the sum of these integers adds up to the number in each Cell B. Be creative.
If you don't like these rules, make your own.
Hypercheckerboard
Each central star must contain an integer that is equal
to the sum of 6 numbers in each surrounding hexagon. Truncate the figure
as you wish in order to remain sane. (If you don't like these rules, make
up your own.)
Islam
Each petal has two spirals that intersect it. Place an
integer in each petal so that each spiral has the same sum.
Flower from Ganymede
Solution by the brilliant and
enigmatic Joseph DeVincentis. We do not currently know how many solutions
exist.
Place an integer at each of the vertices so that each diagonal sum
is the same. This sum must also be the same as the sum of the numbers along
the outer perimiter. What other interesting symmetries can you create?
A higher dimension
If these problems are too difficult, or do not seem elegant,
make up your own problem that has similar rules to those in magic squares
in which sums in various directions are the same. Send your figure to me,
and I'll try to publish it with your name.
Return to
Cliff Pickover's home page which includes computer art, educational
puzzles, fractals, virtual caverns, JAVA/VRML, alien creatures, black hole
artwork, and animations. Click here
for a complete list of over 20 Cliff Pickover books.



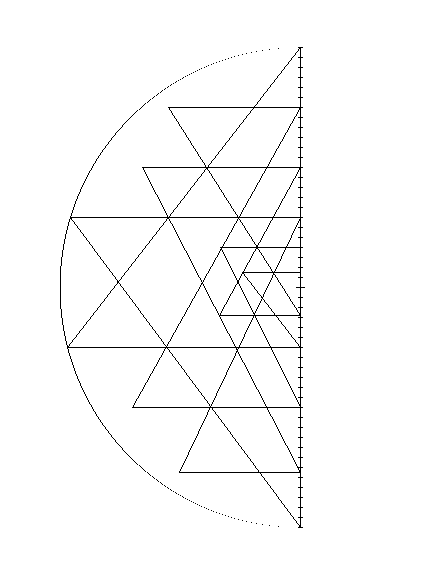



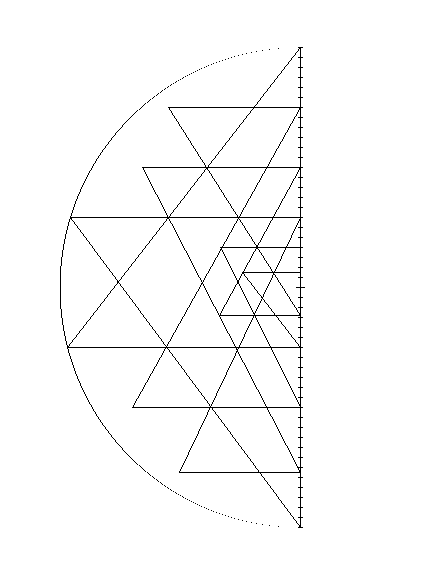
 Solution!
Solution!









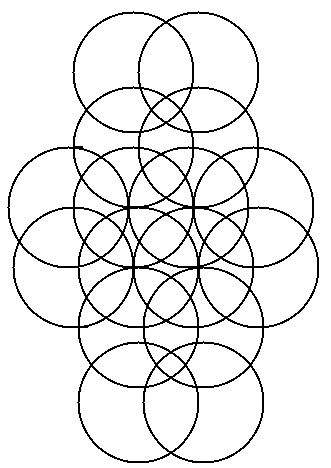
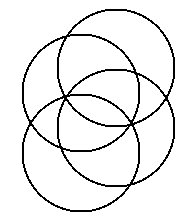 Solution!
Solution!
 Solution!
Solution!


 Solution!
Solution!