Multifractals
Chaos and Time-Series Analysis
11/28/00 Lecture #13 in Physics 505
 Comments on Homework
#11 (Nonlinear Prediction)
Comments on Homework
#11 (Nonlinear Prediction)
-
Results varied from almost too good to rather poor
-
Hard to diagnose the poor results when not enough detail given
-
You could try several data sets to see how general are your results
-
Here's sample results (averaged over 1000 realizations of the Hénon
map):
 Review (last
week) - Calculation of Fractal Dimension
Review (last
week) - Calculation of Fractal Dimension
-
Cover dimension
-
Find the number N of (hyper)cubes
of size d required to cover the object
-
D0 = -d log(N) / d log(d)
-
Capacity dimension
-
Similar to cover dimension but cubes are fixed in space
-
D0 = -d log(N) / d log(d)
-
This derivative should be taken in the limit d --> 0
-
Many data points are required to get a good result
The number required increases exponentially with D0
-
Examples of fractals
-
Some ways to produce fractals by computer:
-
Chaotic dynamical orbits (strange attractors)
-
Recursive programming
-
Iterated function systems (the chaos game)
-
Infinite mathematical sums (Weierstrass function, etc.)
-
Boundaries of basins of attraction
-
Escape-time plots (Mandelbrot, Julia sets, etc.)
-
Random walks (diffusion)
-
Diffusion limited aggregation
-
Cellular automata (game of life, etc.)
-
Percolation (fluid seeping through porous medium)
-
Self-organized criticality (avalanches in sand piles)
-
Similarity dimension
-
Example #1 (Sierpinski carpet):

D = log(8) / log(3) = 1.892789261...
-
Example #2 (Koch curve):
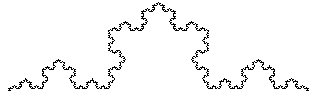
D = log(4) / log(3) = 1.261859507...
-
Example #3 (Triadic Cantor set):

D = log(2) / log(3) = 0.630929753
 Correlation Dimension
Correlation Dimension
-
Capacity dimension does not give accurate results for experimental
data
-
Similarity dimension is hard to apply to experimental data
-
The best method is the (two-point) correlation dimension (D2)
-
This method opened the floodgates for identifying chaos in experiments
-
Homework this week asked you to calculate D2 for
the Hénon map
-
Original (Grassberger and Procaccia) paper included with HW #12
-
Illustration for 1-D and 2-D data embedded
in 2-D
-
Procedure for calculating the correlation dimension:
-
Choose an appropriate embedding dimension DE
-
Choose a small value of r (say 0.001 x size of attractor)
-
Count the pairs of points C(r) with Dr
< r
-
Dr = [(Xi - Xj)2
+ (Xi-1 - Xj-1)2
+ ...]1/2
-
Note: this requires a double sum (i, j) ==> 106
calculations for 1000 data points
-
Actually, this double counts; can sum j from i+1 to N
-
In any case, don't include the point with i = j
-
Increase r by some factor (say 2)
-
Repeat count of pairs with Dr
< r
-
Graph log C(r) versus log r (can use any base)
-
Fit curve to a straight line
-
Slope of that line is D2
-
Think of C(r) as the probability that 2 random points
on the attractor are separated by < r
-
Correlation dimension emphasizes regions of space the orbit visits
-
Example: C(r)
versus r for Hénon map with N = 1000 and DE
= 2
-
Result: D2 = 1.223 ± 0.097
-
Compare: DGP = 1.21 ± 0.01 (Original
paper, N = 15,000)
-
See also my calculations (D2
= 1.220 ± 0.036) with N = 3 x 106
-
Compare: DKY = 1.2583 (from Lyapunov
exponents)
-
Compare: D0 = 1.26 (published result
for capacity dimension)
-
Generally D2 < DKY<D0
(but they are often close)
 Practical Considerations
Practical Considerations
-
Tips for speeding up the calculation (roughly in order
of increasing difficulty and decreasing value):
-
Avoid double counting by summing j from i+1 to N
-
Collect all the r values at once by binning the values of Dr
-
Avoid taking square roots by binning Dr2
and using log x2 = 2 log x
-
Avoid calculating log by using exponent of floating point variable
-
Collect data for all embeddings at once
-
Sort the data first so you can quit testing when Dr
exceeds r
-
Can also use other norms, but accuracy suffers
-
Discard a few temporally adjacent points if sample time is small for flows
-
Number of data points needed to get valid correlation dimension
-
Need a range of r values over which slope is constant
(scaling region)
-
Limited at large r by the size of the attractor (D2
= 0 for r > attractor size)
-
Limited at small r by statistics (need many points in each
bin)
-
Various criteria, all predict N increases exponentially with
D2
-
Tsonis criterion: N ~ 10 2 + 0.4D
(D to use is probably D2)
| D |
N |
| 1 |
250 |
| 2 |
630 |
| 3 |
1600 |
| 4 |
4000 |
| 5 |
10,000 |
| 6 |
25,000 |
| 7 |
63,000 |
| 8 |
158,000 |
| 9 |
400,000 |
| 10 |
1,000,000 |
-
Effect of round-off errors
-
Round-off errors discretize the state
space
-
Causes the measured dimension to approach zero at small r
-
This limits the useful scaling region of log C(r)
versus log r
-
Easy to test for this in low D since points will be identical
-
Effect of superimposed noise
-
Distinguishing chaos from noise
-
Chaos has dimension less than infinity
-
It may be unmeasurably high, however
-
White noise has infinite dimension
-
Colored (correlated) noise can appear low dimensional
-
Example: 1/f 2 (brown) noise
-
Conjecture: It's possible to get any C(r)
with appropriately colored noise
-
Start with an attractor of a dynamical system (or IFS)
-
Example: Triadic Cantor set (D = 0.631)

-
Visit the points on the attractor in random order
-
Geometry is accurately fractal, dynamics is random
-
Hence dimension can be low and well defined, but no chaos
-
This would presumably fail at sufficiently high embedding
-
A good demonstration of this would be a publishable student project
-
K-S entropy (Kolmogorov-Sinai)
-
Entropy is the sum of the positive Lyapunov exponents (Pesin
Identity)
-
A periodic orbit (zero LE) has 0 entropy (no spreading)
-
A random orbit (infinite LE) has infinity entropy (maximal disorder)
-
This is related to but different from the thermodynamic entropy
-
It is actually a rate of change of the usual entropy
-
Can be estimated from C(r, DE) in
different
embeddings
-
Formula: K = d log C(r)/dDE
in the limit of infinite DE
-
Hence, entropy can be obtained for free when calculating D2
-
Multivariate data
-
Suppose you have measured 2 (or more) simultaneous dynamical variables
(X and Y)
-
If they are independent, they reduce the required number of time
delays
-
Construct embedding from Xi, Yi,
Xi-1,
Yi-1,
etc...
-
Trick: Make single time series by intercalation
-
Xi, Yi, Xi+1,
Yi+1,
... and use existing D2 algorithm
-
Probably good to rescale variables to the same range
-
Get twice as much data this way in the same time
-
I'm not aware of this being discussed in literature but it
works
-
This could also be a publishable student project
-
Filtered data
-
What happens if you measure dX/dt or integral of X?
-
This has been examined theoretically and numerically
-
Differentiating is usually OK but enhances noise and lowers correlation
time
-
Integrating suppresses noise and increases correlation time - hard
to get a good plateau in C(r)
-
These operations can raise the dimension by 1 (adds an equation)
-
Other filtering methods have not been extensively studied (another
possible student project)
-
Missing data
-
What if some data points are missing or clearly in error?
-
Honest method:
-
Restart the time series
-
You lose DE - 1 points on each restart
-
Don't calculate across the gap
-
But you can combine the segments into one C(r)
-
Other options (if gap is of short duration):
-
Ignore the gap (probably a bad idea)
-
Set data to zero or to average (also a bad idea)
-
Interpolate or curve fit (OK if data is from a flow)
-
Use a nonlinear predictor to estimate the missing points (best idea)
-
None of these work if gap is of long duration
-
Nonuniformly sampled data
-
If sampling is deterministically nonuniform:
-
All is probably OK
-
Dimension may increase since additional equations come into play
-
If sampling is random:
-
This will give infinite dimension if randomness is white
-
If data is from a flow, and sample intervals are known, you can try to
construct
a data set with uniform intervals by interpolation or curve fitting
-
How accurate does sample time have to be? (good student
project)
-
Lack of stationarity
-
dx/dt = F(x, y)
-
dy/dt = G(x, y, t)
-
dz/dt = 1 (non-autonomous slowly growing term)
-
Increases system dimension by 1
-
Increases attractor dimension by < 1
-
If t is periodic, attractor projects onto a torus
-
Can try to detrend the data
-
This is problematic
-
How best to detrend? (polynomial fit, sine wave, etc.)
-
What is interesting dynamics and what is uninteresting trend?
-
Take log first differences: Yn = log(Xn)
- log(Xn-1) = log(Xn/Xn-1)
-
Surrogate data
-
Generate data with same power spectrum but no determinism
-
This is colored noise
-
Take Fourier transform, randomize phases, inverse Fourier
transform
-
Compare C(r), predictability, etc.
-
Many surrogate data sets allow you to specify confidence level
 Multifractals
Multifractals
-
Most attractors are not uniformly dense
-
Orbit visits some portions more often than others
-
Local fractal dimension may vary over the attractor
-
Capacity dimension (D0) weights all portions
equally
-
Correlation dimension (D2) emphasizes dense
regions
-
q = 0 and 2 are only two possible weightings
-
Let Cq(r) = S
[ S q(r
- Dr) / (N - 1)]q-1
/ N
-
Then Dq = [d log Cq(r)/d
log r] / (q - 1)
-
Note: for q = 2 this is just the correlation dimension
-
q = 0 is the capacity dimension
-
q = 1 is the information dimension
-
Other values of q don't have names (so far as I know)
-
q = infinity is dimension of densest part of attractor
-
q = -infinity is dimension of sparsest part of attractor
-
In general Dq < Dq-1
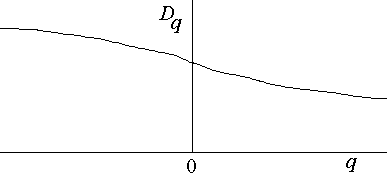
-
The K-S entropy can also be generalized
Kq = -log S piq
/ (q - 1)N
 Summary of Time-Series
Analysis
Summary of Time-Series
Analysis
-
Verify integrity of data
-
Graph X(t)
-
Correct bad or missing data
-
Establish stationarity
-
Observe trends in X(t)
-
Compare first and second half of data set
-
Detrend the data (if necessary)
-
Take first differences
-
Fit to low-order polynomial
-
Fit to superposition of sine waves
-
Examine data plots
-
Xi versus Xi-1
-
Phase space plots (dX/dt versus X)
-
Return maps (max X versus previous max X, etc.)
-
Poincaré sections
-
Determine correlation time or minimum of mutual information
-
Look for periodicities (if correlation time decays slowly)
-
Use FFT to get power spectrum
-
Use Maximum entropy method (MEM) to get dominant frequencies
-
Find optimal embedding
-
False nearest neighbors
-
Saturation in correlation dimension
-
Determine correlation dimension
-
Make sure log C(r) versus log r has scaling (linear)
region
-
Make sure result is insensitive to embedding
-
Make sure you have sufficient data points (Tsonis)
-
Determine largest Lyapunov exponent and entropy (if chaotic)
-
Determine growth of unpredictability
-
Try to remove noise (if dimension is too high)
-
Integrate data
-
Use nonlinear predictor
-
Use principal component analysis (PCA)
-
Construct model equations
-
Make short-term predictions
-
Compare with surrogate data sets
 Time-Series Analysis
Tutorial
(using CDA)
Time-Series Analysis
Tutorial
(using CDA)
-
Sine wave
-
Two incommensurate sine waves
-
Logistic map
-
Hénon map
-
Lorenz attractor
-
White noise
-
Mean daily temperatures
-
Standard & Poor's Index of 500 common stocks