Nonchaotic Multidimensional Flows

Comments on Homework #1 (The Logistic Equation)

• Some people didn't note sensitive dependence on conditions
• Please write a short summary of your results for each question
• Course grades are available on the WWW (check for accuracy)

Review (last week) - One Dimensional Maps (Logistic Map)

• X_n+1 = AX_n(1 - X_n)
• Control parameters and bifurcations
• Stable and unstable fixed points (attractors and repellors)
• Basin of attraction
• Periodic cycles (periodic attractors and repellors)
• Period-doubling route to chaos
• Bifurcation diagram (self-similar fractal)
• Feigenbaum numbers ("Feigenvalues")
• Chaos and periodic windows
• Stretching and folding (sensitive dependence)
• Transient chaos
• Eventually fixed points (preimages)
• Cantor set (infinite set of measure zero)
• Eventually periodic points
• Dense unstable periodic orbits
• Period-3 implies chaos (Li and Yorke)
• Numerical errors in logistic map calculation
• Probability density: P = 1 / p[X(1 - X)]^1/2
• Ergodic hypothesis
• Solution: X_n = (1 - cos(2ⁿcos^-1(1 - 2X₀)))/2
• Can be used to make fractal music

(see also The Music of José Oscar Marques)

Maps versus Flows

Maps:	Flows:
Discrete time	Continuous time
Variables change abruptly	Variables change smoothly
Described by algebraic equations	Described by differential equations
Complicated dynamics (in 1-D)	Simple dynamics (in 1-D)
Xn+1 = f(Xn)	dx/dt = f(x)
Example: Xn+1 = AXn	Example: dx/dt = ax
Solution: Xn = AnX0	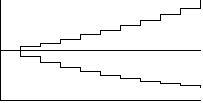Solution: x = x0eat
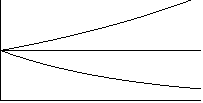Growth for A >1  Decay for A < 1	Growth for a > 0  Decay for a < 0
We call this an "orbit"	We call this a "trajectory"
n --> t,   A --> ea	t --> n,   a --> loge A

Logistic Differential Equation (1-D nonlinear flow)

• dx/dt = ax(1 - x)  [= f(x)]

f(x)
x
• Used by Verhulst to model population growth (1838)
• Equilibria (fixed points):  f(x) = 0 ==> x* = 0, 1
• Stable if df/dx < 0, unstable if df/dx > 0 (evaluated at x*)
• All initial conditions in (0, 1) attract to x* = 1 for all a > 0
• Oscillations and chaos are impossible
• Only point attractors (and repellors) are possible
• There can be many equilibria in nonlinear systems

Circular Motion (2-D linear flow)

• Ball on string, planetary motion, gyrating electron, etc.
• dx/dt = y,  dy/dt = -x, y₀ = 0
• Solution:  x = x₀ cos t  (or x₀ sin t)
• Note:  x² + y² = x₀² = constant (a circle of radius x₀)
• Equilibrium point at (0, 0) is called a center


• A center is neutrally stable (neither attracts nor repels)

Mass on a Spring (frictionless)

• Newton's second law:  F = ma  (a = dv/dt)
• Hooke's law (spring):  F = -kx
• Equation of motion:  mdv/dt = -kx
• This is a prototypical (linear) harmonic oscillator
• Let m = k = 1 (or define new variables)
• Then:  dv/dt = -x,  dx/dt = v
• Motion is a circle in phase space (x, v)
• 2 phase-space variables for each real variable
• This is because F = ma is a second order ODE
• Phase-space orbit is elliptical because energy is constant
• E = mv² / 2 + kx² / 2  ==>  x² + v² = constant  (for m = k = 1)
• There is no attractor for the motion (only a center)

Nonautonomous Equations

• These have t on the right-hand side
• Example: driven mass on a spring
• md²x/dt² = -kx + A sin wt
• Let m = k = 1 (for simplicity)
• dv/dt = -x + A sin wt
• dx/dt = v
• Let wt = f
• dx/dt = v
• dv/dt = -x + A sin f
• df/dt = w
• Can always eliminate t by adding a variable
• The f direction is periodic (period 2p)
• The motion is on a torus (a doughnut)

Damped Harmonic Oscillator

• Add friction to harmonic oscillator (i.e., F = -bdx/dt)
• dx/dt = v
• dv/dt = -x - bv
• Equilibrium:  x* = 0, v* = 0  (stable)
• Mechanical energy is not conserved (dissipation)
• Best undersood from phase portrait
• Types of equilibria for damped oscillator:

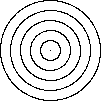
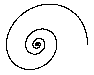
Spiral point (focus)  if b < 2 (underdamped)	Radial point (node)  if b > 2 (overdamped)

• Attractor --> sink,  repellor --> source
• Trajectory cannot intersect itself
• Poincare-Bendixson theorem (no chaos in 2-D)
• Chaos in flows requires at least 3 variables and a nonlinearity (next time)

Van der Pol Equation (2-D nonlinear ODE)

• Model for electrical oscillator, heart, Cephids
• dx/dt = y
• dy/dt = b(1 - x²)y - x
• Unstable equilibrium point (for b > 0):  x* = 0: y* = 0
• Growth for small x, y;  decay for large x, y
• Solution attracts to a stable limit cycle


• Basin of attraction is the whole x-y plane

Numerical Methods for solving ODEs

• dx/dt = f(x, y),  dy/dt = g(x, y)
• Let h be a small interval of time (delta t)
• This converts to flow to a map
• Euler method:
• x_n+1 = x_n + hf(x_n, y_n)
•  y_n+1 = y_n + hg(x_n, y_n)
• x and y are advanced simultaneously
• This is a first-order method
• It works poorly (orbit spirals out)
• Leap-frog method:
• Good if f = f(y) and g = g(x)
• x_n+2 = x_n + hf( y_n+1)
•  y_n+3 = y_n+1 + hg(x_n+2)
• x and y are advanced sequentially
• This is a second-order method
• Periodic orbit orbit closes exactly
• Can be modified for f(x_n, y_n) and g(x_n, y_n)
• Second order Runge-Kutta method:
• Trial step: k_x = hf(x_n, y_n), k_y = hg(x_n, y_n)
• x_n+1 = x_n + hf(x_n + k_x/2, y_n + k_y/2)
•  y_n+1 = y_n + hg(x_n + k_x/2, y_n + k_y/2)
• Can be extended to higher order (see HW #3)
• Fourth order is a good compromise