1
MOTION
 Motion, more properly called "mechanics," is the oldest branch of physics,
having been put on a firm quantitative basis by Isaac Newton (1642-1727)
who by the age of 24 had also developed calculus, which subsequently became
an indispensable tool of science. The study of motion is often viewed as
relatively mundane, but Albert Einstein (1879-1955) at the age of 26, while
employed at the Swiss Patent Office, thought deeply about the motion of
light and revolutionized our understanding of the relation of space and
time. The study of motion offers the opportunity to develop concepts such
as the conservation of energy that are relevant to all branches of physics.
With motion, these concepts are often exhibited in their least abstract
and most easily visualized form.
Motion, more properly called "mechanics," is the oldest branch of physics,
having been put on a firm quantitative basis by Isaac Newton (1642-1727)
who by the age of 24 had also developed calculus, which subsequently became
an indispensable tool of science. The study of motion is often viewed as
relatively mundane, but Albert Einstein (1879-1955) at the age of 26, while
employed at the Swiss Patent Office, thought deeply about the motion of
light and revolutionized our understanding of the relation of space and
time. The study of motion offers the opportunity to develop concepts such
as the conservation of energy that are relevant to all branches of physics.
With motion, these concepts are often exhibited in their least abstract
and most easily visualized form.
1.1
Bowling Ball Pendulum
A bowling ball suspended from the ceiling by a thin stainless steel wire
illustrates the simple harmonic oscillator and the conservation of energy.
MATERIALS
-
bowling ball: 16 pounds, 8.5-inch diameter
-
thin, stainless steel wire
-
footstool
-
stopwatch (optional)
-
softball (optional)
PROCEDURE
A volunteer, solicited from the audience, stands with the back of the head
against a wall with a bowling ball held snugly against the nose. The bowling
ball is released (not pushed!), and the instructor asks the volunteer to
put the hands by the side and not to move while the ball swings back to
within a few centimeters of the nose. It is best if the pendulum is as
long as possible, if the volunteer is far back from the point of suspension
and if the audience views from the side. A point on the wall should be
marked to indicate the proper position for the head, and a volunteer should
be chosen of approximately the correct height so that the head is in the
proper position, or a footstool should be provided. Glasses on the volunteer
add to the drama. Glassware or other fragile apparatus which happens to
be just millimeters below the trajectory of the ball heightens the interest.
With a stopwatch, or simply by counting the seconds, the time it takes
for the ball to swing out and back can be determined. The demonstration
can then be repeated with balls of different sizes and masses (a softball
works well) to show that the period, but not necessarily the frictional
losses, depend only on the length of the pendulum. The audience can be
asked to vote on whether a lighter ball will take a longer or a shorter
time to return to its starting point. By choosing different starting points
for the ball, or by observing the period carefully as the ball slowly comes
to rest, one can demonstrate that the period does not depend on the amplitude,
provided the amplitude is small. The demonstration can be used to emphasize
the deterministic nature of classical physics and the accuracy with which
certain (but not all) physical system systems can be predicted.
DISCUSSION
This demonstration illustrates the transformation of potential energy when
the ball is lifted above its resting position into kinetic energy as the
ball acquires velocity, and back, with energy losses due to friction with
the air. By measuring or estimating the amount by which the ball misses
the volunteer's nose, the fractional energy loss per cycle can be determined.
The period of the pendulum is given by 2pi(L/g)½, where
L is the length of the pendulum and g is the acceleration due to gravity
(9.8 m/s2). The period does not depend on the mass of the pendulum
or on the amplitude of the motion, at least so long as the amplitude is
sufficiently small. If the pendulum swings to an angle of 45° from
the vertical, the period is about 4% greater than calculated. At 90°,
the period is about 18% greater.
HAZARDS
The wire should have a tensile strength at least several times the weight
of the ball and should be anchored securely. Make very sure the ball cannot
strike anything during its swing, and stand in a position so that it can
be stopped if the volunteer gives it a push rather than just releases it.
1.2
Come-back Can
A can, when rolled across a table, comes to rest and then rolls back to
where it started, illustrating the concept of stored internal energy.
MATERIALS
-
cylindrical can with removable, opaque lid
-
rubber band
-
weight with hole though its center
PROCEDURE
A can is constructed with a rubber band strung between the center of its
ends and a weight connected to the band so as to cause the band to wind
up as the can rolls[1,2]. The can comes to rest and then rolls back to
where it started. The appearance is that the table is not level, but it
can be rolled in either direction with the same result. It helps to rotate
the can a turn or two before releasing it to compensate for the frictional
losses as it rolls. This also allows the can to roll up a slight incline.
One end of the can should be easily removable to reveal its contents and
to explain its operation.
DISCUSSION
This demonstration illustrates the conversion of kinetic to potential energy
and back. The potential energy is stored internally in the twisted rubber
band. On the microscopic level, the energy is stored in the electric potential
of the charged particles that make up the molecules of the rubber. Analogies
can be made to winding a watch, to filling an automobile gasoline tank,
to the stored energy in atoms and molecules and the energy of mass itself
(E = mc2).
From the standpoint of the special theory of relativity, the mass of
the can and its internal mechanism increases slightly as the rubber band
winds up, and it is this increased mass that is converted into kinetic
energy when the can begins to roll from a stop. One could estimate the
change in mass from (delta)mc2 = mv2/2 to show why
it is not normally detectable for objects moving slowly compared with the
speed of light. For example, if the can has an initial velocity of 1 m/s,
the fractional increase in its mass as it comes to rest amounts to less
than 1 part in 1017!
HAZARDS
There are no significant hazards with this demonstration.
REFERENCES
1. T. L. Liem, Invitations to Science Inquiry, Ginn Press: Lexington,
Massachusetts (1981).
2. J. P. VanCleave, Teaching the Fun of Physics, Prentice Hall
Press: New York (1985).
1.3
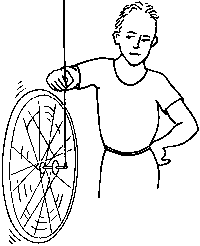
Bicycle Wheel Gyroscope
A bicycle wheel attached to a wire with a fishing line swivel and suspended
from a support makes an impressive gyroscope.
MATERIALS
-
bicycle wheel gyroscope*
-
stainless steel wire
-
fishing line swivel
-
rotating stool or platform* or swivel chair (optional)
-
suitcase with internal gyroscope (optional)
*Available from Carolina Biological Supply Company, Central
Scientific Company, Fisher Scientific, Frey Scientific Company and Sargent-Welch
Scientific Company
PROCEDURE
A bicycle wheel gyroscope is spun up to high speed by hand or with a rope
and is suspended from the ceiling by a wire with a fishing line swivel
attached to one end of its axle[1-3]. The fishing line swivel permits it
to precess. As the gyroscope precesses, its axis can be made to bob up
and down in a motion know as nutation. If a bicycle wheel gyroscope is
not available, the same effects can be seen on a smaller scale with a toy
gyroscope or even a toy top[4].
A strong volunteer from the audience can be asked to hold the spinning
bicycle wheel by one end of its axle horizontally at arms length and then
to raise it vertically over his head, first with the wheel not spinning
and then with it rotating rapidly. It is very difficult to do this without
a bit of practice. A spinning gyroscope mounted inside a suitcase provides
a particularly spectacular and unforgettable demonstration to the person
who tries to turn abruptly while carrying the suitcase.
The bicycle wheel can also be held in the hands while sitting on a rotating
stool or swivel chair or while standing on a rotating platform to illustrate
Newton's third law (action and reaction) and the conservation of angular
momentum. The stool can be made to rotate one direction or the other by
turning the axis of the bicycle wheel in different directions. The person
on the stool can hand the wheel to someone else who inverts it and hands
it back to the person on the stool who inverts it again, and so forth until
the stool is made to spin quite rapidly.
The gyroscope has many interesting properties. One can show that its
axis will remain horizontal so long as it is allowed to precess. When the
precession is stopped, it falls. The force required to make it move in
a particular direction must be applied at right angles to that direction.
When swung like a pendulum, the wheel tends to remain in a plane. This
is the principle of inertial guidance of rockets, the gyrocompass and other
navigational instruments[5]. One can point out that the gyroscopic action
of the wheels is one reason a bicycle remains upright[6,7]. In that case
there is no precession since the wheel is suspended from its center of
gravity. One can roll the bicycle wheel across the floor to illustrate
that it stays upright much longer than it would if released from rest.
A larger version of the gyroscope using a water-filled automobile tire
and other inexpensive parts easily obtained from junkyards can be built[8].
DISCUSSION
The gyroscope provides an interesting and unusual example of the conservation
of angular momentum. The angular momentum is a vector pointing along the
axis about which the gyroscope spins (in a sense given by the right-hand
rule). In the absence of external torques, the direction as well as the
magnitude of this vector will remain constant. Friction produces a torque
that decreases the magnitude of the vector and eventually causes the gyroscope
to stop spinning. Gravity produces a torque perpendicular to both the axis
of the gyroscope and the vertical, and thus causes the horizontal precession.
On a less abstract level, the precession can be explained in terms of the
downward pull of gravity that tries to make the wheel rotate faster at
the bottom than at the top. Since the wheel is rigid, this can happen only
if the wheel moves horizontally in the direction in which the bottom of
the wheel is spinning. The earth is a large gyroscope that precesses once
every 26,000 years due to the gravitational torque exerted by the sun on
the slight bulge at the equator.
Note that the precessional frequency is inversely proportional to the
frequency at which the gyroscope is spinning. This fact can be illustrated
by observing carefully the precession as the gyroscope slows down. Furthermore,
the precession frequency is independent of the angle that the axis makes
with the horizontal. The torque is greatest when the axis is horizontal,
but so also is the distance it has to move to precess once around, and
the effects just cancel.
The kinetic energy associated with the precession has to come from somewhere.
It comes from the gravitational potential energy of the gyroscope itself.
When the gyroscope is released from an initial fixed horizontal position,
it starts to fall in the usual manner. This falling motion rapidly transforms
into precession, with the center-of-mass
slightly lower than it was initially.
Actually, as it falls, it overshoots its equilibrium position slightly
and oscillates up and down about this equilibrium, resulting in nutation.
The nutation usually damps out rather quickly, but it can be excited by
a rapid upward or downward jerk on the free end of the axle of the gyroscope.
If there is friction acting to retard the precession, the center-of-mass
gradually falls until eventually the wheel hangs straight down.
HAZARDS
A spinning bicycle wheel is unwieldy and hard to control because of the
unique properties of the gyroscope. The rotation can be stopped by touching
the wheel against something (shirt not recommended!). Dizziness can be
induced very quickly by the rotating stool. If it doesn't make the subject
sick, it could cause the person to fall after getting off the stool. A
pause of a few moments to regain equilibrium before getting off is recommended.
REFERENCES
1. H. W. Dosso and R. H. Vidal, Am. Journ. Phys. 30, 528 (1962).
2. J. R. Prescott, Am. Journ. Phys. 31, 393 (1963).
3. C. T. Leondes, Scientific American 222, 80 (Mar 1970).
4. J. S. Miller, Physics Fun and Demonstrations, Central Scientific
Company: Chicago (1974).
5. H. F. Meiners, Physics Demonstration Experiments, Vol I, The
Ronald Press Company: New York (1970).
6. D. E. H. Jones, Physics Today 23, 34 (Apr 1970).
7. S. S. Wilson, Scientific American 228, 81 (Mar 1973).
8. H. A. Daw, Am. Journ. Phys. 56, 657 (1988).
1.4
Guinea and Feather Tube
In an evacuated glass tube, objects are observed to fall at the same rate
independent of their size, shape and mass.
MATERIALS
-
cylindrical glass tube with removable end and pumpout nozzle*
-
penny or other small dense object
-
feather or ball of cotton
-
vacuum pump
-
pressure gauge (optional)
-
heavy book and sheet of paper (optional)
*Available from Carolina Biological Supply Company, Central
Scientific Company, Frey Scientific Company and Sargent-Welch Scientific
Company
PROCEDURE
A glass tube at least a meter in length is equipped with a valve and nozzle
through which the tube can be evacuated with a mechanical vacuum pump.
Such a tube is called a guinea and feather tube because those were the
objects traditionally used when the demonstration was performed in England
centuries ago. The guinea was an English gold coin issued from 1663 to
1813 and valued at 21 shillings. These days, a modern coin and a feather
or ball of cotton are normally used.
The demonstration is introduced by asking the audience which falls faster,
a feather or a coin. (The question is reminiscent of the old joke about
which weighs more, a pound of feathers or a pound of lead.) Whichever answer
is given is either right or wrong depending upon whether the experiment
is performed in the air or in a vacuum. One can point out that in science
there are often opposing theories, and in such cases, experiments are required
to determine which theories are correct. Actually, an experiment usually
cannot prove that a theory is correct, only that it is incorrect.
One places the two objects in the tube at atmospheric pressure and rapidly
inverts the tube, yielding the expected result. The tube is then evacuated,
and the demonstration repeated. The two will fall at the same rate when
the tube is evacuated. Of course, the part of the demonstration not requiring
a vacuum can be done without use of the tube with the demonstrator standing
on the lecture table for a bit of extra drama.
If a vacuum pump is not available, an alternate form of the demonstration
can be done using a heavy book and a sheet of paper (smaller than the book)[1].
The two are first dropped side by side. The book will fall much faster.
The paper is then placed flat on top of the book and the two are released
together. They will fall at the same rate because the book eliminates the
air resistance that the paper would otherwise experience.
DISCUSSION
Legend has it that Galileo Galilei (1564-1642) performed this experiment
by dropping two cannon balls, one ten times heavier than the other, from
the Leaning Tower of Pisa[2]. The legend is almost certainly false, although
he was known to have performed similar experiments in his youth, always
getting the contrary result, which he attributed to the fact that the height
was not sufficient[3]. His arguments relied more on thought experiments
such as whether two identical objects connected together would fall at
the same rate as they would separately, rather then on actual experiments.
However, he did perform many experiments that upset Aristotelian physics
and paved the way for Newton in his development of the laws of motion[4,5].
On August 2, 1971, astronaut David Scott repeated the experiment with a
geologist's hammer and a falcon's feather while standing on the airless
surface of the moon while all the world watched on television.
The fact that a light object falls as fast as a heavy object in a vacuum
puzzles many people who correctly reason that gravity should pull harder
on the heavy object. However, from Newton's second law (F = ma), a harder
pull is required to accelerate a heavier object, and the effects just cancel.
This demonstration is an illustration of the equivalence of gravitational
and inertial mass and is the basis of the equivalence principle upon which
the general theory of relativity is based[6]. In 1890, the Hungarian physicist
Baron Lorand von Eötvös (1848-1919) refined Galileo's experiment
and showed that inertial and gravitational mass are the same to one part
in 108, and more recent experiments[7], motivated by the search
for a new form of force[8] have reached five parts in 1010.
For most objects, the resistance of the air noticeably alters the speed
with which they fall. For large objects moving at high speeds through air,
the drag force is given by Fd = C(rho)Av2/2, where
v is the speed, A is the cross-sectional area of the object measured in
a plane perpendicular to its motion, rho is the density of the air and
C is the drag coefficient. The drag coefficient is about 0.5 for spherical
objects but can be as high as 1 for irregularly shaped objects. By equating
the drag to the weight (Fd = mg), the terminal velocity is calculated
to be vt = [2mg/C(rho)A]½. The buoyant force
of the air contributes a small, additional, upward force on the object.
HAZARDS
A significant hazard of this demonstration is breakage of the glass tube,
especially if it strikes a hard object when it is rapidly inverted while
evacuated. Strong glass should be used, and great care should be exercised
during handling.
REFERENCES
1. T. L. Liem, Invitations to Science Inquiry, Ginn Press: Lexington,
Massachusetts (1981).
2. L. Cooper, Aristotle, Galileo and the Tower of Pisa, Cornell
University Press: Ithaca, New York (1935).
3. H. Butterfield, The Origins of Modern Science, Macmillan:
New York (1960).
4. A. R. Hall, From Galileo to Newton, 1630-1720, Harper and
Row: New York (1963).
5. S. Drake, Scientific American 228, 84 (May 1973).
6. D. Sciame, Scientific American 196, 99 (Feb 1957).
7. T. M. Niebauer, M. P. McHugh and J. E. Faller, Phys. Rev. Letters
59, 609 (1987).
8. E. Fischbach, D. Sudarsky, A. Szafer, C. Talmadge and S. H. Aronson,
Phys. Rev. Letters 56, 3 (1986).
1.5
The Monkey and the Coconut
A projectile directed at a stuffed monkey hits the monkey despite the fact
that the monkey begins to fall at the instant the projectile is fired.
MATERIALS
-
spring-loaded or pneumatic gun
-
stuffed monkey
-
electromagnet
-
microswitch or optical sensor
PROCEDURE
This popular demonstration usually goes by the name "The Monkey and the
Hunter," but is here modified to appeal to the sensitivity of those ethically
opposed to killing monkeys. The audience is asked to consider tossing a
coconut at a monkey who drops from a tree at the instant the coconut is
thrown and tries to catch the coconut. If the coconut is thrown directly
at the monkey in the tree, one might expect it to go above the monkey since
the monkey is falling. On the other hand, the coconut doesn't follow a
straight line. The audience is asked to vote on whether a coconut aimed
directly at the monkey will go above or below the monkey as he falls. Those
who abstain from voting are of course correct because the distance fallen
by the monkey and the coconut are precisely the same (neglecting air resistance)
during the time the coconut is in flight. This is best illustrated by drawing
a straight line to the position of the monkey in the tree. The coconut
falls below this line by the same distance the monkey drops in a given
time. The problem is slightly whimsical because the monkey is not likely
to react instantly to the release of the coconut, and air resistance acts
differently on the monkey and coconut.
The apparatus for this demonstration* usually consists of
some form of spring-loaded or pneumatic gun which can be electrically activated
and an electromagnet to support a stuffed monkey[1-4]. Alternately, the
gun can be fired mechanically and made to de-energize the magnet by a microswitch
or optical sensor. A useful embellishment is the ability to change the
vertical angle between the gun and the monkey and the ability to change
the speed of the projectile. Neither should have an effect on the outcome
of the demonstration. The effect is most dramatic if there is a considerable
separation between the gun and the monkey, but the allowable separation
is determined by the precision with which the apparatus is constructed.
It's best to hit the monkey every time even if one has to shorten the distance.
*Available from Fisher Scientific
DISCUSSION
This demonstration illustrates the fact that the vertical and horizontal
components are independent in projectile motion. The vertical acceleration
of an object is independent of both its horizontal and its vertical velocity.
Another common example of this idea is the problem of where to release
an object from a moving airplane in order to hit a target on the ground
and then to find where the airplane is in relation to the target when it
is hit.
Note that a collision will occur only if vosin(theta)o
> (gd/2)½, where vo is the initial speed of
the coconut, (theta)o is its initial angle with respect to the
horizontal, d is the initial elevation of the monkey above the ground and
g is the acceleration due to gravity (9.8 m/s2). If vosin(theta)o
is less than this value, the monkey cannot catch the coconut because the
coconut will strike the ground before reaching him. Also note that the
horizontal component of momentum must be conserved when the coconut strikes
the monkey, causing the monkey and coconut to continue moving in the direction
of the coconut but with a smaller velocity.
Those who have experience with guns will know that guns are "sighted
in" at a given distance (100 meters, for example) to account for the downward
displacement of the bullet during its travel. Thus when a fixed target
is closer than the distance for which the gun has been sighted, it is necessary
to aim below the target in order to hit it[5]. In such a case, with a falling
target, one would always have to aim below it.
HAZARDS
The danger in this demonstration is that the projectile will hit someone
in the audience either directly or after deflecting off something along
the path of its trajectory. Care should be taken in aiming the gun, and
objects that could deflect the projectile should be moved out of the way.
REFERENCES
1. B. F. Griffing and J. R. Priest, Am. Journ. Phys. 38, 1160 (1970).
2. A. A. Bartlett, H. Clark, R. Stoller, C. Zafiratos, G. Fladstol and
L. Laingor, Am. Journ. Phys. 43, 561 (1975).
3. B. Stahlberg and E. Personen, Am. Journ. Phys. 50, 470 (1982).
4. H. F. Meiners, Physics Demonstration Experiments, Vol I, The
Ronald Press Company: New York (1970).
5. R. A. Egler, Phys. Teach. 27, 356 (1989).
1.6
Ballistics Car
A car rolling across the table fires a projectile straight upward and subsequently
catches it, illustrating that the horizontal velocity of an object is independent
of the vertical force.
MATERIALS
-
car with spring-loaded mechanism*
-
steel ball*
-
cardboard or other tunnel (optional)
*Available from Carolina Biological Supply Company, Central
Scientific Company and Sargent-Welch Scientific Company
PROCEDURE
A small car which can be rolled across a table is equipped with a spring-loaded
mechanism that propels a steel ball vertically upward. As the car rolls
across the table, the string, which is attached securely to something on
the table, becomes taut and pulls out a pin releasing the spring without
significantly altering the velocity of the car. As it falls, the ball is
caught by the car.
The operation of the device is first explained to the audience, and
the pin is pulled out while the car is at rest. Finally, the car is rolled
across the table to complete the demonstration. As an embellishment, the
car can be made to go through a short tunnel while the ball goes over the
top of the tunnel. In a larger scale demonstration, a car large enough
for the lecturer to ride in can be used[1].
DISCUSSION
This demonstration illustrates the independence of the vertical and horizontal
motion of projectiles. Since the ball is launched from a car moving with
a constant horizontal velocity, the ball has the same horizontal velocity
as the car and thus remains directly above it (ignoring friction of the
wheels and the possibly different air resistance of the ball and the car).
Alternately, one can use this demonstration to illustrate the transformation
of coordinate systems. In the inertial system moving with the car, the
ball moves straight up and down. In the system fixed in the room, the ball
follows a parabolic trajectory.
HAZARDS
One should take care that the car does not roll off the edge of the table,
not so much because it might injure someone, but because the car could
be damaged if it fell on the floor. Also keep the area above the car clear
to prevent the ball from hitting anything.
REFERENCE
1. H. F. Meiners, Physics Demonstration Experiments, Vol I, The
Ronald Press Company: New York (1970).
1.7
Pail of Water
A pail of water can be swung around in a vertical circle without the water
spilling to illustrate Newton's first law of motion.
MATERIALS
-
pail of water with secure handle
-
bucket of confetti (optional)
-
tray with several water-filled wine glasses (optional)
PROCEDURE
The idea of centripetal and centrifugal forces and accelerations can be
dramatically illustrated with a pail partially filled with water. The pail
can be be swung around a vertical circle without the water spilling. One
can surreptitiously exchange buckets with one filled with confetti which
it then thrown into the audience. Other more precarious demonstrations
can also be done. The bucket can be replaced with a tray containing several
water-filled wine glasses. A rope attached to the tray through holes at
each of the four corners is used to swing the tray around in a circle[1].
A physics graduate student once volunteered his infant son in a basket
but changed his mind when his parental instincts (and perhaps the horror
of his wife) edged out his faith in the laws of physics!
DISCUSSION
According to Newton's first law of motion, objects in motion tend to remain
in motion unless acted upon by an external force. In this case, Newton's
law requires the water to continue moving along a tangent to the circle.
Thus a force is required to keep it always turning toward the center of
the circle. The interpretation of this demonstration is potentially confusing
when one considers that at the top of its arc, the water is accelerating
downward because of the motion, but that the force of gravity is also downward.
One can explain that F = ma is thus satisfied without the water leaving
the bucket. This demonstration provides the opportunity to discuss non-inertial
(accelerated) frames of reference and inertial (fictitious) forces (such
as the centrifugal force).
HAZARDS
The hazards of this demonstration are rather obvious. Make sure the area
is completely clear of obstructions and that the handle is securely attached
to the bucket. Also, don't swing the bucket too slowly!
REFERENCE
1. T. L. Liem, Invitations to Science Inquiry, Ginn Press: Lexington,
Massachusetts (1981).
1.8
Inertia Balls
The property of inertial mass is illustrated by pulling on a string attached
to the bottom of a heavy ball that is suspended by an identical string
until one of the strings breaks.
MATERIALS
-
heavy iron ball with hooks on opposite sides (2nd ball optional)*
-
several lengths of string
-
rigid support stand
-
rubber pad
*Available from Central Scientific Company, Fisher Scientific
and Sargent-Welch Scientific Company
PROCEDURE
Two identical heavy steel balls with hooks on opposite sides are suspended
from a support by strings[1]. It is important for the support to be quite
rigid. A string dangles from the bottom of each ball. The audience is told
that all the strings are identical and asked to vote on which string will
break first if the lower string is pulled on one of the balls. If the audience
votes that the upper string will break first, one reaches over and gives
the string a jerk in order to make it break below the ball. While the spectators
are puzzling over why their intuition was wrong, one offers to repeat the
experiment with the second ball while commenting on the importance of repeating
scientific experiments, but this time the string is pulled very gently
to make the string break above the ball. The audience is asked to explain
why the result was different. If the vote were the opposite, one would
reverse the order of the demonstrations. The importance of controlling
all the relevant variables in an experiment can be discussed. A single
ball can be used if one takes the time to retie the string between each
demonstration.
DISCUSSION
The explanation involves the inertia of the ball. With a quick jerk, the
ball has to accelerate, and a considerable force is required to do this
if the mass of the ball is large (F = ma). On the other hand, with a slow
pull, the acceleration is negligible, and the upper string is supporting
the weight of the ball plus the tension in the lower string, causing the
upper string to break. From Newton's second law, Tu - Tl
= m(g-a) where Tu is the tension in the upper string, Tl
is the tension in the lower string, m is the mass of the ball, g is the
acceleration due to gravity (9.8 m/s2) and a is the downward
acceleration of the ball. Thus the upper string breaks when the downward
acceleration of the ball is less than 9.8 m/s2; otherwise the
lower string breaks.
HAZARDS
The danger is that, when the upper string breaks, the ball falls on one's
hand or foot. The demonstration should be performed with a rubber pad underneath
to catch the ball, and the hand has to be removed quickly when the string
breaks.
REFERENCE
1. J. S. Miller, Physics Fun and Demonstrations, Central Scientific
Company: Chicago (1974).
1.9
Revolving Ball and Cut String
The requirement that an object move in a straight line in the absence of
an external force is illustrated by releasing a revolving ball at a certain
point in its orbit.
MATERIALS
-
styrofoam ball, brightly colored
-
motor with rotating arm
-
jack screw
-
razor blade or sharp knife
-
light string or thread
PROCEDURE
A styrofoam ball, preferably brightly colored, is attached to a light string
or thread and spun around in a circle at the end of an arm which is driven
by a motor. A sharp knife or razor blade is mounted on a jack screw so
that it can be slowly raised up to the point where it cuts the string.
When the string is cut, the ball flies off along a tangent to the circle.
The direction that the ball goes is controlled by the placement of the
knife.
DISCUSSION
This demonstration illustrates Newton's first law. When the string is cut,
there is no longer a radially inward force causing the ball to move in
a circle, and the ball continues along a straight-line trajectory except
for the effect of gravity.
The threat of cutting the string usually causes audience members to
cower in their seats since the ball looks heavy and dangerous and since
one intuitively believes that the direction the ball will go cannot be
accurately predicted. However, the ball will always fly off at right angles
to the line between the knife and the center of the circle. Thus one can
arrange its trajectory rather precisely. In any event, the ball is light
enough so as not to cause any injury.
HAZARDS
The main hazard is to the person doing the demonstration. The jackscrew
must be located close to the rotating arm, and thus one should take care
not to be hit by the rotating arm.
1.10
Toy Rockets
Newton's third law and the conservation of momentum are illustrated with
the use of toy rockets.
MATERIALS
-
toy rockets*
-
lawn sprinkler and compressed air (optional)
-
carbon dioxide fire extinguisher (optional)
*Available from Carolina Biological Supply Company, Central
Scientific Company, Fisher Scientific, Frey Scientific Company, Nasco and
Estes Industries (P.O. Box 227, Penrose, CO 81240)
PROCEDURE
Toy rockets are available from many toy stores as well as vendors of scientific
apparatus. Rockets suitable for indoor demonstrations use compressed air
and water[1] or a cartridge of compressed carbon dioxide as the propellant.
Solid propellant rockets are most safely demonstrated outdoors. More modest
demonstrations can be performed with balloons that rapidly expel their
air. With a water rocket, one can examine the effect of using different
proportions of air and water.
The rocket can be attached to a wire strung across the room or up to
the ceiling to control the direction that the rocket goes. The rocket can
also be placed on the end of a rotating arm to control its trajectory[1].
A lawn sprinkler run on compressed air provides an alternate demonstration
of the same principle as well as a demonstration of the conservation of
angular momentum. A crowd thinking the sprinkler is connected to water
rather than air quickly comes to attention when it is turned on!
A carbon dioxide fire extinguisher provides enough thrust for some impressive
rocket demonstrations. While sitting in a swivel chair or standing on a
rotating platform, one can be made to rotate very rapidly. A carbon dioxide
fire extinguisher mounted on a cart[2] or bicycle will propel one for several
hundred feet. Roller skates are another possibility.
DISCUSSION
The discussion is effectively introduced by contrasting the rocket with
all other vehicles which move by exerting a force on the medium across
which or through which they move. An automobile moves forward by virtue
of the reaction force between the wheels and the ground. An airplane moves
forward by the reaction force of the air which is pushed backwards by the
propeller or turbine blades. Many people misunderstand and think that a
rocket works by pushing against something. Throwing a basketball while
standing on a platform that is free to rotate helps to dispel this notion.
The rocket moves forward by the reaction force of the ejected exhaust
of the rocket itself. Stated differently, the total momentum of the rocket
and exhaust is constant. The general situation is described by the (nonrelativistic)
rocket equation vf = vi + veln(Mi/Mf),
where vi and vf are the initial and final velocities
of the rocket respectively, ve is the velocity of the exhaust
relative to the rocket and Mi and Mf are the initial
and final masses of the rocket respectively, considering the loss of mass
due to the ejected fuel. Alternately, one can explain the propulsion of
the rocket in terms of the center-of-mass of the rocket and exhaust moving
at a constant velocity. The thrust of the rocket is given by the magnitude
of the quantity vedM/dt and has the same units as force. The
thrust must exceed the weight (Mg) if the rocket is to get off the ground.
The kinetic energy of the rocket comes from the potential energy stored
in the form of a compressed gas (pressure times volume) or chemical bonds,
depending upon the type of propellant.
HAZARDS
Toy rockets can be very dangerous if aimed at someone. One should know
the characteristics of the rocket that will be used and practice firing
it in a direction that will not hurt anyone or damage nearby equipment.
REFERENCES
1. J. S. Miller, Physics Fun and Demonstrations, Central Scientific
Company: Chicago (1974).
2. F. Holt and G. Amann, Phys. Teach. 27, 560 (1989).
1.11
Rolling Chain
A rotating chain retains its round shape as it rolls across the lecture
table and objects in its path.
MATERIALS
-
small, flexible chain (about 60 cm long) wrapped into a loop
-
wooden disk to fit chain
-
electric motor
-
wooden stick
PROCEDURE
A chain wrapped around a wooden cylinder and spun up to a large rotational
velocity with an electric motor can be nudged off the cylinder with a stick[1,2].
The chain will retain its circular shape and will roll across the lecture
table and across objects in its path until eventually coming to rest in
a pile on the floor some distance away. The chain can be made to climb
a ramp and fly across the room. A 20-cm-diameter cylinder rotating at 2500
rpm makes an effective demonstration.
DISCUSSION
The chain retains its shape because of the inertia of each of its pieces
which tend to move in a straight line tangent to the circle. This tendency
is often ascribed to an outward centrifugal force, but it is not a force
at all. In fact the force is a centripetal force acting toward the center
of the circle in order to keep the chain from flying apart. Alternately,
one can describe the behavior of the chain in terms of the conservation
of angular momentum which requires it to continue rotating until sufficient
frictional torque brings it to rest.
HAZARDS
A reasonably light chain rotating at a modest velocity is relatively harmless
and can even be amusing if it tries to run over a person, but even so it
is best to aim it toward a wall and away from fragile equipment. It will
travel in a reasonably straight line unless deflected.
REFERENCES
1. H. A. Robinson, ed., Lecture Demonstrations in Physics, American
Institute of Physics: New York (1963).
2. J. S. Miller, Physics Fun and Demonstrations, Central Scientific
Company: Chicago (1974).
1.12
Moving Spool
A large wooden spool (or yo-yo) with a string wound around it from below
can be made to move either in the direction in which the string is pulled
or in the opposite direction depending upon the angle of the string with
respect to the horizontal.
MATERIALS
-
wooden spool or yo-yo
-
string
-
calipers and protractor (optional)
PROCEDURE
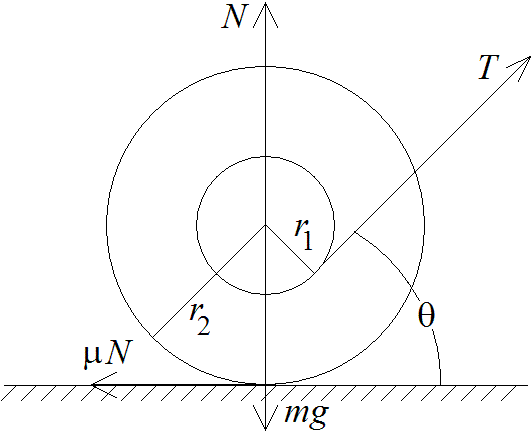 The demonstration[1]
is effectively introduced by asking the audience to predict whether the
spool will move forward or backward when the string is pulled. Whichever
way the majority of the audience votes, the spool can be made to go the
opposite direction by pulling the string at the appropriate angle. A small
angle (theta) between the string and the horizontal will make the spool
move in the direction of the pull, and a large (theta) will make the spool
move away from the pull. A change in angle so small that the audience does
not notice reverses the direction. The behavior of the spool is quite mysterious.
The demonstration[1]
is effectively introduced by asking the audience to predict whether the
spool will move forward or backward when the string is pulled. Whichever
way the majority of the audience votes, the spool can be made to go the
opposite direction by pulling the string at the appropriate angle. A small
angle (theta) between the string and the horizontal will make the spool
move in the direction of the pull, and a large (theta) will make the spool
move away from the pull. A change in angle so small that the audience does
not notice reverses the direction. The behavior of the spool is quite mysterious.
DISCUSSION
The explanation involves a consideration of the forces and torques on the
spool (see the diagram). It is easiest to consider the case where the string
is pulled with a force and at an angle such that the spool is just on the
verge of slipping without rolling. There are four forces: the weight (mg),
the upward normal force of the table (N), the tension in the string (T)
and the friction force (µN). If the spool is not yet moving, the
net horizontal force is zero, or T cos (theta) = µN. Only two of
the forces produce a torque about the center of the spool (T and µN),
and these torques must be equal and opposite if the spool is to slip rather
than rotate. Equating the torques gives r1T = r2µN.
Dividing this equation into the previous one gives cos (theta) = r1/r2.
Thus the critical angle that determines which way the spool will rotate
depends only of the ratio of the two radii and is independent of the mass
of the spool, the tension in the string and the coefficient of friction.
With calipers and a protractor, one can verify the predicted critical angle.
This is an especially interesting example of the equilibrium of a rigid
body.
HAZARDS
There are no significant hazards with this demonstration.
REFERENCE
1. J. S. Miller, Physics Fun and Demonstrations, Central Scientific
Company: Chicago (1974).
1.13

Stack of Cards
The static equilibrium of a rigid body is illustrated with a stack of cards
which have an impressive overhang.
MATERIALS
-
stack of cards, blocks or meter sticks
PROCEDURE
For a small audience, a deck of ordinary playing cards can be used. For
a larger group, a few dozen identical squares of cardboard or blocks of
wood provide better visibility. A more quantitative demonstration can be
done with a stack of meter sticks which could also be suspended in the
form of a mobile[1,2]. The uppermost card of the deck is slid horizontally
until it is just about to tip over (half of it must be supported by the
card underneath). The top two cards are then slid in the same direction
and so forth until the uppermost cards hang out a surprisingly large distance
beyond the base of the deck. For more drama, let the stack hang out over
the edge of the table[3]. The audience is then left to puzzle over why
the deck doesn't topple. A pair of card decks placed side by side and sheared
in opposite directions can be used to make an impressive, free-standing
arch.
DISCUSSION
The rule is that the stack of cards is in stable equilibrium as long as
the center of gravity of all the cards above a certain point lies over
a part of the card just underneath that point. The center of gravity of
the top card is at its middle, and so it can overhang by one half of its
width. When so placed, the center of gravity of the top two cards is such
that the second card can overhang by one fourth of its width. The third
card can overhang by one sixth of its width, the fourth by one eight and
so on (see the diagram). Thus the total overhang of the top card in a deck
of N cards is determined by the summation 1/2 + 1/4 + 1/6 + 1/8 + ···
+ 1/2N, which is a harmonic series with a sum equal to 0.5(0.5772 + lnN)
for large N. Thus one can get an arbitrarily large overhang by using a
sufficiently large number of cards. With 52 cards, the maximum stable overhang
is 2.27 times the width of a card. In the presence of surface tension,
which can be rather large if the cards have smooth surfaces, one can achieve
an even greater overhang than suggested by the above calculation.
HAZARDS
There are no significant hazards with this demonstration.
REFERENCES
1. R. Ehrlich, Phys. Teach. 23, 489 (1985).
2. I. MacInnes, Phys. Teach. 27, 42 (1989).
3. J. P. VanCleave, Teaching the Fun of Physics, Prentice Hall
Press: New York (1985).
1.14
Wilberforce Pendulum
A spring pendulum constructed such that the torsional and longitudinal
frequencies are nearly identical slowly transfers its energy back and forth
between the two modes of oscillation.
MATERIALS
-
spring pendulum with specially constructed mass*
*Available from Central Scientific Company
PROCEDURE
The phenomenon of resonance can be demonstrated with a simple but clever
device called a Wilberforce pendulum[1-6], named after Lionel Robert Wilberforce
(1861-1944), a demonstrator at the Cavendish Laboratory in Cambridge, England
around the turn of the century. It consists of a mass suspended from above
by a spring. Such a pendulum has three modes of oscillation: 1) the ordinary
swinging mode, 2) an oscillation along the axis of the spring and 3) a
torsional (twisting) mode. If the resonant frequencies of the second two
modes are nearly identical and one mode is initially excited, the other
mode will slowly acquire energy, and the energy will slowly transfer back
and forth between the modes.
DISCUSSION
The angular frequency of the swinging mode is given by (g/L)½,
where g = 9.8 m/s2 and L is the length of the pendulum. The
frequency of the spring oscillation is given by (k/m)½
where k is the spring constant and m is the mass supported by the spring.
Finally, the torsional frequency is given by (K/I)½ where
K is the torsional constant and I is the moment of inertia of the suspended
mass. Usually the moment of inertia is controlled by having several bolts
threaded into the mass in a symmetric arrangement. Nuts threaded on the
bolts can then be moved back and forth to change the moment of inertia
without altering the mass. Thus the two frequencies can be made nearly
equal.
If there were no coupling between the modes, the energy in each mode
would remain constant, ignoring friction, and the modes could be excited
in any combination with no subsequent interaction. In reality, the stretching
of the spring produces a small torque that excites the torsional mode.
The torsional mode, in turn, alternately stretches and compresses the spring,
exciting the spring mode. The necessity of having the frequencies nearly
equal is that the coupling between the modes is small, and thus the energy
must be transferred over a number of cycles. The effect is quite impressive
if the frequencies are carefully adjusted. This is an example of a harmonic
oscillator driven at its resonant frequency by a small driving force.
There are many other examples of coupled oscillators[7-16]. Usually
they consist of only two matched frequencies. A pair of adjacent pendula
(coupled pendula) attached together near the top with an elastic band or
weak spring is another common demonstration.
HAZARDS
There are no significant hazards with this demonstration.
REFERENCES
1. L. R. Wilberforce, Philos. Mag. 38, 386 (1894).
2. L. R. Wilberforce in Harmonic Vibrations and Vibration Figures,
edited by Herbert C. Newton, Newton and Company Scientific Instrument Makers:
London (1909).
3. V. Kopf, Am. J. Phys. 58, 833 (1990).
4. J. Williams and R. Keil, Phys. Teach. 21, 257 (1983).
5. R. J. Whitaker, Phys. Teach. 26, 37 (1988).
6. R. E. Berg and T. S. Marshall, Am. J. Phys. 59, 32 (1991).
7. H. A. Robinson, ed., Lecture Demonstrations in Physics, American
Institute of Physics: New York (1963).
8. M. G. Olsson, Am. Journ. Phys. 44, 1211 (1976).
9. T. E. Clayton, Am. Journ. Phys. 45, 723 (1977).
10. J. G. Lipham and V. Pollak, Am. Journ. Phys. 46, 110 (1978).
11. L. Falk, Am. Journ. Phys. 46, 1120 (1978).
12. L. Falk, Am. Journ. Phys. 47, 325 (1979).
13. M. G. Rusbridge, Am. Journ. Phys. 48, 146 (1980).
14. H. M. Lai, Am. Journ. Phys. 52, 219 (1984).
15. P. A. Bender, Am. Journ. Phys. 53, 1114 (1985).
16. H. F. Meiners, Physics Demonstration Experiments, Vol I,
The Ronald Press Company: New York (1970).
1.15
Reaction Time
The distance an object falls in the gravitational field of the earth can
be used as a sensitive measure of short time intervals.
MATERIALS
-
meter stick
-
crisp dollar bill
PROCEDURE
The usual demonstration consists of holding a meter stick vertically from
the top while a volunteer stands poised ready to catch it between the thumb
and forefinger[1]. If the fingers are opposite the 50-cm mark, for example,
when the meter stick is dropped, the position of the fingers when the meter
stick is caught gives a measure of the distance the meter stick fell before
the volunteer could react. The time is then calculated from d = gt2/2,
or t = (2d/g)½, where g = 9.8 m/s2 and d is
the distance dropped (in meters). For extra interest the demonstration
can be done using a crisp dollar bill with the volunteer's thumb and forefinger
opposite George Washington's portrait. The bill can be folded lengthwise
to ensure that it drops straight down undeflected by the air. Only a small
fraction of the volunteers are able to catch the bill. Without much risk,
one can offer the bill to the volunteer if it is caught.
Students can be encouraged to try this experiment at home, perhaps using
a yardstick and to compare their reaction time with that of their friends
and relatives. They can be asked to compare the reaction times of people
of different ages and to report back with the results.
DISCUSSION
In addition to illustrating the motion of an object under constant acceleration,
one can use such a demonstration to discuss the collection and analysis
of scientific data. By performing the experiment with a number of volunteers
and tabulating the results, one can explain the concepts of mean, average
and standard deviation. The results could be plotted as a histogram. The
fastest volunteers, in the tail of the distribution, can be told to go
race cars. Actually, reaction time is only one factor in the success of
a race car driver.
The time required for an object to fall provides a practical way to
measure, say, the depth of a well. Drop a rock into the well and measure
the time required for it to reach the bottom. The depth in feet is given
by 16t2 where t is the time in seconds. The height of a cliff
can be determined in similar fashion by throwing the rock horizontally
off the edge of the cliff.
HAZARDS
There are no hazards with this demonstration other than to the ego of the
slowest volunteers. Don't drop or throw rocks if there is any danger to
people or property below.
REFERENCE
1. H. F. Meiners, Physics Demonstration Experiments, Vol I, The
Ronald Press Company: New York (1970).
1.16
Beaker and Tablecloth
A glass beaker, partially filled with water, rests near the edge of a table
on a cloth which is rapidly pulled out from underneath the beaker without
spilling the water or breaking the beaker.
MATERIALS
-
large glass beaker with smooth bottom
-
smooth cloth without seam
PROCEDURE
The beaker is filled about two-thirds with water and placed on the cloth
some distance from the edge of the table. Make sure the cloth, table and
beaker are clean and completely dry. The table and the bottom of the beaker
should be smooth, and the cloth should not have a seam at the edge. Slowly
pull the cloth until the beaker is about 2 cm from the edge of the table
and then quickly jerk the cloth out from under the beaker. The beaker should
remain on the table, and no water should spill. As one gains confidence,
the demonstration can be done with other objects such as an entire table
setting, but it's easiest if the objects have smooth bottom surfaces. A
paper towel can be used instead of the cloth.
DISCUSSION
According to Newton's first law, an object at rest tends to remain at rest
until acted upon by an external force. In this case, the external force
is the friction force between the beaker and the moving cloth. The friction
force has a maximum value proportional to the mass of the beaker and its
contents, F = µmg, where µ is the coefficient of friction (typically
a few tenths) and g is the acceleration due to gravity (9.8 m/s2).
According to Newton's second law, this force produces a maximum acceleration
of a = F/m = µg. Thus if the cloth is pulled gently (acceleration
less than µg) the beaker accelerates along with it, but if the cloth
is jerked suddenly (acceleration greater than µg) the cloth is removed
before the beaker can accelerate to a significant velocity. What small
velocity it does acquire is quickly brought to zero by the friction between
the beaker and the table after the cloth has been removed. An additional
effect that contributes to the success of the demonstration is that the
coefficient of sliding friction is less than the coefficient of static
friction. Note that the mass of the object cancels, in contrast to popular
misconception[1], so that it is no easier to perform the trick with a heavy
object than with a light one. This fact can be illustrated by repeating
the demonstration with an empty beaker.
HAZARDS
This demonstration should be practiced to develop confidence that the beaker
will not break. It is important not to be timid about pulling the cloth.
Even so it is best to set up the demonstration in such a way that if the
beaker does break, there is no danger of injury. In particular, don't pull
the cloth toward the audience.
REFERENCE
1. T. L. Liem, Invitations to Science Inquiry, Ginn Press: Lexington,
Massachusetts (1981).
1.17
Inclined Plane
Objects sliding or rolling down an inclined plane are used to illustrate
friction and moment of inertia.
MATERIALS
-
straight, smooth board, at least a meter long
-
blocks of various materials
-
assorted cylinders, spheres and hoops
-
protractor (optional)
PROCEDURE
Blocks of various materials are placed on the plane (one at a time or simultaneously),
and the plane is tipped up to an angle at which the blocks just begin to
slide. One illustrates that the angle is different for different materials
such as smooth wood and rubber. Show that for a given material, the critical
angle is independent of the mass of the object and of the area of contact.
Show that the angle at which the block starts to slide is slightly greater
than the angle required to keep it sliding once it is in motion. The angle
can be measured with a protractor.
With the plane inclined at a fixed angle, one rolls cylinders, spheres
and hoops down the plane[1]. Before this is done, ask the audience to predict
which will reach the bottom first. Repeat with objects of different size
and the same mass and with objects of the same size and different mass.
Show that if the plane is inclined too steeply the objects will slide rather
than roll.
Compare the speed of an object rolling without slipping and one sliding
without friction (simulated by a large mass with small wheels). Both cases
approximately conserve mechanical energy, but the sliding object always
reaches the bottom before the rolling object because all the initial potential
energy is converted into translational energy with none wasted in rotation.
DISCUSSION
Friction exerts a force in the direction opposite to the direction in which
something is moving or trying to move. The friction force is proportional
to the normal force, which in this case is the component of the gravitational
force on the object in a direction perpendicular to the plane. If the plane
is inclined at an angle (theta) with respect to the horizontal such that
the object is sliding or just about to slide, the friction force is directed
upward along the plane and has a magnitude f = µW cos (theta), where
W is the weight and µ is the coefficient of friction. The quantity
µ is typically in the range of 0.01 to 1.0 and depends on the materials
and the condition (roughness) of the surfaces but not on the area of contact.
The coefficient of friction depends somewhat on the velocity of the object
and, in particular, is greater when the object is at rest (static friction)
than when it is in motion (kinetic friction).
The block will begin to slide when the component of the gravitational
force in a direction along the plane (W sin (theta)) just equals the friction
force, and thus tan (theta) = sin (theta) / cos (theta) = 1/µ, independent
of the weight W. A measurement of the critical angle (theta) at which the
block begins to slide thus provides a measure of the coefficient of friction.
Friction converts the potential energy of the block at the top of the incline
into heat as the block slides down so that it can arrive at the bottom
with no potential energy and very little kinetic energy.
When the angle of the plane is sufficiently small that an object can
roll down the plane without slipping, there is no relative velocity between
the point on the object that is in contact with the plane and the plane,
and thus the friction does no work on the object, and the total mechanical
energy is conserved. However, as the object rolls down the plane, its initial
potential energy is converted into both translational energy of the center-of-mass
and also into rotational energy. The ratio of the rotational to the translational
energy is I / mr2 where I is the moment of inertia, m is the
mass and r is the radius of the object. The moment of inertia is mr2
for a hoop, mr2/2 for a cylinder and 2mr2/5 for a
sphere. Thus the hoop acquires the most rotational energy and the least
translational energy (and velocity) and thus takes the longest to get down
the plane. The sphere is the fastest, and the cylinder is intermediate.
Since the initial potential energy and the final kinetic energy are both
proportional to mass and independent of the radius, objects of the same
shape but different mass and radius move down the plane at the same rate.
If the plane is inclined too steeply, the object will slip, friction will
do work, and the rate at which the objects roll is more difficult to predict.
HAZARDS
There are no hazards in this demonstration except to ensure that when the
objects reach the bottom of the incline, they are caught in a manner to
prevent them from doing any damage.
REFERENCE
1. J. S. Miller, Physics Fun and Demonstrations, Central Scientific
Company: Chicago (1974).
1.18
Coupled Pendula
Two rigid pendula with the same resonant frequency are connected near the
top with a rubber band, causing the energy to switch back and forth between
the two.
MATERIALS
-
two identical rigid pendula supported by a bar across the top
-
rubber bands or weak springs
PROCEDURE
With the rubber band removed, one shows that the two pendula are identical
with the same period and that they each swing independently of the other.
The rubber band or spring is attached between them, and both pendula are
brought to rest. One then starts one pendulum swinging in a plane perpendicular
to the rubber band. After a while, the first pendulum will stop swinging,
and the other will be swinging with a large amplitude. Then the first will
slowly begin swinging again while the second comes to rest and so forth
until the energy is damped away through friction. The demonstration can
be repeated with rubber bands or springs of different stiffness connected
at various distances from the pivot[1].
DISCUSSION
The rubber band provides a weak coupling between the two pendula allowing
the energy to slowly transfer from one to the other. The stronger the coupling
(stiffer rubber band, farther from the pivot), the more rapidly the energy
transfers. The phenomenon is the same as in the Wilberforce Pendulum.
The idea can be extended to any number of of pendula and serves as an
introduction to the motion of waves. In electrical circuits, energy is
often transferred from one resonant circuit to another tuned to the same
frequency by means of very weak electrical coupling. For radio and television
transmission, the transmitter and receiver must be tuned to the same frequency
and have narrow bandwidths.
HAZARDS
There are no significant hazards with this demonstration.
REFERENCE
1. J. S. Miller, Physics Fun and Demonstrations, Central Scientific
Company: Chicago (1974).
1.19
Random Walk
By repeatedly flipping a coin to determine the direction to turn, one can
execute a random walk.
MATERIALS
PROCEDURE
Ask the audience if anyone has ever been on a random walk (sometimes called
a "drunkard's walk"). Then offer to take them on one. Flip a coin. It it
comes up heads, turn to the right and take a big step. If it comes up tails,
turn to the left and take a big step. Repeat the process many times. Alternately,
illustrate the method with one or two steps and encourage people to go
out into a large field and try it themselves. Another method that takes
longer but works well when the streets in the neighborhood are lined up
in a regular rectangular pattern is to go a block between each flip of
the coin.
Since this demonstration takes some time and gets boring after a few
steps, it is ideal for a computer simulation. It is easy to program using
the random number generator available in most computer languages. For example,
a short program that will run under interpreted BASIC on most IBM-compatibles
is the following:
10 SCREEN 1
20 CLS
30 X=160
40 Y=100
50 A=INT(4*RND)
60 IF A=0 THEN X=X+1
70 IF A=1 THEN X=X-1
80 IF A=2 THEN Y=Y+1
90 IF A=3 THEN Y=Y-1
100 PSET(X,Y)
110 GOTO 50
The audience can be told that this pattern is what one would see from
an airplane flying high above someone who is executing a random walk. The
pattern produced is a fractal with dimension 1.5. It is halfway between
a line and a surface. The molecules in the air that we are breathing move
in a random walk except in a three-dimensional rather than a two-dimensional
space. They change direction when they collide with their neighbors, although
the change in direction is not always a right angle, and the distance they
go between collisions is not always the same.
DISCUSSION
Although the laws of classical physics are deterministic, where there are
many particles interacting with one another such as in a gas at atmospheric
density, the number of equations is very large, and it is a practical impossibility
to solve them all. In such cases, statistical methods are more appropriate,
and particles in such a collection will move in an effectively random manner.
If the particles behave like hard spheres, as they tend to do if they are
electrically neutral, they move in straight lines until a collision occurs,
whereupon the particles go off in arbitrary directions. Mechanical energy
is usually conserved in the collision, although energy may transfer from
one particle to the other. If the particles are electrically charged, the
forces are long-range, and the deviation from a straight line is gradual
and continuous, but the net result is the same. The same is true if the
particles are instead massive astronomical objects governed by long-range
gravitational forces.
A random walk is characterized by a distance d, called the mean free
path (the average distance a particle goes before it experiences a collision),
and a time (tau), called the collision time (the average time between successive
collisions). The ratio of the two is the speed of the particle, v = d/(tau).
The average distance a particle moves from its initial position after a
time t is given by r = d[t/(tau)]½ (the mean free path
times the square root of the number of collisions it has experienced).
The reason for the square root becomes clear if one considers a particle
that moves a distance d and then experiences a 90° collision and moves
another distance d. From the Pythagorean theorem, the particle has thus
moved a distance d(2)½ in a time t = 2(tau). Thus if
one flips a coin 100 times and takes a step in a random direction each
time, the average distance one goes is 10 steps. Don't expect this to work
after a single trial, but the average of a large number of trials should
approach the expected result.
HAZARDS
There are no significant hazards with this demonstration.
1.20
Chaotic Pendula
Various pendula can be made to exhibit chaotic motion when subjected to
a nonlinear restoring force.
MATERIALS
-
two disk-shaped magnets
-
steel ball on end of a string
-
tennis ball (optional)
-
overhead projector (optional)
PROCEDURE
A steel ball or other ferromagnetic object is suspended from a string so
that it comes within about two centimeters from a pair of disk-shaped magnets
about five centimeters apart[1]. The steel ball can be placed inside a
tennis ball to make the motion seem more mysterious. The whole apparatus
can be assembled on top of an overhead projector to improve visibility.
The pendulum when released exhibits chaotic motion. The motion eventually
stops with the ball over one of the magnets, but the trajectory depends
sensitively on the starting point.
This demonstration is best done after discussing and contrasting the
periodic motion of an ordinary pendulum. Point out that the difference
arises because the restoring force produced by the magnet is highly nonlinear
unlike the gravitational force whose tangential component is approximately
proportional to the angle the pendulum makes with the vertical. Each magnet
has associated with it a basin of attraction that determines which initial
conditions will approach that magnet. The basin boundary is a fractal.
DISCUSSION
Chaotic motion arises whenever a deterministic system exhibits behavior
that appears random and is sensitively dependent on the initial conditions.
It has only recently been widely understood that even very simple equations
can have such solutions. The equations, however, must involve a nonlinearity.
In this case, the nonlinearity arises from the attraction of the magnetic
dipole of the magnet to the induced magnetic dipole in the steel ball.
Such a force is very strong but of a very short range. With a single magnet,
the motion would always decay to a unique final state, called a "stable
fixed point." The second magnet allows two final states whose basins of
attraction meet at a fractal boundary. The boundary exhibits structure
no matter how greatly magnified. Thus two starting points near the boundary
can have completely different final conditions. This sensitivity to initial
conditions has been called "the butterfly effect," because the atmosphere
is presumably a chaotic, deterministic system, and thus a butterfly flapping
its wings in Brazil, say, can set off tornadoes in Texas. In fact, one
of the earliest examples chaos was discovered in a computer model of atmospheric
convection[2].
HAZARDS
There are no significant hazards with this demonstration.
REFERENCES
1. R. Ehrlich, Turning the World Inside Out, Princeton University
Press: Princeton, NJ (1990).
2. E. N. Lorenz, J. Atmos. Sci. 20, 130 (1963).
[Next Chapter] [Previous
Chapter] [Server Home]
J. C. Sprott
 Motion, more properly called "mechanics," is the oldest branch of physics,
having been put on a firm quantitative basis by Isaac Newton (1642-1727)
who by the age of 24 had also developed calculus, which subsequently became
an indispensable tool of science. The study of motion is often viewed as
relatively mundane, but Albert Einstein (1879-1955) at the age of 26, while
employed at the Swiss Patent Office, thought deeply about the motion of
light and revolutionized our understanding of the relation of space and
time. The study of motion offers the opportunity to develop concepts such
as the conservation of energy that are relevant to all branches of physics.
With motion, these concepts are often exhibited in their least abstract
and most easily visualized form.
Motion, more properly called "mechanics," is the oldest branch of physics,
having been put on a firm quantitative basis by Isaac Newton (1642-1727)
who by the age of 24 had also developed calculus, which subsequently became
an indispensable tool of science. The study of motion is often viewed as
relatively mundane, but Albert Einstein (1879-1955) at the age of 26, while
employed at the Swiss Patent Office, thought deeply about the motion of
light and revolutionized our understanding of the relation of space and
time. The study of motion offers the opportunity to develop concepts such
as the conservation of energy that are relevant to all branches of physics.
With motion, these concepts are often exhibited in their least abstract
and most easily visualized form.

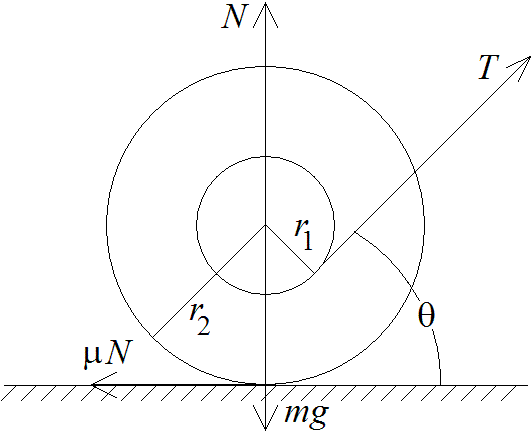 The demonstration[1]
is effectively introduced by asking the audience to predict whether the
spool will move forward or backward when the string is pulled. Whichever
way the majority of the audience votes, the spool can be made to go the
opposite direction by pulling the string at the appropriate angle. A small
angle (theta) between the string and the horizontal will make the spool
move in the direction of the pull, and a large (theta) will make the spool
move away from the pull. A change in angle so small that the audience does
not notice reverses the direction. The behavior of the spool is quite mysterious.
The demonstration[1]
is effectively introduced by asking the audience to predict whether the
spool will move forward or backward when the string is pulled. Whichever
way the majority of the audience votes, the spool can be made to go the
opposite direction by pulling the string at the appropriate angle. A small
angle (theta) between the string and the horizontal will make the spool
move in the direction of the pull, and a large (theta) will make the spool
move away from the pull. A change in angle so small that the audience does
not notice reverses the direction. The behavior of the spool is quite mysterious.
