In the MST device, a magnetized plasma is confined by a magnetic field in a configuration called a reversed field pinch (RFP).  The plasma exhibits magnetic and other fluctuations that are believed to be responsible for the rapid escape of the plasma across the magnetic field to the walls where it is cooled.  This anomolous transport is a major impediment to the development of magnetic fusion energy.  Since the dynamics producing the fluctuations are deterministic, the fluctuations are presumably chaotic with a high dimension.  In fact, Watts placed a lower limit of about 15 on the correlation dimension of the observed magnetic turbulence in MST.  If chaotic fluctuations are responsible for the anomolous transport, it would be of great benefit to control their characteristics.  On way this might be done is to apply a sinusoidal perturbation of some carefully chosen frequency to some accessible system parameter.  In the most optimistic case, this perturbation would suppress the chaos and reduce the dynamics to a simple limit cycle with a concurrent substantial reduction in plasma transport.

On way to study such prospects is to construct an artificial neural network model of the magnetic dynamics of MST and to add periodic perturbations to the model in a numerical simulation.  The neural net chosen has N neurons, with the input of each neuron consisting of the superposition of the weighted sum of the output of all the neurons (including itself).  The neurons are represented by hyperbolic tangent squashing functions that provide the nonlinearity necessary for chaos:

The parameter s is a scale factor on the weights and is initially chosen as s = 1.  The N x N matrix of weights W_ij is adjusted by a variant of simulated annealing so that the N outputs of the neurons X_i(t+1) at T successive time steps fits an N x T matrix of training points obtained from an array of N magnetic pickup coils spaced uniformly around the torus wall and measuring the time derivative of the poloidal magnetic field (dB_p/dt).  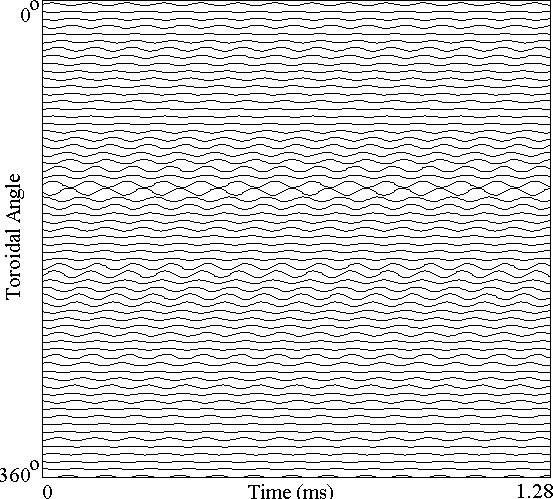The training set used has N = 64 and T = 255, with a sample time of 5 ms (200 kHz sample rate) and was rescaled so that the data fall in the range -1 to +1 as shown below:

In the data, the dominant feature is a rotating resistive tearing mode with a frequency of about 14 kHz.

After training the net for several days of 200 MHz CPU time, the output of the network on the same scale as above has the waveform shown below:

The simulation does capture some sense of the rotating mode seen in the experiment, with a frequency of about 11 kHz.  It appears that the signal from the 26th coil from the top might be accidentally inverted, and this blemish is captured by the neural net.  The model is not chaotic, however, as evidenced by calculation of the largest Lyapunov exponent, which is indistinguishable from zero, and the solution appears to be a limit cycle in this 64-dimensional space.  To obtain a chaotic solution, the parameter s was increased to 1.2, giving the result below:

This case has a largest Lyapunov exponent (base-e) of 0.028/iteration.  The rotating oscillation persists at a frequency of about 10 kHz.

To this case was added a perturbation s = s₀ + s₁ sin (2pft)] with s₀ = 1.2, and the perturbation amplitude was scanned over the range 0 < s₁ < s₀ and frequency over the range 1 kHz < f < 100 kHz, and the largest Lyapunov exponent was calculated for each combination of s₁ and f.  The result was plotted with a gray scale in which the darkest color (black) indicates an exponent of zero (chaos completely suppressed) and the lightest color (white)  indicates an enhancement of the chaos (doubling of the Lyapunov exponent):

The general result is a decrease in chaos for increasing perturbation amplitude, with certain frequencies such as 13 kHz being especially effective.  The striations in the upper left are caused by truncating the calculation at a time (500 iterations) that is not an integer number of perturbation cycles.  Since the Lyapunov exponent generally increases with s, chaos is enhanced when the final value of s is positive and diminished when it is negative.