Misiurewicz Point of the Logistic Map

J. C. Sprott

Department of Physics, University of Wisconsin, Madison, WI 53706, USA
April 28, 2005
(revised May 8, 2006)

In the logistic map

Xn+1 = AXn(1 - Xn)

the (first) Misiurewicz point is the combination of (A, X) for which an initial condition at the critical point X0 = 0.5 (the value at which the first derivative is zero) converges to X after three iterations and thereafter remains there. It marks the point at which two chaotic bands coalescence into one, and it is the point at which the measure (probability density) is maximum as shown below:

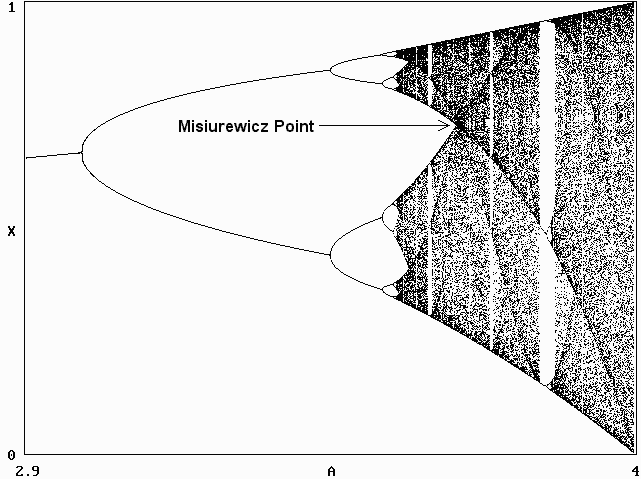
Bifurcation diagram

The exact value was determined by zooming into the corresponding region of the (A, X) diagram by a factor on the order of 1015 with nine iterations starting with an initial condition of X0 = 0.5, and the result is shown below:

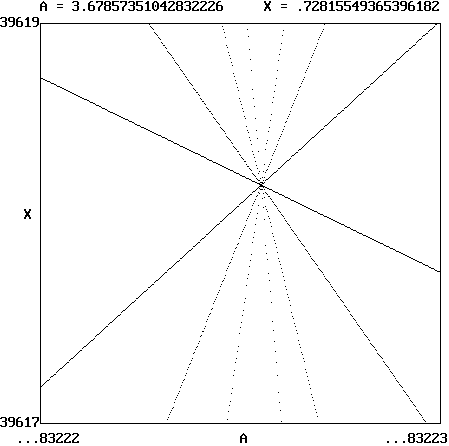
Misiurewicz Point

The calculated Misiurewicz point is A = 3.67857351042832226... at X = 0.728155493653961819...

According to Daniel Stoffer of the Mathematics Department at ETH-Zurich, A satisfies the equation A3 - 2A2 - 4A - 8 = 0, and X follows from X = 1 - 1/A. He also points out that the Misiurewicz point has the following properties:
  1. For any A less than or equal to the Misiurewicz point, the logistic map admits no periodic point of odd period except for a fixed point. For any A greater than the Misiurewicz point, the logistic map admits periodic points of odd period > 1. For A > 3.628 but less than or equal to the Misiurewicz point, the logistic map admits periodic points of any even period.
  2. If A is less than or equal to the Misiurewicz point, then the logistic map does not admit a snap-back repellor. (For the notion of a snap-back repellor, see F. Marotto, Snap-back repellors imply chaos in Rn, J. Math. Anal. Appl. (1978).)
Ref: M. Misiurewicz, Absolutely continuous measures for certain maps of an interval, Publ. Math. I.H.E.S. 53, 17-51 (1981).


Back to Sprott's Technical Notes