Horton and Doxas (J. Geophys. Res. 103, 4561 (1998)) proposed a dynamical model of the Earth's magnetosphere (WINDMI model) which can be reduced to a set of six first-order ordinary differential equations whose solutions are chaotic under some conditions. Smith, Thiffeault, and Horton (J. Geophys. Res., in press) expressed these equations in dimensionless form as
dI/dt = a1(Vsw - V) + a2(V
- Vi)
dV/dt = b1(I - I1) - b2P1/2
- b3V
dP/dt = V2 - K||1/2P{1
+ tanh[d1(I - 1)]}/2
dK||/dt = P1/2V - K||
dI1/dt = a2(Vsw
- V) + f1(V - Vi)
dVi/dt = g1I1
- g2Vi - g3I11/2Vi3/2
and gave values for the parameters for which various dynamical behaviors occur. In particular, chaos was observed for:
Vi = V + a2(Vsw
- V)/f1
I1 = g32Vi3/2g12
+ g2Vi/g1 + (g3Vi2/2g12)(4g1g2
+ g32Vi2)1/2
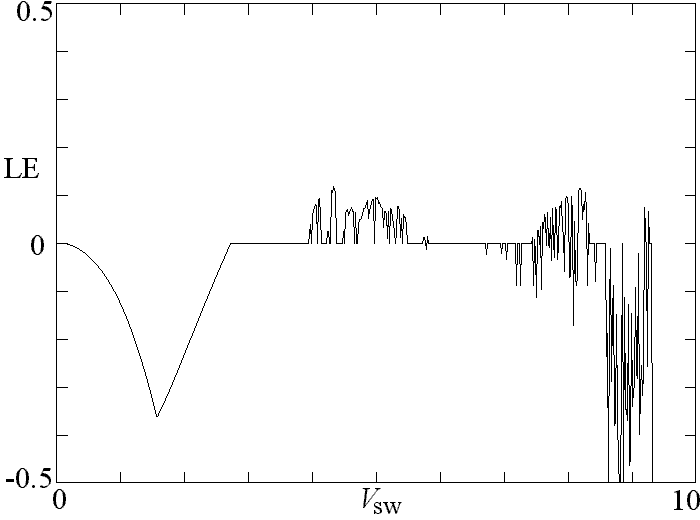
This reduced 4-dimension system was solved numerically, and the results are very similar to the full 6-dimensional case. In particular, the plot below shows the largest Lyapunov exponent (base-e) as Vsw is varied from 0 to 10.

Negative values imply stable fixed point solutions, zero values imply limit cycles or perhaps toruses, and positive values imply chaos. The attractors in the various regions resemble those for the full 6-D system. In the chaotic region, the Lyapunov exponent is typically about 0.1, implying a growth time of errors in the initial conditions of about 3 hours, and the correlation dimension is close to 2.0. The calculation that produced the above plot is available as PowerBASIC source code and DOS executable object code. It uses a fourth-order Runge-Kutta integrator with a step size of 0.1 and 200,000 iterations for each Vsw value.
It turns out that a2, g2, and g3 can all be set to zero simultaneously without destroying the chaos and gives a plot very similar to the above. Furthermore, the fourth equation can apparently be eliminated as well, giving K|| = P1/2V, for which chaos still occurs. Finally, the V in the third equation can be replaced with its equilibrium value of Vsw. Putting in all these simplifications gives the following 3-D system:
dI/dt = a1(Vsw
- V)
dV/dt = b1I - b2P1/2
- b3V
dP/dt = Vsw2 - P5/4Vsw1/2{1
+ tanh[d1(I - 1)]}/2
A further simplification results from replacing P in the third equation with its equilibrium value, P = (b1/b2 - b3Vsw/b2)2. Now define new variables,
x = d1(I
- 1)
y = a1d1(V - Vsw)
z = a1b2d1P1/2
+ a1d1(b3Vsw
- b1)
in terms of which the 3-D system above can be written as
dx/dt = -y
dy/dt = c1x - b3y - z
dz/dt = -c2 - c3tanh(x)
where c1 = a1b1, c2 = a1d1(b1 - b3Vsw)3/2(Vsw/b2)1/2/4 - a1b22d1Vsw2/2(b1 - b3Vsw), and c3 = a1d1(b1 - b3Vsw)3/2(Vsw/b2)1/2/4. The system has thus been reduced to one with 6 terms, 4 parameters, and a single nonlinearity. As a check of the algebra and to verify that the approximations are reasonable, the largest Lyapunov exponent for this system is plotted versus Vsw below:

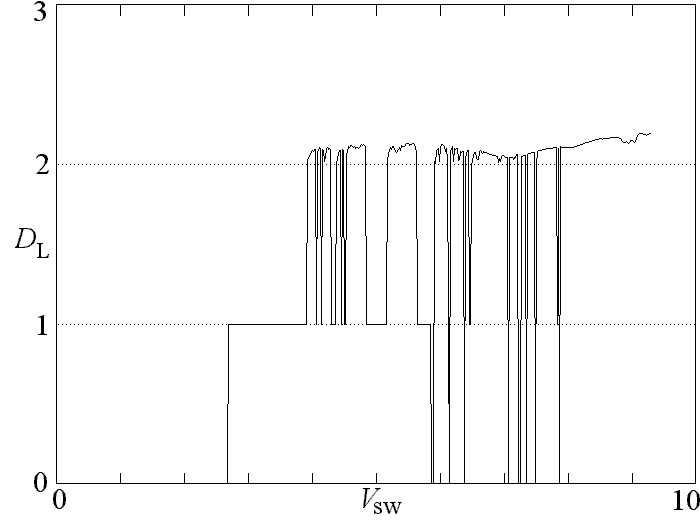
The agreement is reasonably good. The Lyapunov (or Kaplan-Yorke) dimension can be calculated from the spectrum of Lyapunov exponents. Its value versus Vsw as plotted below resembles the plot of the largest Lyapunov exponent above:
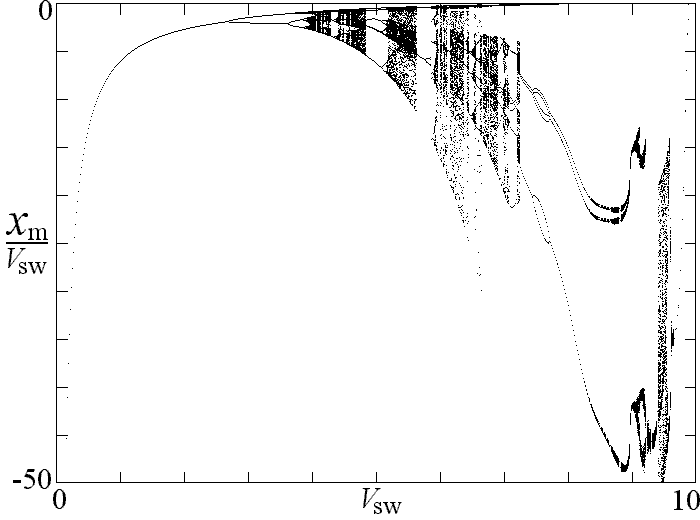
The regions of various dynamical behaviors can also be exhibited in a bifurcation diagram in which the local minima or maxima of x are plotted versus Vsw. Such a plot as shown below clearly indicates the regions of periodicity and chaos:
An audio file (WAV format) allows you to listen to the sound produced by the x variable as Vsw is slowly varied from about 3 to 10. The attractor for Vsw = 4.8 as shown below looks almost identical to Figure 12 of Smith, et. al.

The value of Vsw used by Smith, et. al. lies in a periodic of the reduced 3-D system. There should be little doubt that the hyperbolic tangent is the important nonlinearity in producing the chaos. The 3-D system has a fixed point at x* = -tanh-1(c2/c3), y* = 0, z* = c1x* with eigenvalues L that satisfy
L3 + b3L2 + c1L + c3 - c22/c3 = 0
A Hopf bifurcation occurs at c1b3 = c3 - c22/c3 followed by a period doubling route to chaos.
For this system, the sum of the Lyapunov exponents is -b3. From the calculated value for the largest exponent and the fact that one exponent must be zero, the entire spectrum can be obtained for the above parameters as (0.145, 0, -1.205). The Lyapunov (or Kaplan-Yorke) dimension is 2 + 0.145/1.205 = 2.12 in excellent agreement with the calculated correlation dimension of 2.14.
The simplification can be carried one step further by reducing the system to a jerk form (a third-order explicit ODE with a scalar variable):
x''' + b3x'' + c1x' = -c2 - c3tanh(x)
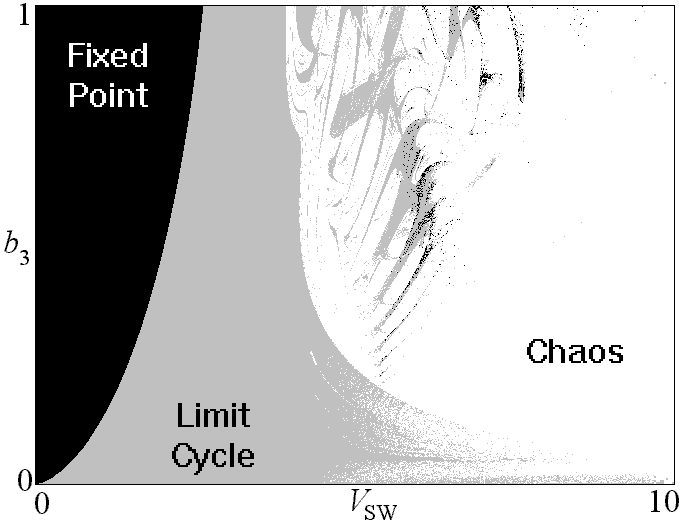
where x' = dx/dt, etc. This is a special case of a damped harmonic oscillator driven by a nonlinear memory term, whose solutions have been studied and are known to be chaotic. See, for example, J. C. Sprott, Phys. Lett. A. 266, 19-23 (2000) and J. C. Sprott, Am. J. Phys. 68, 758-763 (2000). The period of the dominant frequency of oscillation is 2pi/c11/2 = 3.85, corresponding to a real time of about 1 hour. In the equation above, t can be rescaled by c11/2 to eliminate one of the four coefficients. The dynamical behavior is thus determined by only three parameters. The regions of various dynamical behaviors are plotted in the b3-VSW plane below with the other parameters as listed above:
This system could be implemented electronically since a saturating operational amplifier produces a good approximation to the tanh(x) function, although the behavior is somewhat sensitive to the exact nature of the nonlinearity. A circuit for doing this is shown below:
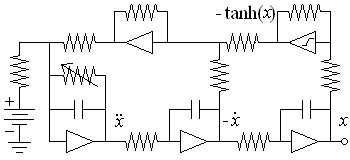
All the operational amplifiers are linear with only their inverting inputs shown except for the one in the upper right, which is designed to saturate when the input voltage x exceeds one volt. The noninverting input of each amplifier is grounded. The variable resistor corresponds to 1/b3 and can be used as a bifurcation parameter. The frequency can be scaled so that the circuit operates in the audio range for easy study and demonstration.
The system above is equivalent to
x''' + bx'' + x' = -c2 - c3 tanh(x)
with b = 0.65, c2 = 3413.8, and c3 = 3415.1. This suggests defining e = c3 - b << b and writing the system as
x''' + bx'' + x' = e - c[1 + tanh(x)]
Then optimal values of the parameters b, c, and e were sought that maximized the largest Lyapunov exponent using a variant of simulated annealing with the result b = 0.7, c = 70, and e = 1.15, giving a Lyapunov exponent of ~0.11. The result is not very sensitive to c in the limit of large c. Thus it appears the case above is close to the optimum, and we are free to choose c according to some physics criterion. Furthermore, the Lyapunov exponent is only slightly reduced (LE ~ 0.07) by setting e = 1, which makes the system a bit more elegant, and reduces it to a 2-parameter system for which the following graph shows the regions of chaos in bc space:
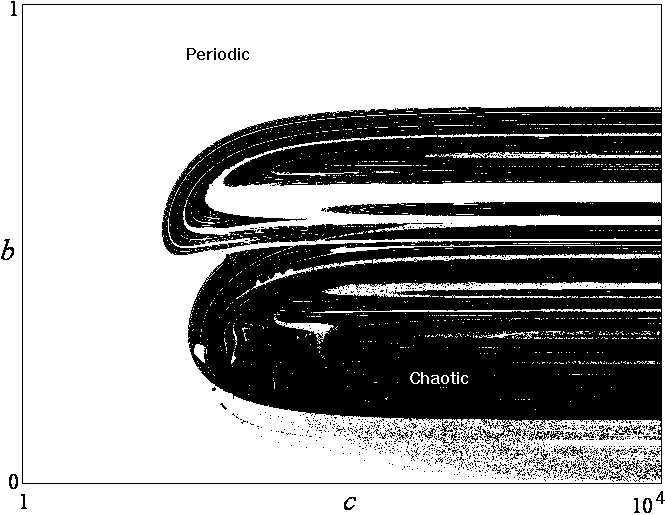
There are no bounded solutions for e = 0, since the righthand
side is then negative definite.
Replacing the 1 + tanh(x) term with a Heaviside function gives
solutions that are only weakly chaotic, if at all. Thus the results
are sensitive to the shape of the step.
This system has an equilibrium point at x* = tanh-1(e/c - 1), y* = 0, and z* = 0, which undergoes a Hopf bifurcation at b = 2e to a limit cycle that increases in size until chaos onsets. Defining a as the average distance of the trajectory from the equilibrium point, numerical calculation gives the following graph of a versus b for e = 1 and c = 70:
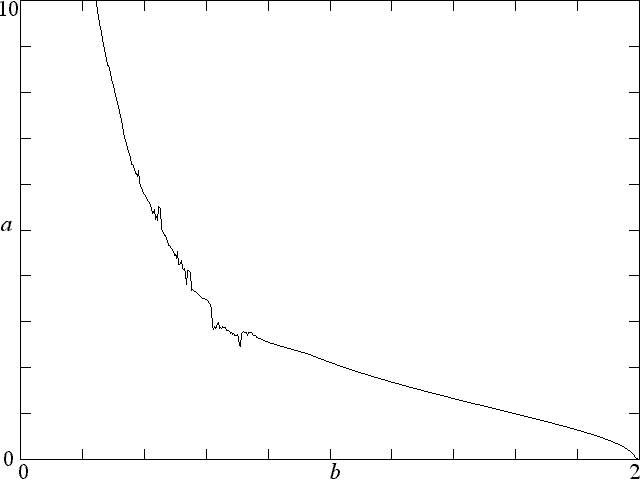
In the limit of large c, the behavior is independent of c, and the equation above can be written as
y''' + by'' + y' = a - exp(y)
where y = 2x and a = 2e. This system is thus governed by only the two parameters a and b, and the regions of chaos in ab space are shown below:

This system has an equilibrium point at x = ln a, y = 0, z = 0 that is stable for b > a and undergoes a Hopf bifurcation at b = a to a limit cycle with unit angular frequency.